
- •2.2. Конспект лекции Лекции № 1-3 Тема 1. Линейная алгебра
- •§ 1.1. Матрицы. Определители 2-го и 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
§ 2.2. Простейшие задачи аналитической геометрии
Рассмотрим две простейшие задачи: нахождение расстояния между двумя точками и деление отрезка в данном отношении.
Расстояние между точками A и B будем обозначать через AB. Оно обладает следующими свойствами.
AB
 0.
AB=0
только в том случае, когда A=B.
0.
AB=0
только в том случае, когда A=B.AB=BA.
AC≤AB+BC.
Теорема 1. Расстояние между точками A(xA) и B(xB) на оси Ox находится по формуле AB=xB–xA. Здесь справа записан модуль разности между координатами точек B и A.

Рис.2.3 Расстояние между точками
Теорема 2.
Расстояние между точками A(xA,yA)
и B(xB,yB)
на плоскости Oxy
находится по формуле
 .
.
Теорема 3.
Расстояние между точками A(xA,yA,zA)
и B(xB,yB,zB)
в пространстве
Oxyz
находится
по формуле
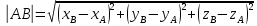 .
.
Пример. Пусть A(1,1,1), B(2,3,–1). Найдём |AB|.

Определение.
Разделить
отрезок
AB
в отношении
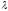
 это значит найти на нём такую точкуC,
что
это значит найти на нём такую точкуC,
что

Теорема 4.
Пусть точки A(xA)
и B(xB)
лежат на оси Ox
и точка C(xC)
делит отрезок AB
в отношении
 ,
тогда
,
тогда .
.
Доказательство. Пусть xBxA, тогда xAxCxB, |AC|=xC–xA, |MB|=xB–xC, из определения точки C получим уравнение:

Решим его.

Теорема 5.
Пусть точка
C(xC,yC,zC)
делит отрезок AB
в отношении

 ,
гдеA(xA,yA,zA),
B(xB,yB,zB),
тогда
,
гдеA(xA,yA,zA),
B(xB,yB,zB),
тогда

Пример2.
Найти координаты точки M,
делящей
отрезок AB
в отношении
 ,
гдеA(1,1,2),
B(4,7,8).
Получим:
,
гдеA(1,1,2),
B(4,7,8).
Получим:

Следовательно, M(2,3,4).
Следствие. Если точка M является серединой отрезка AB, то
 .
.
Эти формулы получаются из формул теоремы 5 при =1.
§ 2.3. Векторы и линейные операции над ними. Базис векторного
пространства. Координаты вектора
Векторы используются для описания величин имеющих определённое направление. Примерами таких величин являются сила, скорость, перемещение.
Определение.
Вектором
называется отрезок с выбранным
направлением, или направленный отрезок.
Вектор с
началом в точке
A и с концом
в точке B
обозначается через
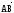 ,
кроме того
вектор можно обозначать одним символом,
например
,
кроме того
вектор можно обозначать одним символом,
например
 .
.
Вектор, у которого
начало совпадает с его концом
называется нулевым
вектором и обозначается через
 .
Длина отрезка, изображающего вектор
.
Длина отрезка, изображающего вектор ,
называетсямодулем
этого
вектора и обозначается |
,
называетсямодулем
этого
вектора и обозначается | |.
|.
Векторы
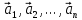 ,
параллельные одной прямой называютсяколлинеарными.
Нулевой вектор считается коллинеарным
любому вектору.
,
параллельные одной прямой называютсяколлинеарными.
Нулевой вектор считается коллинеарным
любому вектору.
Два вектора
 и
и считаютсяравными,
если они равны по модулю, коллинеарны
и одинаково направлены. Из этого
определения следует, что при параллельном
переносе вектор не меняется, по этому
в качестве начала вектора можно выбрать
любую точку.
считаютсяравными,
если они равны по модулю, коллинеарны
и одинаково направлены. Из этого
определения следует, что при параллельном
переносе вектор не меняется, по этому
в качестве начала вектора можно выбрать
любую точку.
Линейными операциями над векторами называются умножение вектора на число и сложение векторов.
Определение.
Произведением
вектора
 на число
называется такой вектор
на число
называется такой вектор  ,
что выполняются три условия.
,
что выполняются три условия.
|
 |=|||
|=||| |
|
 ||
||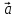
Вектор
 сонаправлен вектору
сонаправлен вектору
 ,
если0
и направлен в противоположную сторону,
если 0.
,
если0
и направлен в противоположную сторону,
если 0.
Пример1.
Ниже изображены вектора
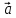 ;
0,5
;
0,5 ;
–2
;
–2 .
.

Рис. 2. 4 Умножения вектора на число
Определение.
Суммой
векторов
 и
и
исходящих из одной точки
называется вектор
совпадающий с диагональю параллелограмма,
образованного векторами
исходящих из одной точки
называется вектор
совпадающий с диагональю параллелограмма,
образованного векторами
 и
и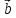
исходящий из той же точки.
исходящий из той же точки.

Рис. 2.5 Сложение векторов
Если вектора
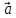 и
и не исходят из одной точки, то их начала
необходимо с помощью параллельного
переноса перенести в одну точку. Это
определение называетсяправилом
параллелограмма.
При сложении большого числа векторов
удобнее пользоваться следующим
определением, равносильным предыдущему.
не исходят из одной точки, то их начала
необходимо с помощью параллельного
переноса перенести в одну точку. Это
определение называетсяправилом
параллелограмма.
При сложении большого числа векторов
удобнее пользоваться следующим
определением, равносильным предыдущему.
Суммой векторов
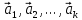
у которых начало
у которых начало
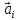 вектора совпадает с концом
вектора совпадает с концом (i=2k),
является вектор
соединяющий начало вектора
(i=2k),
является вектор
соединяющий начало вектора
 с концом вектора
с концом вектора .
.

Пример2.
Если вектора
 ,
, ,
, совпадают с тремя рёбрами параллелепипеда
исходящими из одной вершины, то их сумма
совпадают с тремя рёбрами параллелепипеда
исходящими из одной вершины, то их сумма +
+ +
+ совпадает с диагональю этого
параллелепипеда, исходящей из той же
вершины (рис.2.6)
совпадает с диагональю этого
параллелепипеда, исходящей из той же
вершины (рис.2.6)

Эти линейные операции над векторами обладают следующими свойствами.
1
 =
=
0
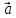 =
=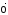
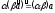


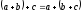

Операция разности
векторов
 и
и сводится к двум линейным операциям:
сводится к двум линейным операциям: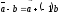 ,
однако часто удобней пользоваться
следующим специальным определением
равносильным вышеприведённому.
,
однако часто удобней пользоваться
следующим специальным определением
равносильным вышеприведённому.
Определение.
Разностью
векторов
 и
и ,
исходящих из одной точки называется
вектор, соединяющий конец вектора
,
исходящих из одной точки называется
вектор, соединяющий конец вектора с концом вектора
с концом вектора и направленный в сторону конца вектора
и направленный в сторону конца вектора .
.

