Свойства смешанного произведения.

I. Смешанное произведение векторов равнообъему параллелепипеда, построенного на этих векторах:

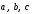
Здесь знак “+” берется в случае если тройка векторов  правая “” если она левая.

II. Векторы  являются компланарными только в том случае когда их смешанное произведение равно 0:

III. При перестановке местами любых двух векторов смешанного произведения оно меняет свой знак на противоположный; т.е.

IV. Постоянный сомножитель можно выносить из любого сомножителя смешанного произведения т.е. для любых векторов 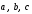и числа_: .

V. Смешанное произведение дистрибутивно для любого сомножителя т.е. для любых векторов верно: .

Получим теперь формулу позволяющую находить смешанное про изведение через координаты сомножителей.

Теорема. Пусть в базисе векторыимеют координаты соответственно и, тогда их смешанное произведение записывается в виде определителя:

.

Доказательство. Воспользуемся формулами, выражающими векторное и скалярное произведения через координаты сомножителей получим:

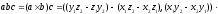
Пример. Проверим образуют ли векторы базис. Для этого вычислим их смешанное произведение по правилу Саррюса:

Поскольку 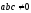, то эти векторы не компланарны т.е. они образуют базис в пространстве, т.к. , то этот базис – левый.

С помощью полученной формулы для смешанного произведения возможно вычисление объемов некоторых тел.

Следствие. Объем параллелепипеда построенного на векторах , равен:

.

Объем тетраэдра (треугольной пирамиды), образованного этими векторами равен:

.

Пример. Найдем объем тетраэдра с вершинами и.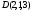

Данный тетраэдр образован векторами и, поэтому его объем равен:

.

Контрольные вопросы

1.В чем отличие скалярного произведения от векторного произведения векторов? Перечислите основные свойства скалярного и векторного произведений.

2. В чем заключается механический смысл скалярного произведения?

3. Что называется смешанным произведением?

4. В чем заключается геометрический смысл смешанного произведения?

5. Укажите условие коллинеарности двух векторов.

Литературы:

Основная [1] § 5,6,7 стр. 34-48

[19] 1.3-1.4, 1.10-1.13 стр. 12-20, 66-72, 83-87

Дополнительная

[30] Глава 2, § 1,2,3, стр. 41-75 Глава 3 § 1,2,3,4, стр. 76-93 Глава 4 § 1,2, стр. 94-109

Глава 5 § 1,2,3,4,5 стр. 110-142