§ 2.5. Скалярное произведение векторов и его свойства

Имеются три вида произведений векторов: скалярное, векторное и смешанное. Название первого из них произошло от слова скаляр – число. Скалярная величина в математике – это величина, принимающая численные значения.

Определение. Скалярным произведением векторов иназывается число, равное произведению модулей этих векторов на косинус угла между ними, т. е.

.

Скалярное произведение обозначается символами .

Пример 1. Если , то.

Пример 2. Пусть точка перемещается вдоль вектора под действием постоянной силы, составляющей уголс отрезком(см. рис. 2.15).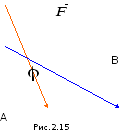

Тогда из механики известно, что работа этой силы по перемещению точки равна скалярному произведению векторов и, т.е.

.

Свойства скалярного произведения

1⁰ Для любых векторов и: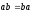, т.е. это произведение коммутативно.

2⁰ Для любого вектора :

. .

3⁰ Скалярные произведение ненулевых векторов 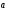иравнотолько в том случае, когда эти векторы ортогональны (перпендикулярны).

4⁰ Для любых векторов 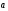иверно соотношение

.

5⁰ Для любого вектора с координатамив базисеверно

, ,.

6⁰ Постоянный множитель можно выносить за знак скалярного произведения, т.е. для любых векторов ,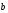и числаверно:

.

7⁰ Cкалярное произведение обладает свойством дистрибутивности, т.е. для любых векторов :.

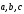Следствие.

Пример3. Найдем длину большей диагонали параллелограмма, образованного векторамии, если ,(см. рис. 2.16).

Поскольку 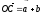, то

.

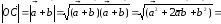
Получим формулу для вычисления скалярного произведения в случае, когда векторы заданы своими координатами, а также некоторые следствия из нее. Для определенности будем считать, что все векторы определены в пространстве. Для случая плоскости во всех формулах следует отбросить аппликаты всех векторов (координату ).

Теорема. Пусть в базисе векторимеет координаты, а вектор–. Тогда

.

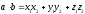Доказательство. Воспользуемся свойствами 6 и 7 скалярного произведения, получим

.

Поскольку базисные векторы 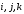взаимно перпендикулярны, то, а поскольку эти векторы имеют единичную длину, то. Подставив эти соотношения в последнее равенство, получим, что

.

Пример4. Если , а, то.

Следствие 1. Если вектор , в базисе, то

.

Доказательство. .

Пример5. Если , то

.

Следствие 2. Косинус угла 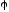между векторамииравен:

.

Доказательство. Из соотношения получим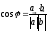. Затем для вычисления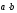воспользуемся теоремой, а дляи

следствием 1.

Пример6. Если ,, то

.

Следствие 3. Векторы иперпендикулярны только в том случае, когда

.

Определение. Направляющими косинусами ненулевого вектора называются косинусы углов, образованных этим вектором с осями координат (см. рис. 2.17).

Обычно эти углы обозначаются через .

Следствие 4. Для вектора с координатаминаправляющие косинусы записываются в виде:

;

;

.

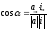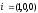Доказательство. Поскольку , то учитывая, чтоиз следствия 2 будем иметь:

.

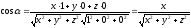Остальные формулы доказываются аналогично.

Пример 7. Если то

Направляющие косинусы вектора обладают следующим свойством.

Следствие 5.

Доказательство. Из предыдущего следствия получим:

Пример 7. Если то

Направляющие косинусы вектора обладают следующим свойством.

Следствие 5.

Доказательство. Из предыдущего следствия получим:

Определение. Вектор координаты которого совпадают с

направляющими косинусами вектора , называетсяортом вектора .

Его обозначение =().

Орт вектора по модулю равен 1 и сонаправлен вектору.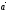

В самом деле из следствия и следует что 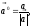т.е.коллинеарени имеет то же направление.

Пример 8. Для вектора :.