
Занятие 7 Уравнение прямой на плоскости
.docЗАНЯТИЕ 7
УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ
План:
-
Различные типы уравнений прямой на плоскости.
-
Связь между типами уравнений прямой на плоскости.
-
Взаимное расположение прямых на плоскости.
-
Угол между двумя прямыми.
-
Расстояние от точки до прямой.
Теоретические положения
Прямая линия на плоскости
Уравнение прямой с угловым коэффициентом. y= kx + b.
Общее уравнение прямой. Ах + Ву + С = 0
Уравнение прямой с заданным угловым коэффициентом и проходящей через данную точку. y-y1=k(x-х1).
Уравнение
прямой в отрезках.
![]()
Основные задачи на прямую
1. Составить уравнение произвольной прямой, проходящей через точку M1(x1;y1). Пусть уравнение искомой прямой
Ах + Ву + С = 0. (1)
Значит, M1 лежит на этой прямой. Поэтому
Ax1+By1 + C = 0. (2)
Вычитая из (1) почленно (2), получаем
A(x-x1)+B(y-y1)=0. (3)
Очевидно, при любых А и В уравнению (3) удовлетворяют координаты точки M1.
2. Составить уравнение прямой, проходящей через две данные (различные) точки M1(x1; y1) и M2(x2; у2). Уравнение прямой, проходящей через точку M1(x1;y1), имеет вид (3). Так как прямая проходит и через точку М2, то
А(х2-х1)+В(у2-у1) = 0, откуда
(4)
![]()
3. Угол между двумя прямыми. Рассмотрим на плоскости две прямые
l1(y = k1x + b1) и l2(y = k2x +b2) с углами наклона к оси Ох соответственно φ1 и φ2 (рис. 12).
![]()
4. Взаимное расположение двух прямых на плоскости. Если две прямые l1 и l2 лежат на плоскости, то возможны три различных случая их взаимного расположения:
1) пересекаются (т.е. имеют одну общую точку);
2) параллельны и не совпадают;
3) совпадают.
Если прямые l1 и l2 параллельны, то φ1 = φ2 и, следовательно, k1 = k2, т.е. параллельные прямые имеют равные угловые коэффициенты.
Пусть φ= π / 2 , т.е. l1 и l2 взаимно перпендикулярны. В этом случае k 2= - 1 / k 1
т. е. угловые коэффициенты взаимно перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.
Задания для работы в аудитории
-
Запишите уравнение прямой, проходящей через точку М(0;b) и имеющей угловой коэффициент k: а) М(0;2), k=1; б) М(0;0), k=-1.
-
Запишите уравнение прямой, проходящей через точку М (х0;у0) и имеющей угловой коэффициент k: а) М(1;1), k=2 ; б) М(-2;3), k=-4.
-
Составьте уравнение прямой, отсекающей на оси ординат отрезок а) b=3, и образующий с положительным направлением оси угол φ=π/4; б) b=3, и образующий с положительным направлением оси угол φ=3π/4.
-
Составьте уравнение прямой, проходящей через а) начало координат и точку А(-2;3); б) начало координат и точку В(2;-3).
-
Дано общее уравнение прямой -12х-5у-65=0. Напишите это уравнение в виде: а) уравнения прямой с угловым коэффициентом; б) уравнения прямой в отрезках.
-
Дано общее уравнение прямой 2х-3у-12=0. Напишите это уравнение в виде: а) уравнения прямой с угловым коэффициентом; б) уравнения прямой в отрезках.
-
Постройте прямые : а)
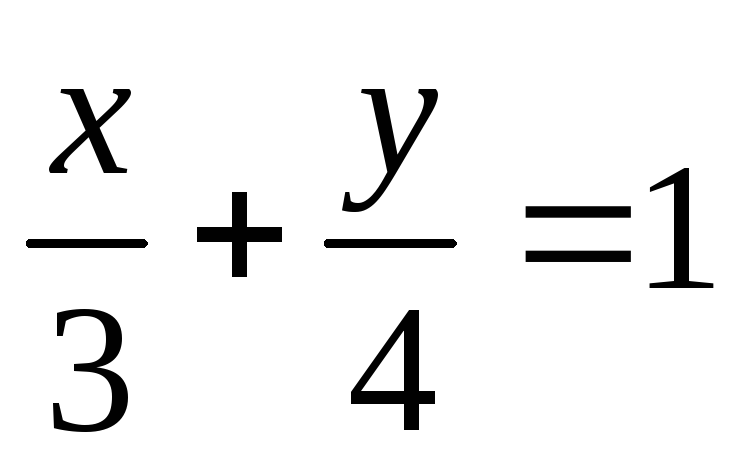 ;
б)
;
б)
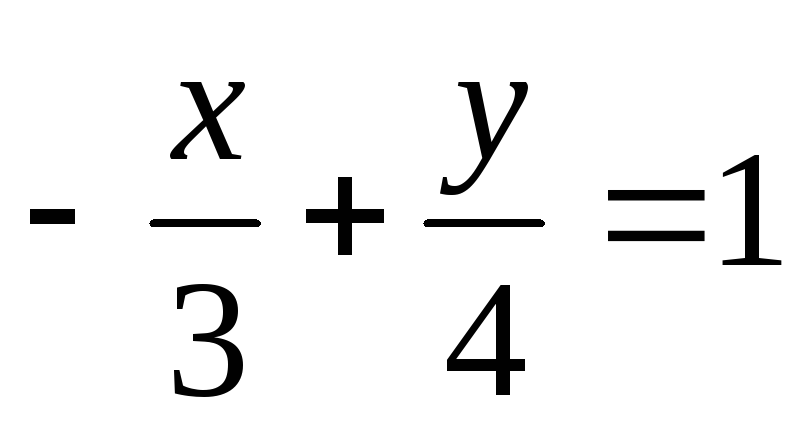 ;
в)
;
в)
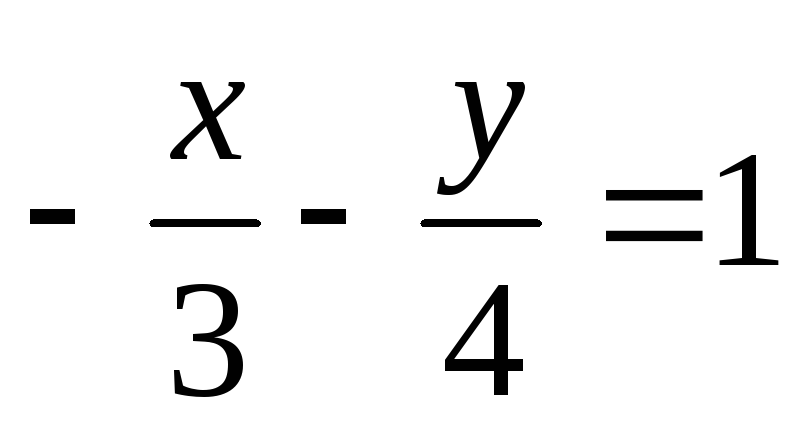 ;
г)
;
г)
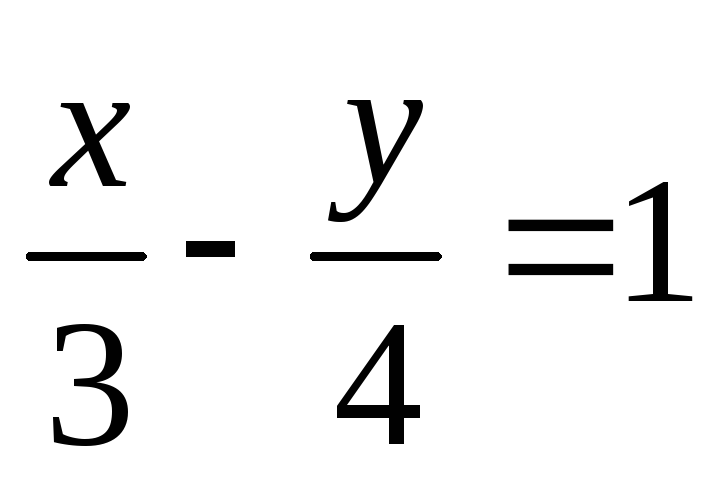 .
. -
Прямая проходит через точки А и В: а) А(0;2), В(5;0); б) А(-3;0), В(0;-2); в) А(0;1), В(-2;0). Напишите уравнение прямой в отрезках.
-
Параллельны ли прямые : а) 2х+3у-7=0 и 2х+3у+9=0; б) у=2х+3 и 4у-8х=1; в) х=3 и 10у+5=0?
-
Перпендикулярны ли прямые : а) 3х-5у+7=0 и 10х+6у-3=0; б) 2х-3у+11=0 и х+2у-1=0?
-
Напишите уравнение прямой, проходящей через точку А (2;3) и: а) параллельно прямой у=2х+5; б) перпендикулярно прямой у=2х+5.
-
Напишите уравнение прямой, проходящей через точку А (-1;2) и: а) параллельно прямой у=4х-7; б) перпендикулярно прямой у=4х-7.
-
Найдите координаты точки пересечения прямой 4х-3у-10=0 а) с осью Ох; б) с осью Оу.
-
Найдите координаты точки пересечения прямой 4х-3у-10=0 а) с осью Ох; б) с осью Оу.
-
Найдите точку пересечения двух прямых: а) 2х-4=0 и х-3у+1=0; б) 7х-9у+15=0 и 19х+12у-20=0.
-
Определите координаты вершин треугольника, если даны уравнения его сторон 2х+4у+1=0, х-у+2=0 и 3х+4у-12=0.
-
Даны уравнения сторон треугольника 2х-5у=3, х+3у=7 и 3х-2у+1=0. Напишите уравнение его высот.
-
Найдите угол между прямыми : а) у=- 2/5 х + 3 и у= 3/7 х +2/7; б) 6х+8у+5=0 и 2х-4у-3=0.
-
Под каким углом пересекаются прямые : а) х-2у-2=0 и у=
 ;
б) 3х+у-2=0 и х-3у+1=0; в) 4х-6у+7=0 и 20х-30у-11=0?
;
б) 3х+у-2=0 и х-3у+1=0; в) 4х-6у+7=0 и 20х-30у-11=0? -
Найдите расстояния от точек О(0;0), А(1;2), С(-2;1), К(-3;0) до прямой 3х-4у+10=0.
-
Даны уравнения сторон треугольника х-3у+5=0, 3х+4у+2=0 и 5х-2у-14=0. Найдите длины высот, опущенных на первые две указанных прямых, определяющих стороны треугольника.
-
Через точку пересечения двух прямых: 2х-у-3=0 и х-3у-4=0 проведена прямая, параллельная прямой х+у=1. Напишите уравнение проведенной прямой.
-
Через точку пересечения двух прямых: х+2у+2=0 и 3х+4у+9=0 проведен перпендикуляр к прямой 2х+3у-6=0. Напишите уравнение этого перпендикуляра.
-
Даны 2 стороны параллелограмма х-у+1=0 и 3х+2у-12=9 и точка К(6;4) – точка пересечения его диагоналей. Напишите уравнения двух других сторон параллелограмма.
-
Дано общее уравнение прямой 2х-3у + 6=0. Напишите это уравнение в виде: а) уравнения прямой с угловым коэффициентом; б) уравнения прямой в отрезках.
-
Определите длину отрезка прямой а)
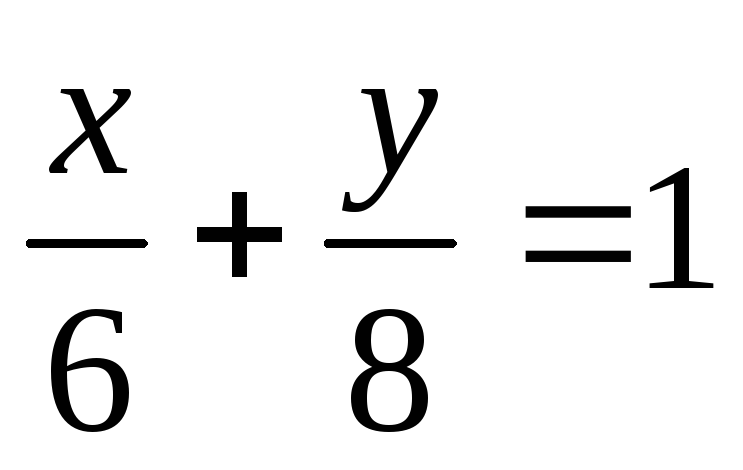 ,
заключенного между точками пересечения
прямой с осями координат.
,
заключенного между точками пересечения
прямой с осями координат.
Домашнее задание № 7
-
Составьте уравнение прямой, проходящей через точку А (2;5) и отсекающей на оси ординат отрезок b=7.
-
Составьте уравнения прямых, проходящих через стороны треугольника с вершинами А(1;3), В(0;2), С(-1;1). Постройте прямые.
-
Прямая проходит через точки А(0;1) и В(-2;0). Напишите уравнение прямой в отрезках.
-
Определите площадь треугольника, заключенного между осями координат и прямой
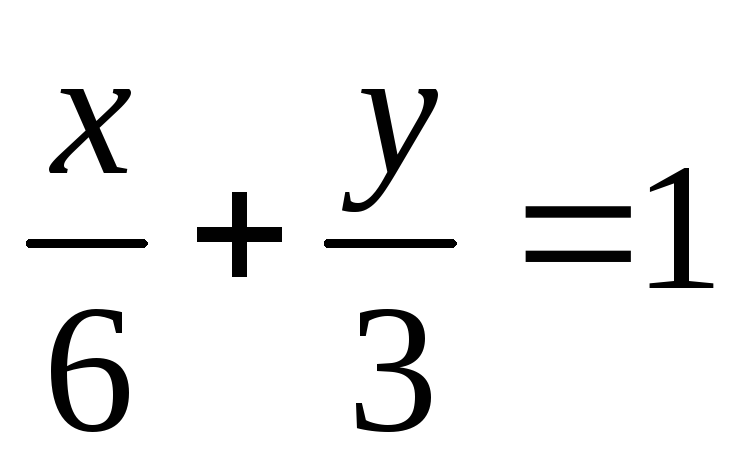 .
. -
Параллельны ли прямые : а) 3х-6у+4=0 и 5х-10у-1=0; б) у=х+1 и 2у-х=1; в) 3х-5у=0 и 6х+10у+5=0?
-
Перпендикулярны ли прямые : а) 3х-у-3=0 и х+3у-17=0; б) 2х+5у-6=0 и 5х+2у-3=0?
-
Напишите уравнение прямой, проходящей через точку А(-3;2) и а) параллельно прямой 7х+4у-11 =0; б) перпендикулярно прямой 7х+4у-11 =0.
-
Найдите координаты точки пересечения прямой 3х-4у+12=0 а) с осью Ох; б) с осью Оу.
-
Определите координаты вершин треугольника, если даны уравнения его сторон х-3у+11=0, 5х+2у-13=0 и 9х+7у-3=0.
-
Даны координаты вершин треугольника А(0;1), В(6;5) и С(12;-1). Напишите уравнения всех высот и медиан.
-
Под каким углом пересекаются прямые : а) у=3х+5 и у=-2х+7; б) 3х+у-7=0 и 2х-у+1=0?
-
Найдите расстояния от точек О(0;0), А(-1;1), С(2;-1) до прямой х-2у+1=0.
