математика

11

множителя табулированы.

Величину Р, полученную дисконтированием S, называют современной, или

текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалент-

ны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выпла- чиваемой в настоящий момент.

Пример. Сумма в 500 тыс. руб. выплачивается через 5 лет. Определить ее современную величину при условии, что применяется ставка сложных процен-

Если проценты начисляются m раз в году, то формула для расчета первона-

Банковский учет. В практике учетных операций иногда применяют слож- ную учетную ставку. Дисконтирование по сложной учетной ставке осуществля- ется по формуле:

При использовании сложной учетной ставки процесс дисконтирования про- исходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дис- конта.

Пример. Долговое обязательство на сумму 500 тыс. руб., срок оплаты кото- рого наступает через 5 лет, продано с дисконтом по сложной учетной ставке 15 % годовых. Каков размер полученной за долг суммы и величина дисконта?

Решение

P = 500(1− 0,15)5 = 221,853 тыс.руб.

Наращение по сложной учетной ставке. Иногда наращенную сумму по-

лучают и с помощью сложной учетной ставки. Из формул (3.11) следует:

При разработке условий финансовых операций часто сталкиваются с необ- ходимостью решения обратных задач — расчетом продолжительности договора

12

или уровня процентной ставки. Для получения соответствующих формул необ- ходимо решить уравнения (2.1) и (2.5), связывающие Р и S, относительно инте- ресующих нас величин.

Определение срока договора. При наращении по сложной годовой ставке i и

Пример. За какой срок в годах сумма, равная 75 тыс. руб. достигнет 200 тыс. руб. при начислении процентов по сложной ставке 15 % раз в году (m = 1) и поквартально (m = 4)?

Определение величины процентной ставки. Необходимые формулы для расчета ставок i, j при различных условий наращения процентов получим при решении уравнений, связывающих S и Р.

Пример. Сберегательный сертификат куплен за 100 тыс. руб., выкупная его цена 160 тыс. руб., срок 2,5 года. Каков уровень доходности инвестиций в виде годовой ставки сложных процентов?

Решение

i = 2,51,6 −1 = 0,2068 или 20,68 %.

Тема 3. Эквивалентность процентных ставок и финансовых обязательств

3.1. Эквивалентные процентные ставки

Эквивалентными называются процентные ставки, которые в конкретных ус- ловиях, т.е. в рамках одной финансовой операции приводят к одинаковым фи- нансовым результатам.

Если в финансовой операции размер процентной ставки изменяется во вре- мени, то все значения ставки можно обобщить с помощью средней. Замена всех

усредняемых значений ставок на среднюю процентную ставку по определению не изменяет результатов наращения или дисконтирования.

13

Простые процентные ставки. Пусть за последовательные периоды n1,…nk начисляются простые проценты по ставкам is1, … isk., тогда средняя ставка на- ращения будет:

где N = ån t — общее число периодов наращения процентов.

Найденный показатель представляет собой среднюю арифметическую взве- шенную с весами, равными продолжительности отдельных периодов.

Аналогичным способом определим среднюю учетную ставку:

Пример. Контракт предусматривает переменную по периодам ставку про- стых процентов: 20, 22 и 25 %. Продолжительность последовательных перио- дов начисления процентов: два, три и пять месяцев. Определить среднюю став- ку, которая приведет к аналогичному наращению исходной суммы?

Решение

= 2 × 0,2 + 3× 0,22 + 5× 0,25 =

is 0,231 или 23,1 % 10

Сложные процентные ставки. Если усредняются переменные во времени ставки сложных процентов, то из равенства множителей наращения следует:

Средняя ставка наращения в этом случае вычисляется как взвешенная средняя геометрическая.

Пример. Для первых двух лет ссуды применяется ставка, равная 15 % годо- вых, для следующих трех лет 20 % годовых. Определить среднюю ставку за весь срок договора.

Решение

i = 5(1+ 0,15)2 (1+ 0,2)3 −1 = 0,1797 , или 17,97 %.

Формулы эквивалентности ставок можно получить, исходя из равенства взя- тых попарно множителей наращения. Для этого следует применять формулы для определения наращенной суммы, с использованием различных ставок про- центов (ставок наращения и учетных ставок):

S = P(1+ nis )

S = P(1+ i)n

S = P(1+ j/ m)mn

S = P 1 1− nds

Пример. Вексель учтен за год до даты его погашения по простой учетной ставке 15 % годовых. Какова доходность учетной операции в виде простой процентной ставки?

Решение

Приравнивая множители наращения в формулах (4.4) и (4.7), получим:

Пример. Какой сложной годовой ставкой можно заменить в контракте про- стую ставку 18 % (К = 365), не изменяя финансовых последствий? Срок опера- ции 580 дней.

Решение

Приравниваем множители наращения в формулах (3.4) и (3.5).

1+ nis = (1+ i)n ; i = n1+ ni −1;

Пример. При разработке условий контракта стороны договорились о том, что доходность кредита должна составлять 24 % годовых. Каков должен быть размер номинальной ставки при начислении процентов ежемесячно (m = 12) и поквартально (m = 4)?

Решение

Необходимое соотношение получаем из равенства множителей наращения в формулах (3.5), (3.6).

(1+ i)n = (1+ j/ m)mn j = m(m1+ i −1)

j = 12(12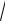1,24 −1) = 0,21705; или 21,705 %; j = 4(4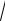1,24 −1) = 0,22100; или 22,1 %;

Для каждой из рассмотренных ставок можно получить по четыре соотноше- ния эквивалентности. Формулы для расчета эквивалентных ставок представле- ны в таблице 3.1.

Таблица 3.1. Эквивалентные процентные ставки

15

3.2. Финансовая эквивалентность обязательств

На практике нередко возникают случаи, когда необходимо заменить одно де- нежное обязательство другим, например с более отдаленным сроком платежа, объединить несколько платежей в один (консолидировать платежи) и т.п. Ясно, что такие изменения не могут быть произвольными. Неизбежно возникает во- прос о принципе, на котором должны базироваться изменения условий кон- трактов. Таким общепринятым принципом является финансовая эквивалент- ность обязательств.

Эквивалентными считаются такие платежи, которые, будучи "приведенны- ми" к одному моменту времени, оказываются равными. «Приведение» осуще- ствляется путем дисконтирования (приведение к более ранней дате) или, на- оборот, наращения суммы платежа (если эта дата относится к будущему). Если при изменении условий контракта принцип финансовой эквивалентности не со- блюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить.

На принципе эквивалентности основывается сравнение разновременных платежей. Покажем это на примере. Две суммы денег S1 и S2 выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. Замена S1 на S2 в этих условиях формально не изменяет отношения сторон.

Пример. Имеются два обязательства. Условия первого: выплатить 400 тыс. руб. через 4 месяца, условия второго: выплатить 450 тыс. руб. через 8 месяцев. Можно ли считать их равноценными? При дисконтировании на начало срока применить простую ставку, равную, 20 % годовых.

Решение

Используя формулу дисконтирования по простой процентной ставке (2.7), получим:

лентными при заданной ставке и в силу этого не могут адекватно заменять друг друга. Сумму, эквивалентную, например, первому платежу, но отнесенную к моменту выплаты второго (8 месяцев), можно найти путем наращения первого платежа:

P = 400(1+ 124 × 0,2) = 427,667 тыс.руб.

Если при сравнении разновременных платежей используется ставка слож- ных процентов, то дисконтирование осуществляется по формуле (2.9).

Пример. Имеются два обязательства. Условия первого: выплатить 100 тыс. руб. через 2 года, условия второго: выплатить 115 тыс. руб. через 4 года Можно ли считать их равноценными? При дисконтировании на начало срока приме- нить сложную ставку процентов, равную 12 % годовых.

Решение

P1 ¹ P2 , следовательно, платежи неэквивалентны. Сумму, эквивалентную пла-

тежу в 100 тыс. руб., но отнесенную к концу четвертого года, найдем путем на- ращения первого платежа:

P = 100(1+ 0,2)2 = 125,440 тыс.руб.

Как уже было сказано выше, принцип финансовой эквивалентности плате- жей применяется при различных изменениях условий выплат денежных сумм: их объединении, изменении сроков (досрочном погашении задолженности или, наоборот, пролонгировании срока) и т.п. Общий метод решения подобного рода задач заключается в разработке уравнения эквивалентности.

Уравнение эквивалентности это уравнение, в котором сумма заменяемых платежей, приведенных к какому-либо моменту времени, приравнивается к сумме платежей по новому обязательству, приведенных к тому же моменту времени.

Для краткосрочных обязательств приведение осуществляется обычно на ос- нове простых ставок, для средне- и долгосрочных — с помощью сложных про- центных ставок.

Одним из распространенных случаев изменения условий контрактов являет- ся консолидирование (объединение) платежей. Пусть платежи S1, …., Sm со сро- ками n1, ..., nm заменяются одним в сумме S0 и сроком n0. В этом случае воз- можны две постановки задачи: если задается срок n0 то находится сумма S0 и наоборот, если задана сумма консолидированного платежа S0, то определяется

17

срок n0. Рассмотрим обе постановки задачи.

Определение размера консолидированного платежа. В общем случае, ко-

гда n1 < n2 < … < nm, искомую величину находим как сумму наращенных и дис- контированных к моменту оплаты платежей.

Простая ставка процентов. При применении простых процентных ставок получим

где Sj — размеры объединяемых платежей со сроками nj < n0, Sk — размеры платежей со сроками nk > n0.

Пример. Два платежа 100 и 50 тыс. руб. со сроками уплаты соответственно 150 и 180 дней объединяются в один со сроком 200 дней. При конверсии при-

Пример. Изменим условия договора. Пусть теперь объединяющий платеж

Сложная ставка процентов. В случае долгосрочных договоров консолида- цию платежей осуществляют на основе сложных процентных ставок. Вместо (4.9) для общего случая (n1 < n0 < nm) получим

где также Sj — размеры объединяемых платежей со сроками nj < n0, Sk — раз- меры платежей со сроками nk > n0.

Пример. Платежи в 100 и 200 тыс. руб. и сроками уплаты через 2 и 3 года объединяются в один со сроком 2,5 года. При консолидации используется сложная ставка 20 %.

Определение срока консолидированного платежа. Если при объединении платежей задана величина консолидированного платежа S0, то возникает про- блема определения его срока n0. В этом случае уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствую-

18

щих платежей.

Простая ставка процентов. При применении простой ставки это равенство имеет вид:

где Ps – сумма современных стоимостей объединяемых платежей, определяемая по формуле:

S0 > åSj (1+ n ji)−1 , иначе говоря, размер заменяющего платежа не может быть

j

меньше суммы современных стоимостей заменяемых платежей. Заметим также, что искомый срок пропорционален величине консолидированного платежа.

Пример. Суммы в размере 10, 20 и 15 тыс. руб. должны быть выплачены че- рез 50, 80 и 150 дней соответственно. Стороны согласились заменить их одним платежом 45 тыс. руб. Определить срок выплаты заменяющего платежа. При сравнении платежей применяется ставка простых процентов 10 % годовых (К =

Сложная ставка процентов. В случае применения ставки сложных про- центов уравнение эквивалентности запишется следующим образом:

19

Пример. Платежи в 100 и 200 тыс. руб. и сроками уплаты через 2 и 3 года объединяются в один, размером 300 тыс. руб. Определить срок консолидиро- ванного платежа. При консолидации используется сложная ставка 20 % годо- вых.

Обсудим теперь общие случаи изменения условий выплат, предусматривае- мых в контрактах, для которых решение нельзя получить простым суммирова- нием приведенных на некоторую дату платежей. Разумеется, и в таких случаях решение основывается на принципе эквивалентности платежей до и после из- менения условий. Метод решения заключается в разработке соответствующего уравнения эквивалентности. Если приведение платежей осуществляется на не- которую начальную дату, то получим следующие уравнения эквивалентности в общем виде:

Здесь Sj, и nj, — параметры заменяемых платежей, Sk и nk — параметры заме- няющих платежей.

Конкретный вид равенства определяется содержанием контрактов, поэтому методику разработки уравнений эквивалентности удобнее показать на приме- рах. Для этого рассмотрим два примера.

Пример. Имеется обязательство уплатить 100 тыс. руб. через 4 месяца и 70 тыс. руб. через 8 месяцев после некоторой даты. По новому обязательству не- обходимо выплату произвести равными суммами через 3 и 9 месяцев. Измене- ние условий осуществляется с использованием простой ставки, равной 10 %.

Решение

Примем в качестве базовой даты начало отсчета времени. Уравнение экви- валентности в этом случае записывается следующим образом:

Из решения уравнения получим: S = 85,204 тыс. руб.

Пример. Существует обязательство уплатить 100 тыс. руб. через 5 лет. Сто-

20

роны согласились изменить условия погашения долга следующим образом: че- рез два года выплачивается 30 тыс., а оставшийся долг — спустя 6 лет после начала договора. На долг начисляются сложные проценты по ставке 10 % годо- вых. Определить сумму последнего платежа.

Решение

В этом случае уравнение эквивалентности удобно составить на момент по- следнего платежа (на конец шестого года).

100(1+ 0,1) = 30(1+ 0,1)4 + S.

Откуда получаем S = 66,077 тыс.руб.

Тема 4. Учет инфляции в финансовых расчетах

В рассмотренных выше методах определения наращенной суммы все денеж- ные величины измерялись по номиналу. Иначе говоря, не принималось во вни- мание снижение реальной покупательной способности денег за период, охваты- ваемый операцией. Однако в современных условиях инфляция в денежных от- ношениях играет заметную роль, и без ее учета конечные результаты часто представляют собой условную величину.

Инфляцию необходимо учитывать, по крайней мере, в двух случаях: при

расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой операции. Остановимся на этих проблемах. Введем следующие обозначения:

S — наращенная сумма денег, измеренная по номиналу;

С — наращенная сумма с учетом ее обесценивания за счет инфляции;

JP — индекс цен, величина, показывающая, во сколько раз возросли цены за анализируемый период; α – темп инфляции (относительный прирост цен за анализируемый период);

r – номинальная ставка процента; i – эффективная ставка процента.

Очевидно, что

Пусть, например, сегодня получено 150 тыс. руб. Известно, что за два пред- шествующих года цены увеличились в 1,5 раза (или повышение на 50 %), JP =1,5. Следовательно, реальная покупательная способность 150 тыс. руб. со- ставит 150/1,5 = 100 тыс. руб. в деньгах с покупательной способностью двух- летней давности.

Индекс цен определяется темпом инфляции:

Например, если темп инфляции за период равен 30 %, то это означает, что цены выросли в 1,3 раза.

Инфляция является цепным процессом. Следовательно, индекс цен за не- сколько периодов равен произведению индексов цен за каждый период. Если инфляция постоянна на протяжении нескольких периодов времени ( α = const ), то индекс цен за n периодов (месяцев, лет и т.д.) определяется по формуле: