I уровень

1.1.Найдите функцию, обратную данной, если она существует:

1) 2)3)

4) 5)6)

1.2.Докажите, что пары функций являются взаимно-обрат­ными:

1)иесли

2)и

3)и

4)иесли

1.3.Постройте график функции и ей обратной (если она существует) в одной системе координат:

1) если2)

3)4)если

1.4.Найдите точку (точки), принадлежащую кривой для заданного значениях₀:

1)

2)

3)

1.5.Запишите функцию (функции) в явном виде:

1) 2)

3) 4)

1.6. Найдите соответствующие точки кривой, заданной параметрически, если указаны значения параметраt:

1) 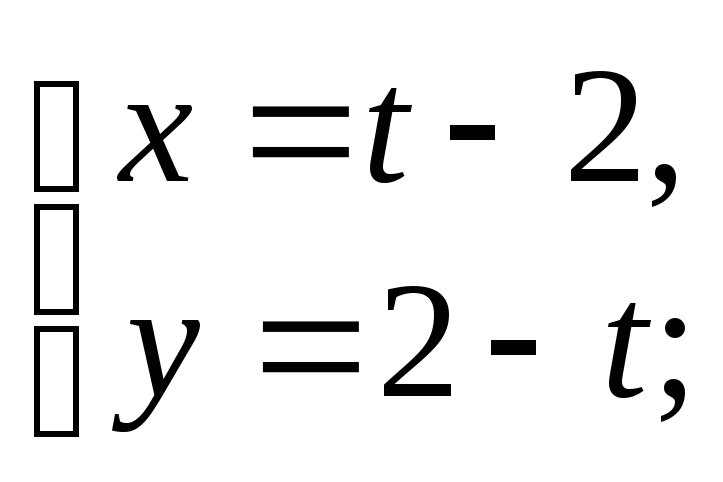2)3)

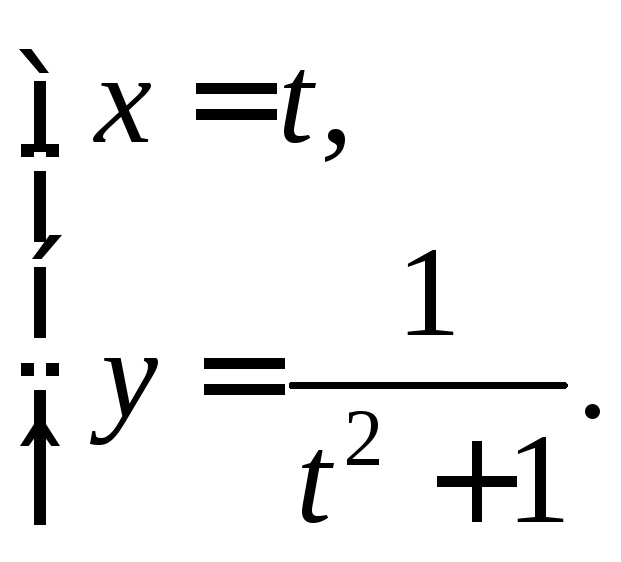
II уровень

2.1.Найдите функцию, обратную данной, и постройте их графики в одной системе координат:

1) 2)

3) 4)

5) 6)

2.2. Определите, обратима ли функция

2.3. Найдите точки пересечения графиков функциигдеи обратной ей функции.

2.4.Пусть графиком функции является полуокружность с центромО(0; 0) и радиусом, равным 5, расположенная в нижней координатной полуплоскости. Определите, существует ли функция, обратная данной.

2.5.Пусть задана функция

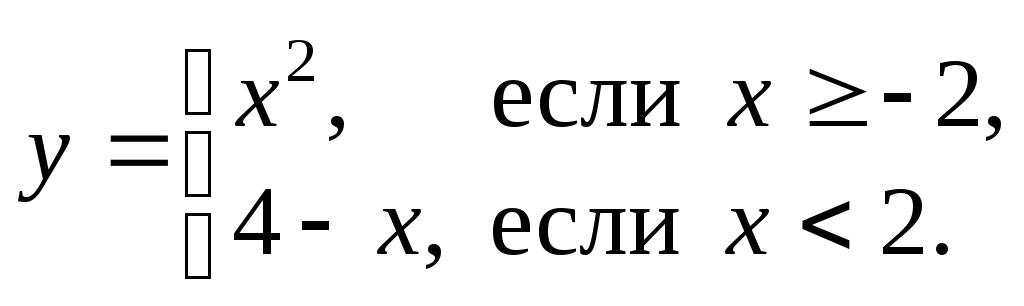
Найдите промежутки, на которых данная функция обратима.

2.6.Выразите явноучерезхиз уравнения и постройте данную линию:

1)

2) если

3) если

4) если

2.7.Постройте линию, заданную параметрически уравнениями:

1) 2)

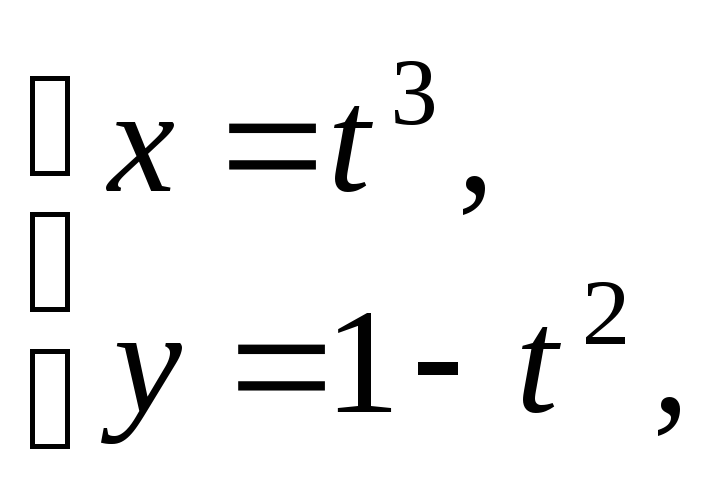
3) 4)

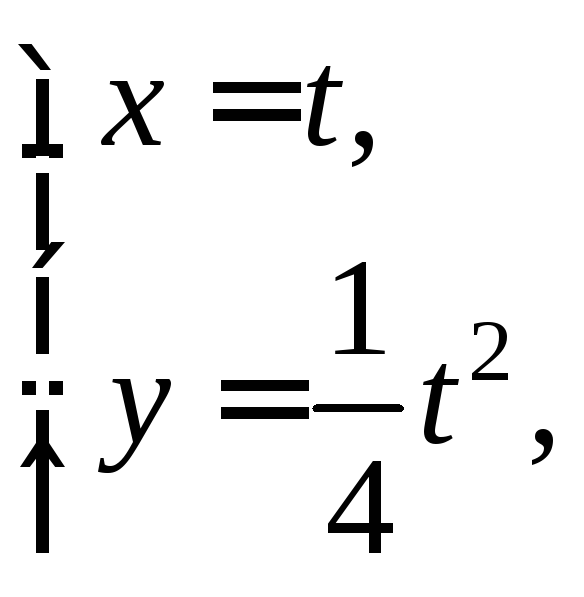
III уровень

3.1. Найдите функцию, обратную данной, и постройте их графики в одной системе координат:

1) 2)

3) 4)

5) 6)

3.2.Докажите, что функцияобратна сама себе.

3.3.Найдитеесли функцияобратна функции

4.3. Преобразования графиков

Приведем графики некоторых функций:

1) – прямая линия (рис. 4.7);

2) – квадратичная парабола (рис. 4.8);

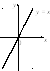
Рис. 4.7 Рис. 4.8

3) – кубическая парабола (рис. 4.9);

4) – гипербола (рис. 4.10);

Рис. 4.9 Рис. 4.10

5) – график квадратного корня (рис. 4.11).

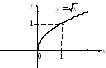
Рис. 4.11

Правила преобразования графиков:

Пусть дана функция

1. Для построения графика функции исходный график функциисимметрично отображаем относительно осиОх(рис. 4.12).

2. Для функции заданный график симметрично отображаем относительно осиОу(рис. 4.13).

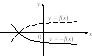
Рис. 4.12 Рис. 4.13

3. Для функции этот график получается параллельным переносом графика функциинамасштабных единиц вдоль осиОувверх, еслии вниз, если(рис. 4.14).

4. Для функции этот график получается параллельным переносом графика функциинамасштабных единиц вдоль осиОхвправо, еслии влево, если(рис. 4.15).

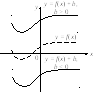
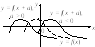
Рис. 4.14 Рис. 4.15

5. Для функции гдеграфик функции«растянут» в kраз вдоль осиОу(от осиОх), если«сжат» в раз вдоль осиОу (к оси Ох), если (рис. 4.16).

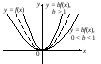
Рис. 4.16

6. Для функции гдеграфик«растянут» вдоль осиОх(от осиОу) враз при«сжат» вдольОх(к осиОу) вmраз, при(рис. 4.17).

Рис. 4.17

7. Для функции сохраняется та часть графика функциикоторая находится над осьюОхи на осиОх, а та часть, которая находится под осьюОх, отображается симметрично осиОхв верхнюю полуплоскость (рис. 4.18).

Рис. 4.18

8. Для функции часть графика функциисоответствующая отрицательному значениюх, отбрасывается, а неотрицательному – сохраняется и дополняется симметричной ей относительно осиОучастью (рис. 4.19).

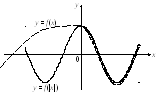
Рис. 4.19

Пример 1. Построить график функции

Решение. Преобразуем заданную функцию:

Получили

Для построения графика полученной функции используем следующие преобразования:

1. строим график функции

2. график функции 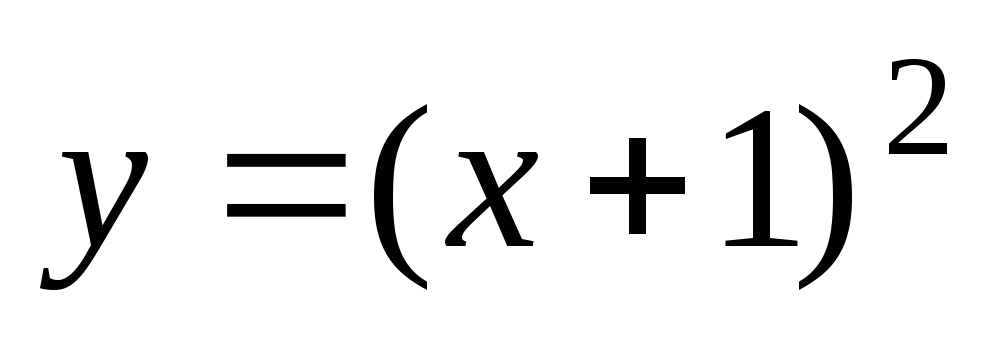получаем из графика функции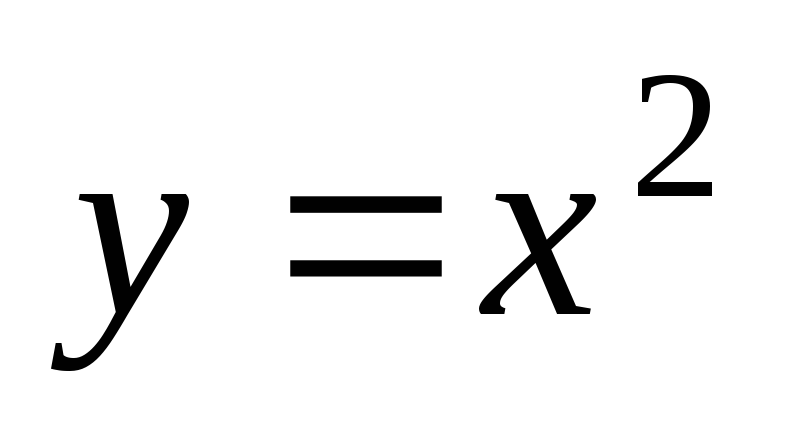путем движения его на единицу влево по осиОх;

3. график функции 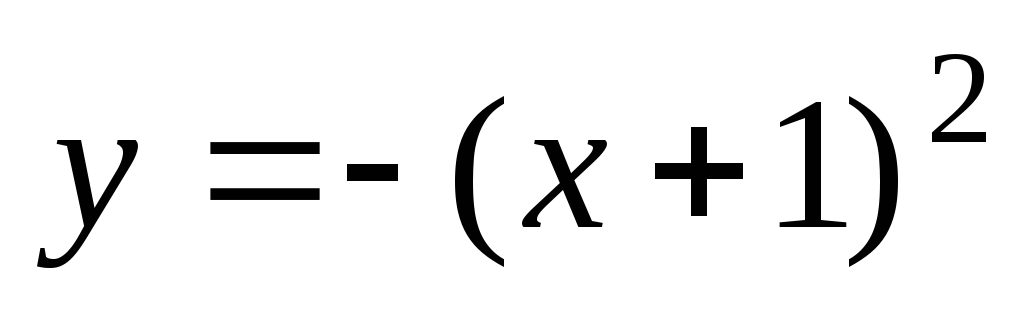получаем из предыдущего симметричным отображением относительно осиОх;

4. график заданной функции получаем из графика функции параллельным переносом на две единицы вниз по осиОу (рис. 4.20).

Рис. 4.20

Пример 2. Построить график функции

Решение. Вначале преобразуем формулу, задающую функцию:

Шаги построения (рис. 4.21):

1)

2) – отображение симметрично осиОу в левую полуплоскость;

3) – смещение вдоль осиОх вправо на две единицы;

4) – увеличение коэффициента роста в два раза.

Рис. 4.21

Пример 3. Построить график функции и найти наибольшее значение функции, если

Решение.

Преобразуем функцию

Данный график может быть получен из графика функции следующими преобразованиями (рис. 4.22):

1) – смещение вдоль осиОх на единицу влево;

2) – смещение вдоль осиОу вверх на единицу;

3) – отображение той части графикау₃, которая расположена ниже оси Ох, в верхнюю полуплоскость (рис. 4.22). Заметим, что такие же преобразования необходимо применить к асимптотам функции (вертикальной) и(горизонтальной).

Анализ графика показывает, что наибольшее значение на функция достигает в точкеВычисляем его:

Рис. 4.22

Пример 4. Определить, при каком значении а уравнение имеет ровно 3 решения:

Решение. Решим задачу графически.

Построим графики функций ии исследуем, при каком значенииа они имеют ровно 3 общие точки.

Строим график функции

Поскольку то

–это парабола, вершина которой смещена в точку

Для построения графика функции сохраняем ту часть графика параболы, которая находится над осьюОх и на оси Ох, а ту часть графика, которая находится под осью Ох, отображаем симметрично оси Ох в верхнюю полуплоскость.

–прямая, параллельная оси Ох (рис. 4.23).

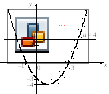
Рис. 4.23

По построению видно, что ровно 3 решения будет тогда и только тогда, когда

Задания