5. Степени и корни

5.1. Корень n-й степени

Для всякого числа a  R определена степень с натуральным показателем aⁿ, n  N.

Число b  R называется корнем n-й степени, n  N, n  2, из числа а, если обозначают

Нахождение корня n-й степени из данного числа а называют извлечением корня n-й степени из числа а. Число а, из которого извлекается корень n-й степени, называют подкоренным выражением, а число n – показателем корня.

Если тоопределен для всехa  R и принимает любые действительные значения.

Если тоопределен для всехa  0 (a  R). В курсе элементарной математики рассматривают арифметическое значение корня, т. е. число

Свойства корней

Пусть a, b  R, тогда:

1)

2)

3)

4)

5)

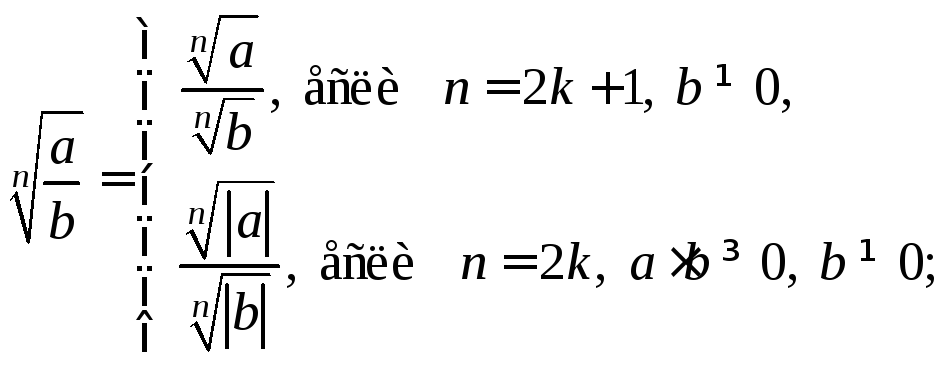
6) гдеa  0 в случае

7) гдев случае

8) гдев случае

Пример 1. Вычислить

Решение. 1-й способ. Выделим полные квадраты подкоренных выражений:

Тогда получим

2-й способ. Обозначим вычисляемое выражение через a, т. е.

Заметим, что

Возведем обе части полученного равенства в квадрат:

Тогда

Поскольку исходное выражение положительно, в ответе получаем a = 4.

Пример 2. Упростить выражение

Решение. 1-й способ. Используем формулы квадрата разности и суммы, а также свойства корней. Получаем:

2-й способ. При упрощении иррациональных выражений часто бывает эффективным метод рационализации, основанный на замене переменных.

Введем такую замену переменных, чтобы корни извлеклись:

Заданное выражение приобретает вид

Упрощаем его, используя формулы сокращенного умножения:

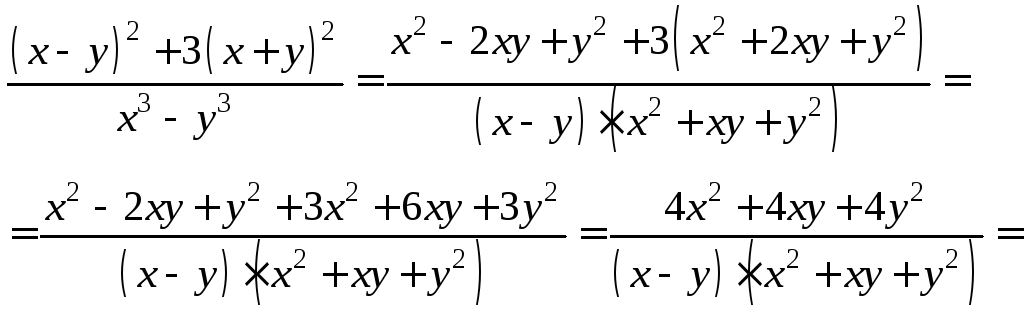
Возвращаясь к старым переменным, приходим к ответу

Пример 3. Избавиться от иррациональности в знаменателе:

1) 2)3)

Решение. 1) Умножим числитель и знаменатель дважды на сопряженные выражения и воспользуемся формулой разности квадратов:

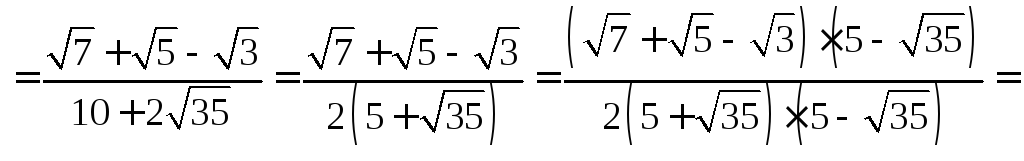
2) Домножим числитель и знаменатель на неполный квадрат разности и воспользуемся формулой суммы кубов:

3) Умножим числитель и знаменатель дважды на сопряженные выражения:

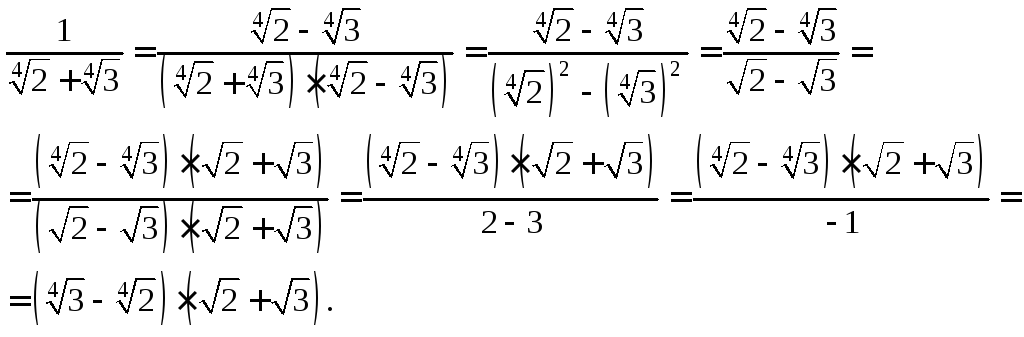
Задания

I уровень

1.1. Вычислите значения корней:

1) 2)3)4)

5) 6)7)8)

9) 10)11)12)

13) 14)15)

1.2. Сравните числа:

1) и2)и3)и

4) и5)и6)и

7) и8)и 1; 9)и

10) и11) 3 и12)и

13) и14)и

1.3. Избавьтесь от иррациональности в знаменателе:

1) 2)3)4)

5) 6)7)8)

9) 10)11)

1.4. Упростите выражение:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

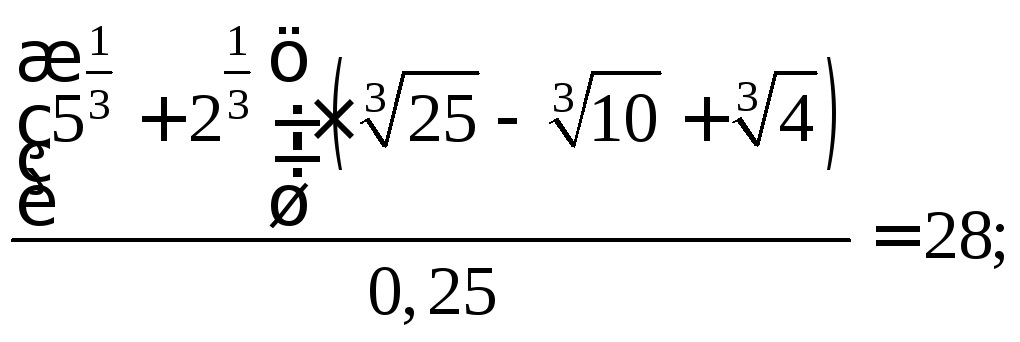
14)

15)

II уровень

2.1. Упростите выражение:

1)

2)

3)

4)

5)

6)

7)

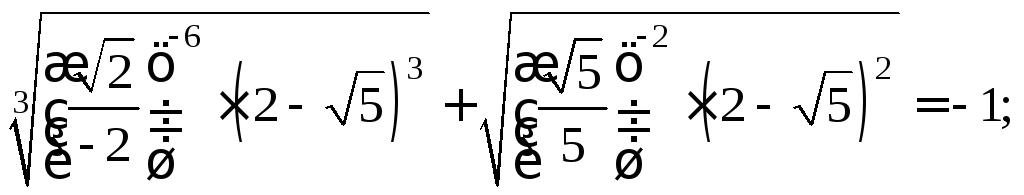
8)

9)

2.2. Избавьтесь от иррациональности в знаменателе:

1) 2)3)

4) 5)6)

7) 8)9)

10) 11)12)

2.3. Упростите выражение:

1)

2)

3)

4)

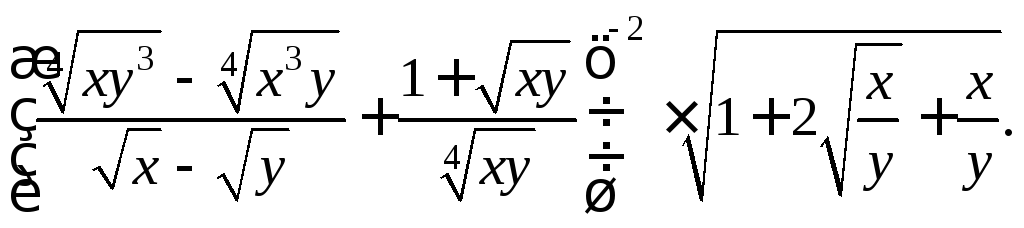
III уровень

3.1. Избавьтесь от иррациональности в знаменателе:

1) 2)3)

4) 5)6)

7) 8)9)

10) 11) 12)

13)

3.2. Упростите выражение:

1) 2)

3) 4)

5) 6)

7) 8)

9)

10)

Степень с произвольным действительным

показателем

Во множестве R определена степень a^x с действительным показателем.

В выражении a^x число а называют основанием степени, число x – показателем степени. Нахождение значения степени называют возведением в степень.

Степень с действительным показателем

Пусть a  R, тогда:

1) n  N;

2)

3)

4) иa  0, если

5) и еслито a  0;

6) и

На множестве R не определены отрицательная и нулевая степень числа 0, а также если

Свойства степеней

Допустим, что a, b, c  R и это такие числа, что все степени имеют смысл. Тогда:

1)

2)

3)

4)

5)

6) если a > 1 и x < y, то

если 0 < a < 1 и x < y, то

7) если 0 < a < b и x >0, то

если 0 < a < b и x < 0, то

Пример 1. Вычислить

Решение. Используем свойства степеней

Пришли к ответу:

1.2. Выполните действия:

1) 2)3)

4) 5)6)

7) 8)

9)

1.3. Найдите из уравнения:

1) 2)3)

4) 5)6)

1.4. Упростите выражение