11.3. Уравнение касательной

и нормали. Физический смысл производной

Производная функции в точкепредставляет собой угловой коэффициент касательной, проведенной к графику функции в точке

где – угол наклона касательной к осиOx. В этом состоит геометрический смысл производной.

Уравнение касательной, проведенной к графику функции в точке гдеимеет вид:

(11.9)

Прямая, проходящая через точку графика функцииперпендикулярно касательной, проведенной в этой точке, называетсянормалью к графику функции в точке(рис. 11.1). Уравнение нормали имеет вид:

(11.10)

где

Рис. 11.1

Физические приложения производной

1. Если материальная точка M движется неравномерно по пути, заданному функцией томгновенная скорость движения в момент времени есть производная от путиS по времени t:

(11.11)

2. Если функцией описывается процесс изменения скорости неравномерного движения в зависимости от времени, то мгновенное ускорение материальной точки в момент времени есть производная от скоростиv по времени t:

(11.12)

3. Если – функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до температурыT, то теплоемкость тела есть производная от количества теплоты Q по температуре T:

4. Линейная плотность неоднородного тонкого стержня в точке есть производная от массыm по длине l:

5. Мгновенное значение электродвижущей силы индукции равно скорости изменения магнитного потока, т. е. производной от магнитного потока  по времени t:

6. Сила тока в колебательном контуре в момент времени t₀ равна производной заряда q по времени t:

Пример 1. Написать уравнение касательной и нормали, проведенной к графику функции в точке с абсциссойx = 2.

Решение. Для нахождения уравнения касательной воспользуемся формулой (11.9). Сначала найдем ординату точки касания Для этого значениеподставим в уравнение функции:

Для нахождения углового коэффициента найдем производную используя формулу дифференцирования дроби:

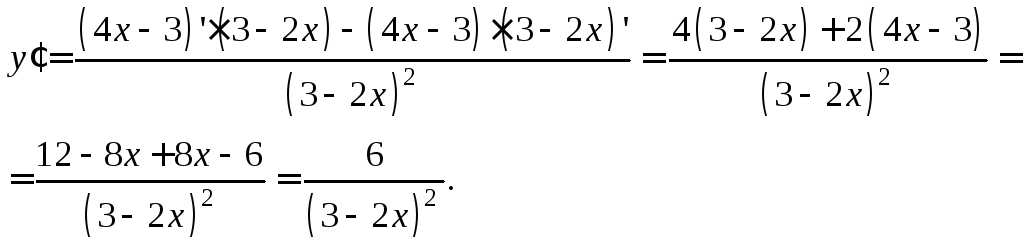
Найдем значение производной при

Подставив найденные значения в формулу (11.9), получаем уравнение касательной:

т. е.

Чтобы написать уравнение нормали, воспользуемся формулой (11.10):

Получим, что уравнение нормали, проведенной к заданной кривой в заданной точке, имеет вид

Пример 2. Определить, в какой точке кривой касательная наклонена к оси абсцисс под углом 45.

Решение. Так как тангенс угла наклона касательной к оси абсцисс равен значению производной в точке касания, найдем производную функции:

По условию Следовательно,

Отсюда:

Получили два значения абсциссы точки касания:

т. е. существуют две точки касания, в которых касательная образует угол 45 с осью Ох.

Найдем соответствующие ординаты точек касания, подставляя значения в формулу функции:

Приходим к ответу: в точках икасательная к заданной кривой образует с осьюОх угол 45.

Пример 3. Найти острый угол между параболами ив точке их пересечения, имеющей отрицательную абсциссу.

Решение. Угол между двумя кривыми в точке их пересечения – это угол между касательными к этим кривым, проведенными в точке их пересечения. Тангенс этого угла вычислим по формуле

(11.13)

где k₁ и k₂ – угловые коэффициенты касательных, проведенных к параболам в заданной точке.

Найдем точку пересечения этих парабол. Для этого решим систему:

Отсюда Условию задачи удовлетворяет точкаНайдем коэффициентk₁:

Аналогично найдем k₂:

Воспользуемся формулой (11.13) и получим:

откуда

Пример 4. Тело движется прямолинейно по закону

Найти скорость движения тела в тот момент, когда ускорение равно нулю.

Решение. Согласно формуле (11.11), скорость есть производная функции S(t), а, согласно формуле (11.12), ускорение а(t) есть производная скорости v(t).

Последовательно вычислим производные:

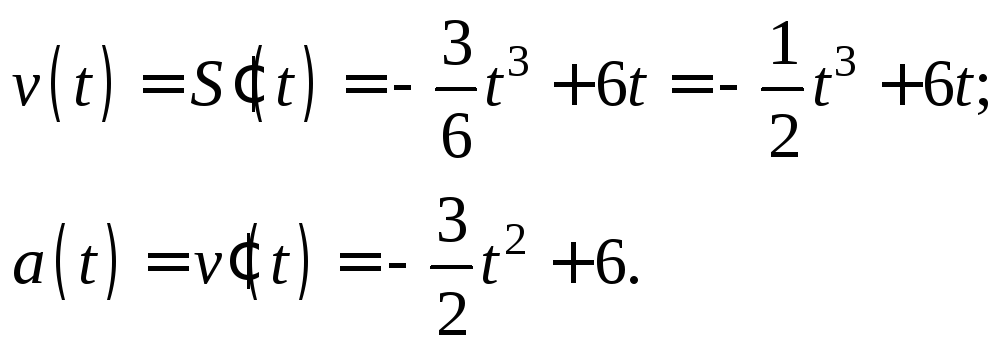
Найдем момент времени, когда ускорение равно нулю:

Вычислим скорость движения тела в момент времени

Задания