II уровень

2.1. Найдите производную предварительно преобразовав выражение:

1) 2)

3) 4)

2.2. Для функции найдите

2.3. Известно, что Найдите

2.4. Решите неравенство где

III уровень

3.1. Вычислите если:

1)

2)

3.2. Пользуясь определением производной, найдите если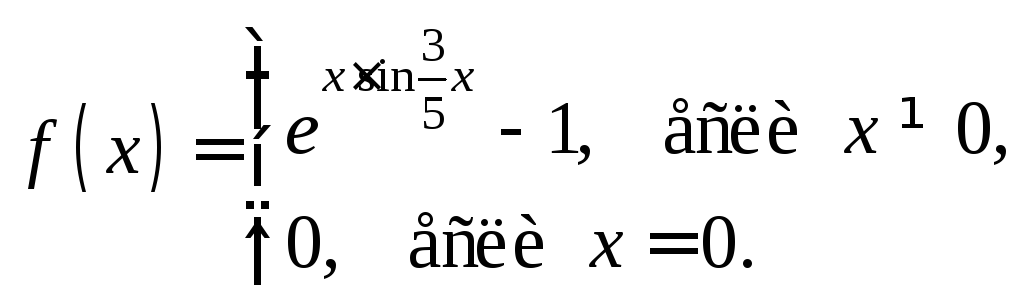

3.3. Найдите значение производной функции в точке если

3.4. Найдите сумму значений производной функции у(х) в точках x = 1 и x = 0, если

11.2. Производная сложной функции

Если и– дифференцируемые функции своих аргументов, то производная сложной функции вычисляется по формуле

(11.8)

Обобщенная таблица производных

где в частности:

где в частности,

где в частности,

Если для функции y = f(x) существует обратная функция x = (y), которая имеет производную то верна формула

(11.9)

Пример 1. Найти производную функции:

1) 2)

3) 4)

5) 6)

Решение. 1) Функцию необходимо рассматривать как сложную функцию, гдеи– дифференцируемые функции своих аргументов. Тогда, согласно формуле (11.8) и соответствующим формулам таблицы производных, получим:

2) Сначала преобразуем функцию, используя свойства логарифмов:

Вычисляем производную, используя правило дифференцирования суммы функций, формулу (11.8) и обобщенную таблицу производных:

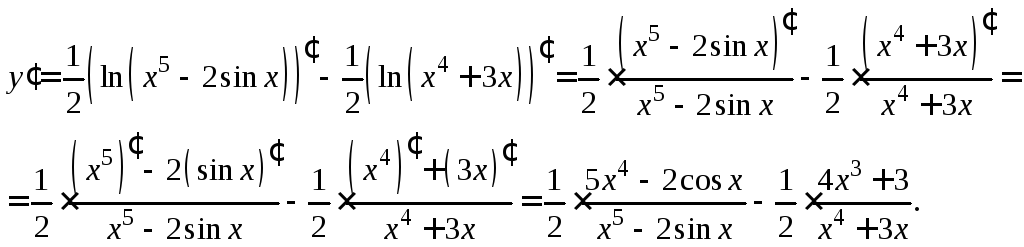
3) Рассмотрим функцию как где– также сложная функция. Применив формулу (11.8) дифференцирования сложной функции, обобщенную таблицу производных, а также правило дифференцирования частного двух функций, получим:

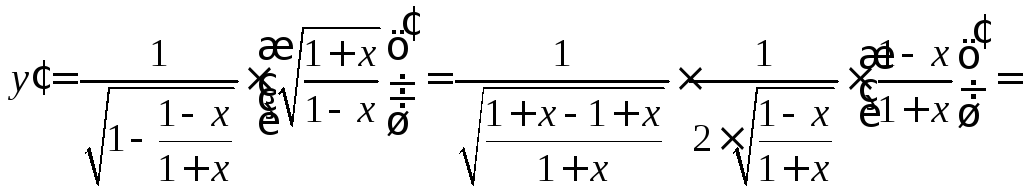
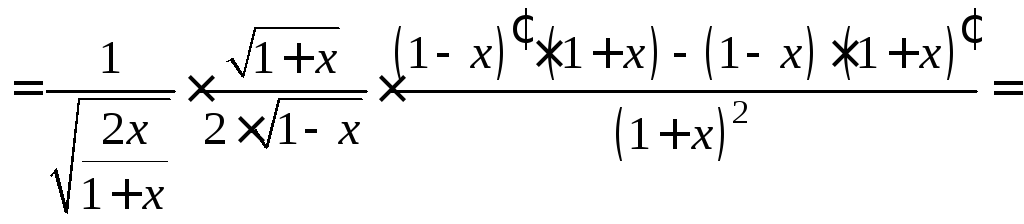
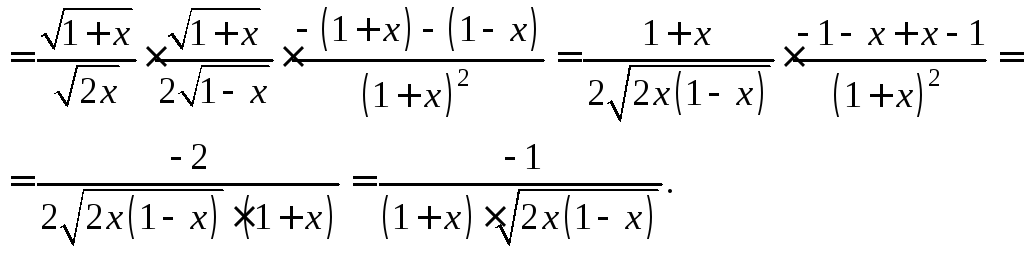
4) Пусть тогдаСогласно формуле (11.8), получим:

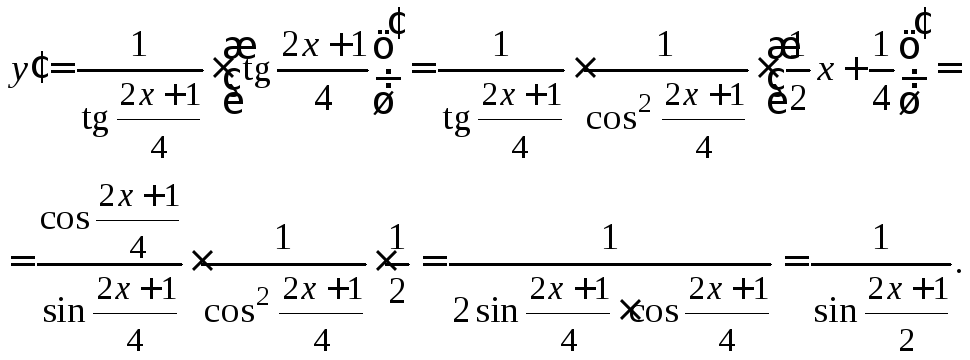
5) Рассмотрим функцию как где

Функцию можно представить в видегдеТогда:

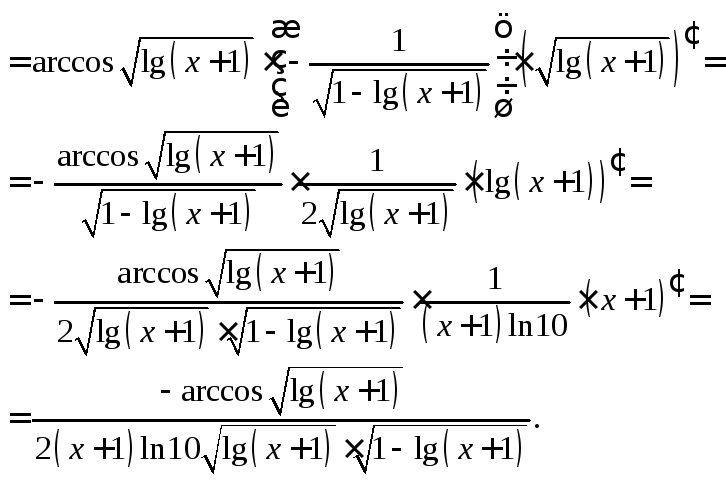
6) Перед тем как дифференцировать функцию, преобразуем выражение, пользуясь свойствами логарифма:

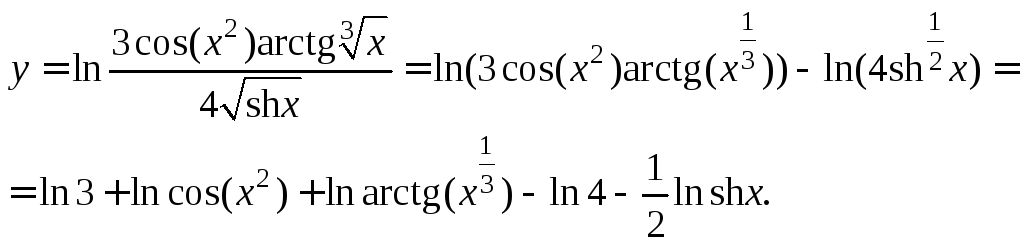
Продифференцируем полученное выражение по формулам (11.3)–(11.5), (11.8) и соответствующим формулам таблицы производных:

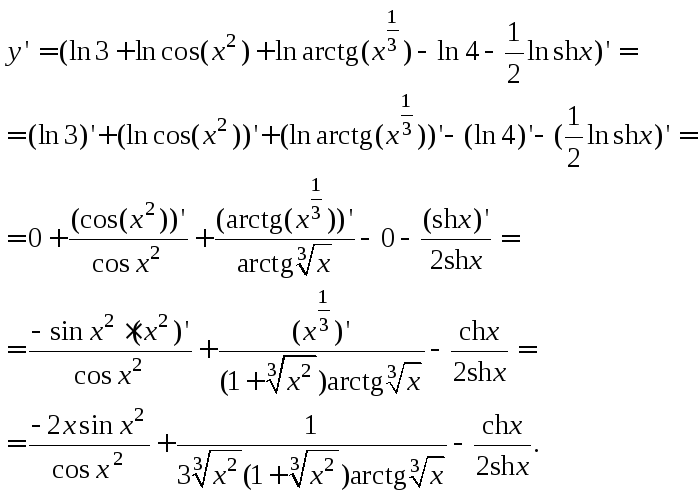
Применив далее формулы тригонометрии, окончательно получим:

Пример 2. Вычислить если

Решение. Это сложная функция с промежуточным аргументом Дифференцируем ее по формуле (11.8). При этом пользуемся первой формулой обобщенной таблицы производных при условии

Вычислим значение производной при

Пример 3. Вычислить если

Решение. Преобразуем функцию, используя свойства логарифмов:

Теперь продифференцируем выражение по формулам (11.3), (11.5), (11.8) и соответствующим формулам таблицы производных. Функцию рассмотрим какгде

Теперь вычислим

и

Тогда

Задания

I уровень

1.1. Найдите производную функции:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15) 16)

17) 18)

19) 20)

1.2. Найдите производную функции при данном значении аргумента:

1) 2)

3) 4)

5) 6)

7) 8)

1.3. Решите неравенство если и

II уровень

2.1. Вычислите если

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

2.2. Вычислите производную функции при заданном значении аргумента:

1)

2)

3)

4)

5)

6)

7)

8)

2.3. Вычислите значение производной предварительно упростив выражение:

1) 2)

3) 4)

2.4. Вычислите производную функции, предварительно упростив выражение:

1) 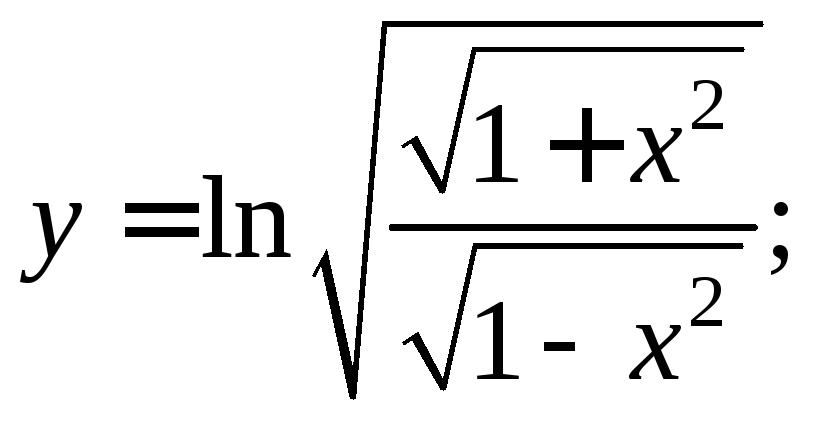2)

3) 4)

2.5. Известно, что иНайдите значение выражениягде

2.6. Найдите производную функции если

2.7. Найдите производную функции если

2.8. Докажите тождество:

1) если

б) если

Ш уровень

3.1. Найдите производную функции:

1) 2)

3) 4)

3.2. Найдите производную функции, предварительно преобразовав выражение по тригонометрическим формулам:

1) 2)

3) 4)

5)

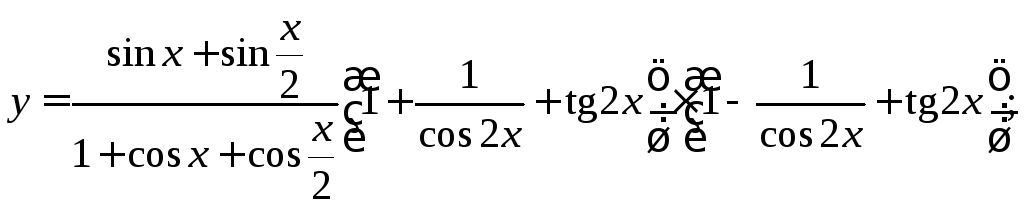
6)

3.3. Дана функция Определите, чему равно значение выражения

3.4. Даны функции иНайдите количество значенийx на отрезке для которых выполняется равенство