

РАЗДЕЛ 7. ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ
7.1. Динамические цепочки
7.1.1. Структура динамической цепочки
Динамические цепочки являются аналогами строк текущей длины.
В строке каждый следующий элемент занимает ячейку памяти со следующим по порядку адресом.
Элементы строки можно размещать в памяти произвольно, если каждый элемент снабдить явным указанием места, где находится следующий за ним элемент. В этом случае каждый элемент строки должен состоять из двух полей: в одном поле (Element) – символ сроки, в другом (Adrcled) – ссылка на следующий элемент строки (адрес следующего элемента).
Каждая такая пара называется звеном. Ссылки сцепляют звенья в одну
цепочку.
Такой способ представления упорядоченной последовательности элементов называется сцеплением. Сцепление применяется для представления любых сложных динамических структур данных – строк, списков, деревьев и так далее. В этом случае звено всегда состоит из двух частей – тела звена (элемента последовательности) и справочной части (ссылки на другие элементы структуры).
Таким образом, для представления звена необходимо использовать запись, состоящую из двух полей.
Пример 7.1.
Объявление звена цепочки.
Type
Adr = ^Zveno;
Zveno = Record
Element: Char;
Adrcled: Adr
End;
124
Впримере 7.1 тип Adr представляет собой ссылки на программные элементы типа Zveno.
Вданном примере имя типа Zveno используется до его описания при описании типа Adr (ссылочного типа). Ссылочный тип – единственный тип, где можно использовать имя до его описания. Обратную последовательность объявлений (вначале описать тип Zveno, а потом – тип Adr) в примере 7.1 использовать было бы нельзя (так как в типе Zveno используется неописанный тип Adr, а Zveno не является ссылочным типом).
Последнее звено цепочки должно быть снабжено ссылкой Nil (это признак конца цепочки).
Для работы с цепочкой необходимо использовать два указателя: ссылку на ее первое звено (Adr1) и ссылку на текущее звено (Adrzv). Ссылки должны иметь тип Adr. Например,
Var Adr1, Adrzv: Adr;
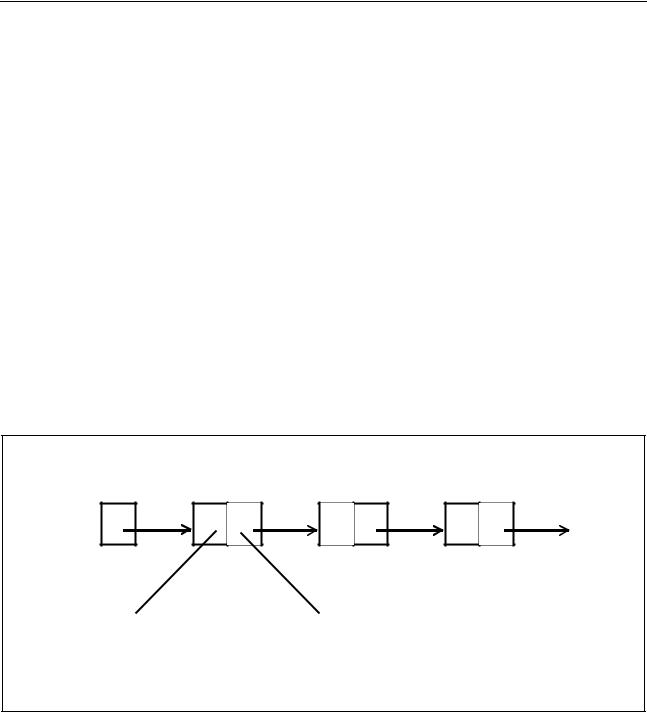
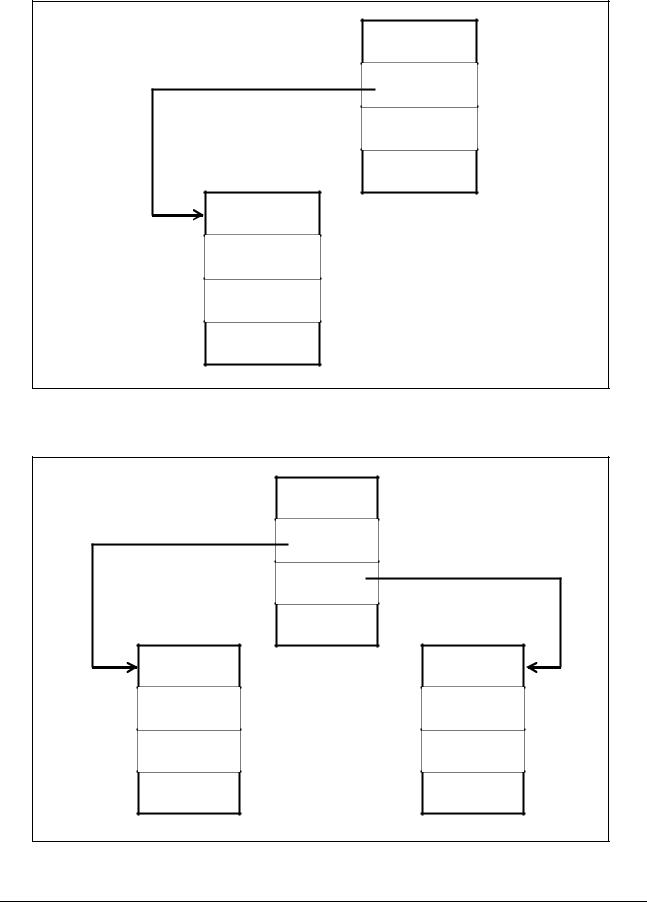
Схематично цепочка может быть представлена так, как изображает рисунок 7.1.
|
|
Первое звено |
|
|
|
Adr1 |
* |
* |
* |
* |
… |
Очередной |
Адрес |
элемент Element |
следующего |
|
элемента Adrcled |
Рисунок 7.1 – Схематическое представление цепочки
Для удобства работы с цепочкой в нее обычно включается заглавное «нулевое» звено (хотя это и не обязательно). В поле Adrcled данного звена содержится ссылка на первое звено цепочки (его адрес). Поле Element может быть использовано для хранения какой-либо информации о строке.
125

7.1.2. Формирование цепочки
Пусть имеется объявление звена цепочки, соответствующее примеру 7.1.
Алгоритм формирования цепочки:
1)Отвести область памяти для очередного звена. Его адрес занести в поле Adrcled текущего звена.
2)Новое звено сделать текущим (занести его адрес в указатель текущего звена Adrzv).
3)В поле Element текущего звена занести очередной символ.
4)В поле Adrcled текущего звена занести Nil.
5)Прочитать следующий символ исходного текста.
6)Повторить этапы алгоритма, начиная с первого этапа.
Предварительно перед выполнением этапов 1 – 6 алгоритма необходимо сформировать заглавное звено.
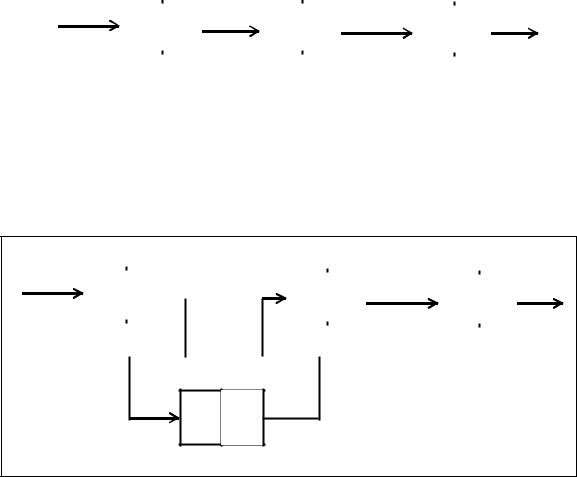
Схематические пояснения к алгоритму формирования цепочки с заглавным звеном представляет рисунок 7.2.
На данном рисунке номерами в фигурных скобках представлены действия соответствующих этапов алгоритма.
Adr1 |
Загл. зв. |
{1} |
|
{1} |
|
{1} |
|
* |
* |
1 |
* |
2 |
* |
3 |
* |
|
Nil |
|
Nil |
|
Nil |
|
Nil |
|
|
{3} |
{4} |
{3} |
{4} |
{3} |
{4} |
|
|
{2} |
|
{2} |
|
{2} |
|
|
|
|
|
|
|
|
|
Adrzv |
|
|
|
|
|
|
|
|
Рисунок 7.2 - Схематические пояснения |
|
|
||||
|
к алгоритму формирования цепочки |
|
|
||||
126

Пример 7.2.
Формирование цепочки. Ввод исходной строки и представление ее в виде цепочки. Признак окончания строки – точка. Раздел типов соответствует примеру 7.1.
…
Var
Adr1, Adrzv: Adr; |
{Adr1 – адрес заглавного звена, |
Simv: Char; |
Adrzv – адрес текущего звена} |
|
|
Begin |
|
{Формирование заглавного звена цепочки}
New (Adr1); |
{Отводится место в памяти для |
|
Adrzv := Adr1; |
заглавного звена цепочки} |
|
{Формируется адрес текущего звена} |
||
Adrzv^.Adrcled := Nil; |
{При формировании цепочки текущее |
|
|
|
звено всегда является последним, |
Read (Simv); |
поэтому адрес следующего звена – Nil} |
|
{Читается первая буква исходного текста} |
||
{Формирование текущих звеньев цепочки} |
||
While Simv <> ’.’ Do |
|
|
|
Begin |
|
{1} |
New (Adrzv^.Adrcled); |
|
{2} |
Adrzv := Adrzv^.Adrcled; |
|
{3} |
Adrzv^.Element := Simv; |
|
{4} |
Adrzv^.Adrcled := Nil; |
|
{5} |
Read (Simv); |
|
|
End |
|
…
Номера {1} – {5} операторов программы, приведенной в данном примере, соответствуют номерам этапов алгоритма формирования цепочки.
Над динамическими цепочками определены три операции:
•поиск;
•вставка;
•удаление.
127

7.1.3. Поиск элемента в цепочке
При поиске элемента необходимо последовательно перебирать все звенья цепочки. Для перехода от одного звена к следующему нужно в цикле выполнять оператор присваивания
Adrzv:= Adrzv^.Adrcled,
то есть присваивать указателю текущего звена в качестве нового значения ссылку на следующее звено.
Данный оператор присваивания является аналогом оператора
I := I+1,
выполняемого для получения номера I следующего элемента при векторном представлении строки типа Array Of Char или String.
Пример 7.3.
Поиск элемента в строке-цепочке (в продолжение примеров 7.1, 7.2). Подсчет числа его вхождений в строку.
…
Var
K: Integer;
Bykva: Char; Begin
…
Adrzv := Adr1; |
{Адресу текущего звена присваивается |
|
значение адреса нулевого звена |
K := 0; |
(заглавного)} |
{Счетчик числа вхождений искомого |
|
Read (Bykva); |
элемента} |
{Чтение буквы, которую нужно найти} |
|
While Adrzv^.Adrcled <> Nil Do |
{Пока не конец строки} |
Begin |
|
Adrzv := Adrzv^.Adrcled; |
{Указателю присваивается значение |
If Adrzv^.Element = Bykva |
адреса следующего звена} |
{Сравнивается содержимое поля элемента |
|
Then K := K+1; |
текущего звена с заданной буквой} |
|
|
End; |
|
128

…
7.1.4. Удаление элемента из цепочки
Исключаемый элемент наиболее удобно задавать при помощи ссылки на то звено, за которым следует этот элемент. При этом учитывается, что если какое-либо звено существует, но на него нет ссылки из другого звена, то оно недоступно при последовательном переборе звеньев цепочки. Поэтому это звено в цепочку не входит.
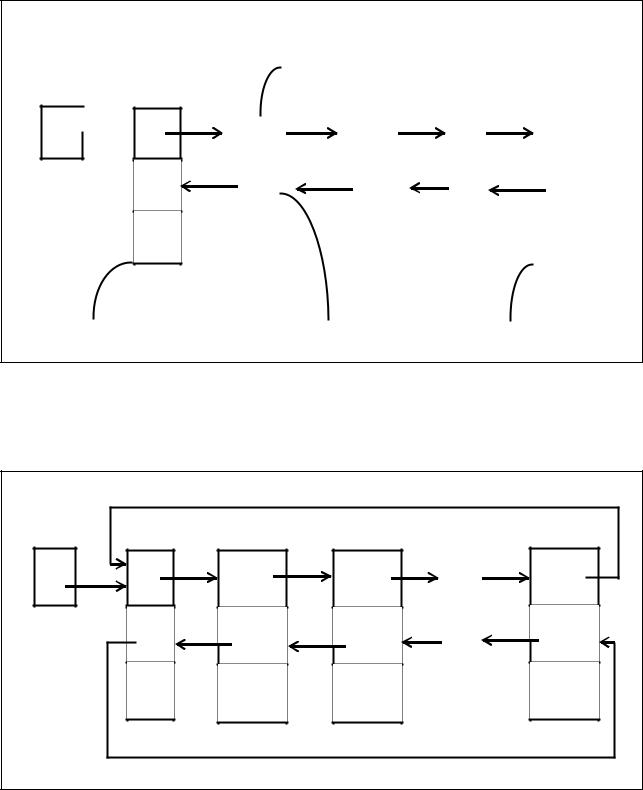
Например, в исходной цепочке (рисунок 7.3) необходимо удалить элемент 2. Для этого нужно, чтобы звено 1 ссылалось на звено 3 (рисунок 7.4).
1 |
* |
|
2 |
* |
|
3 |
* |
(фрагмент |
|
|
|
|
|
|
|
|
цепочки) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.3 – Фрагмент исходной цепочки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
* |
|
|
|
2 |
* |
|
|
|
3 |
* |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.4 – Результат удаления элемента 2
Таким образом, для исключения элемента из цепочки необходимо изменить ссылку у предшествующего ему элемента. В качестве новой ссылки у этого элемента следует принять ссылку, содержащуюся в исключаемом элементе.
129

Пример 7.4.
Удаление из цепочки второго элемента (в продолжение примеров 7.1 – 7.3, см. рисунок 7.3, рисунок 7.4).
Для удаления необходимо использовать оператор
Adrzv^.Adrcled:=Adrzv^.Adrcled^.Adrcled
Поле адреса |
Поле адреса элемента 2 |
элемента 1 |
.....................................................................................................( исключаемого ) |
........................................................................................... |
В этом случае в указателе текущего звена Adrzv должен находиться адрес элемента 1 (предшествующего исключаемому).
Пример 7.5.
Процедура удаления элемента из цепочки (в продолжение примеров 7.1 –
7.3).
Procedure Udal (Zv: Adr); |
|
Var A: Adr; |
{A – вспомогательная переменная} |
Begin |
|
A := Zv^.Adrcled; |
{В А заносится адрес удаляемого |
Zv^.Adrcled := Zv^.Adrcled^.Adrcled; |
звена} |
{Удаление звена из цепочки} |
|
{или равноценно Zv^.Adrcled := А^.Adrcled;} |
|
Dispose (A) |
{Освобождение памяти, занимаемой |
End; |
удаленным звеном} |
|
|
Вданном примере в качестве параметра Zv процедуры должен передаваться адрес звена, предшествующего удаляемому.
Впримере 7.4 удаление элемента из цепочки выполняется быстрее, но память расходуется неэффективно (так как отсутствует процедура Dispose).
Впримере 7.5 удаление звена из цепочки прооисходит медленнее, но память расходуется эффективнее.
Тот или иной вариант удаления необходимо выбирать, исходя из конкретных требований к характеристикам программы.
130
7.1.5. Вставка элемента в цепочку
Вставка элемента в цепочку основывается на объединении отдельных звеньев в единую цепочку.
Пусть в исходную цепочку (рисунок 7.5) после элемента 1 необходимо вставить элемент 4.
|
|
|
|
|
|
|
|
|
|
|
1 |
* |
|
2 |
* |
|
3 |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.5 – Фрагмент исходной цепочки
После вставки цепочка схематически будет выглядеть так, как изображает рисунок 7.6.
1 |
* |
|
|
2 |
* |
|
|
|
|
|
3 |
* |
|||||
|
|
|
|
|
|
|
|
|
4) |
|
|
|
3) |
|
|
4 *
Рисунок 7.6 – Результат вставки элемента 4
Алгоритм вставки нового звена после заданного:
1)Создать новую динамическую переменную (запись типа Zveno), которой будет представленно вставляемое звено.
2)В поле Element этой пременной занести вставляемый элемент (символ).
3)В поле Adrcled этой переменной занести ссылку, взятую из поля Adrcled предшествующего звена.
4)В поле Adrcled предшествующего звена занести ссылку на это вставляемое звено.
131

Номерами 3), 4) (см. рисунок 7.6) обозначены действия, соответствующие третьему и четвертому этапам алгоритма.
Пример 7.6.
Процедура вставки элемента в цепочку.
Procedure Vstav (Zv: Adr; El: Char); |
{Zv – адрес звена, предшествующего |
|
Var |
вставляемому} |
|
|
||
|
Q: Adr; |
|
Begin |
|
|
{1} |
New (Q); |
|
{2} |
Q^.Element := El; |
|
{3} |
Q^.Adrcled := Zv^.Adrcled; |
|
{4} |
Zv^.Adrcled := Q |
|
End;
Номера операторов в данном примере соответствуют номерам этапов алгоритма вставки.
7.1.6. Линейный однонаправленный список
Динамическая строка-цепочка является частным случаем линейного однонаправленного списка. В случае строки информационными элементами списка являются символы (тип Char). В общем случае информационными элементами списка могут быть значения любого типа – числа, массивы, записи и т.п. Принцип организации информационных элементов в список – тот же: информационный элемент очередного звена снабжается ссылкой на следующее звено.
Пример 7.7.
Определение структуры звена однонаправленного списка.
Type Adres1 = ^Zveno1;
Zveno1 = Record
Adrcled: Adres1;
Element: <Тип_элемента_списка>
End;
132

Элементами списка являются значения одного и того же типа. Недостаток однонаправленного списка – по нему можно двигаться
только в одном направлении, от заглавного звена к последнему звену списка. Это замедляет работу с ним.
7.2. Двунаправленные списки
Двунаправленные списки, в отличие от однонаправленных, позволяют от каждого звена двигаться по списку в любом направлении.
Каждое звено двунаправленного списка содержит два поля ссылочного типа. Значением одного поля является ссылка на последующее звено списка. Значением другого поля является ссылка на предыдущее звено списка.
Структура звена двунаправленного списка определяется описанием типа, приведенным в примере 7.8.
Пример 7.8.
Описание типа звена двунаправленного списка.
Type
Adr2 = ^Zveno2;
Zveno2 = Record
Adrcled: Adr2;
Adrpred: Adr2;
Element: <Тип элемента-списка>
End;
Схематично двунаправленный список с заглавным звеном изображает рисунок 7.7.
На данном рисунке «элем. i» (элемент i) представляет собой информационную часть i-ого звена.
У заглавного звена списка нет предыдущего элемента. У последнего звена списка нет последующего элемента. Поэтому в поле Adrcled последнего звена и в поле Adrpred заглавного звена двунаправленного списка должна быть пустая ссылка Nil.
На основе двунаправленного списка могут быть организованы
двунаправленные кольцевые списки.
В кольцевом списке значением поля Adrcled последнего звена является ссылка на заглавное звено, значением поля Adrpred заглавного звена является
133
ссылка на последнее звено (рисунок 7.8).
Ссылка на следующее звено
Указатель
списка
*  *
*
Nil |
|
* |
|
* |
… |
Nil |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
* |
|
* |
… |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
элем.K |
|
элем.1 |
|
элем.2 |
|
|
|
|
|
|
|
|
Заглавное звено |
Ссылка на предыдущее звено |
Последнее звено |
Рисунок 7.7 – Представление двунаправленного списка с заглавным звеном
Указатель |
|
|
|
|
|
списка |
|
|
|
|
|
* |
* |
* |
* |
… |
* |
|
|
|
|
|
|
|
* |
* |
* |
… |
* |
|
|
|
|
|
|
|
|
элем.1 |
элем.2 |
|
элем.K |
Рисунок 7.8 – Представление двунаправленного кольцевого списка с заглавным звеном
(первый способ организации кольца)
134

Данный рисунок отражает первый способ организации кольцевого списка. При этом способе заглавное звено списка включается в кольцо.
При втором способе способ организации кольцевого списка заглавное звено списка в кольцо не включается (рисунок 7.9).
* |
* |
* |
* |
|
Nil |
* |
* |
|
|
элем.1 |
элем.2 |
…
…
*
*
элем.K
Рисунок 7.9 – Представление двунаправленного кольцевого списка с заглавным звеном
(второй способ организации кольца)
Достоинство первого способа организации кольцевого списка – просто реализуется вставка нового звена как в начало списка, так и в конец.
Недостаток – при циклической обработке элементов списка необходимо проверять, не является ли очередное звено заглавным звеном списка.
У второго способа организации кольцевого списка данный недостаток отсутствует, но труднее реализовывается добавление звена в конец списка.
Над двунаправленными списками определены те же три операции, что и над строкой-цепочкой:
•поиск элемента в списке;
•вставка элемента в указанное место списка;
•удаление из списка заданного элемента.
Для работы сдвунаправленными списками необходимо использовать два указателя – на заглавное звено и на текущее звено.
Ниже рассмотрена их реализация для первого способа организации кольцевого списка.
135

7.2.1. Вставка элемента
Пусть в программе имеется описание типа, приведенное в примере 7.8.
Алгоритм вставки элемента в указанное место двунаправленного кольцевого списка:
1)Порождение нового звена.
2)Занесение вставляемого элемента в информационное поле порожденного звена.
3)Занесение в поле Adrcled порожденного звена ссылки на следующий элемент из звена, предшествующего вставляемому.
4)Занесение в поле Adrpred порожденного звена ссылки на предыдущий элемент из звена, следующего за вставляемым.
5)Занесение в поле Adrpred следующего за вставляемым звена ссылки на вставляемое звено.
6)Занесение в поле Adrcled предшествующего звена ссылки на вставляемое звено.
Действия, необходимые для вставки элемента в двунаправленный кольцевой список с заглавным звеном, схематически поясняют рисунок 7.10 – рисунок 7.11.
Фрагмент исходного списка иллюстрирует рисунок 7.10.
|
|
|
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.10 - Фрагмент исходного двунаправленного списка
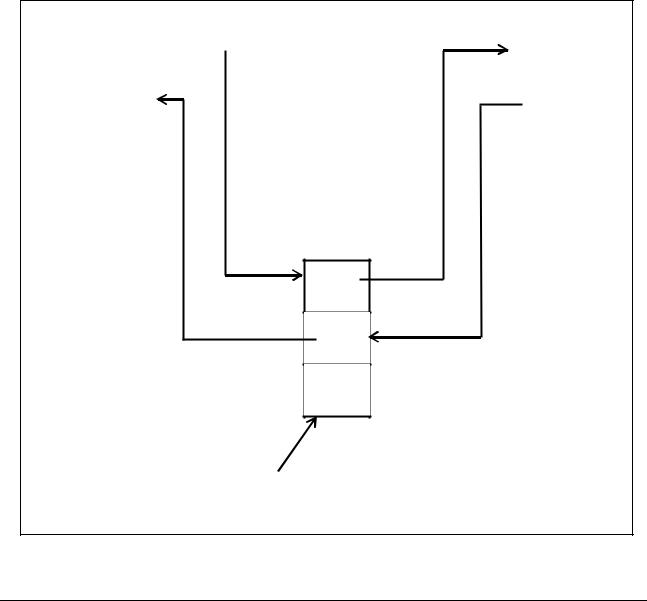
Пусть в исходный список после элемента 1 вставляется элемент 3. Соответствующий фрагмент результирующего списка будет иметь вид, который изображает рисунок 7.11.
На данном рисунке номера 1) – 6) соответствуют номерам этапов алгоритма вставки.
136
* |
|
|
|
|
* |
|
|
|
|
|
|
* |
|
6) |
3) |
* |
|
|
|
|
|||
1 |
|
|
|
|
2 |
|
|
|
|
|
|
4) |
5) |
*
*
3
2)
Q |
* |
|
|
1) |
|
|
|||
|
|
|
|
|
Рисунок 7.11 - Фрагмент результирующего двунаправленного списка
Пример 7.9.
Процедура вставки.
Procedure Vstav (Elem: <Тип_элемента_списка>; Predzv: Adr2);
{Elem – вставляемый элемент, Predzv – ссылка на предшествующий элемент}
Var Q: Adr2; Begin
{1} New (Q);
{2} Q^.Element := Elem;
{3} Q^.Adrcled := Predzv^.Adrcled; {4} Q^.Adrpred := Predzv;
137

{5} |
Predzv^.Adrcled^.Adrpred := Q; |
{6} |
Predzv^.Adrcled := Q; |
End;
В данном примере номера операторов, приведенные в комментариях, соответствуют номерам этапов алгоритма вставки. Реализация этапа 4 в примере отличается от этапа 4 алгоритма вставки, поскольку ссылка на предшествующее звено в процедуру Vstav передается в качестве параметра.
7.2.2.Создание двунаправленного кольцевого списка с заглавным звеном
Пусть в программе имеется описание типа, приведенное в примере 7.8. Для создания кольцевого списка можно использовать процедуру вставки,
приведенную в примере 7.9. При этом на каждом шаге создания список должен быть закольцован.
Пример 7.10.
Ввод исходного текста и представление его в виде двунаправленного кольцевого списка с заглавным звеном. Признак окончания текста – точка. Раздел типов соответствует примеру 7.8.
Var |
|
|
|
|
Ring: Adr2; |
{Адрес заглавного звена кольца} |
|
|
Bykva: Char; |
{Символ исходного текста} |
|
Begin |
|
|
|
{7} |
New (Ring); |
{Отведено место в памяти для заглавного звена} |
|
{8} |
Ring^.Adrcled := Ring; |
{Закольцовывается заглавное звено, так как} |
|
{9} |
Ring^.Adrpred := Ring; |
{на каждом промежуточном этапе список |
|
|
Read (Bykva); |
должен быть кольцом} |
|
|
{Чтение первой буквы текста} |
||
|
While Bykva <> ’.’ Do |
|
|
|
Begin |
|
|
|
Vstav (Bykva, Ring^.Adrpred); |
{Вызов процедуры вставки. Адрес |
|
|
|
предыдущего созданного звена (последнего |
|
|
|
звена кольца) всегда хранится в заглавном звене |
|
|
Read (Bykva) |
в поле Adrpred} |
|
|
{Чтение очередной буквы текста} |
||
138
|
End |
|
|
|
|
|
|
|
|
End. |
|
|
|
|
|
|
|
|
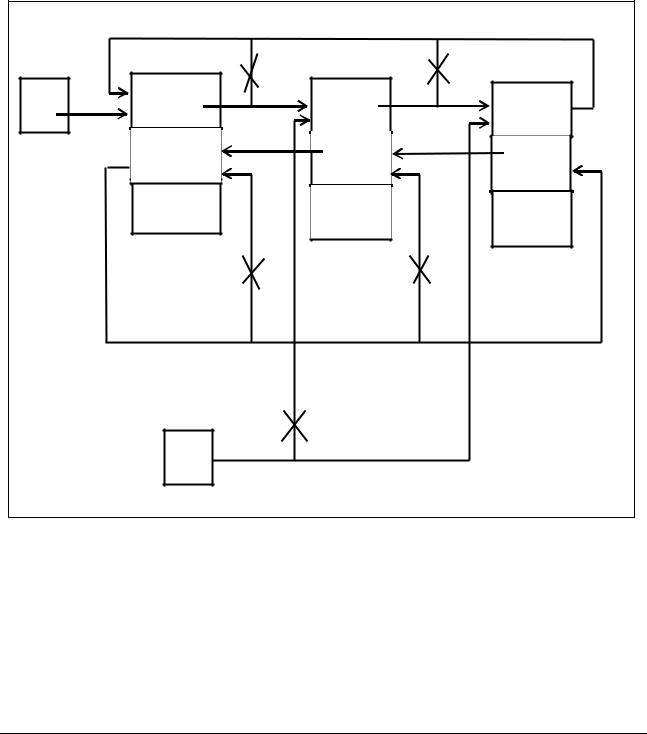
Схематические пояснения к данной программе содержит рисунок 7.12. |
|||||||
Ring |
|
8) |
|
|
3) |
|
3) |
|
* |
Adrcled |
6) |
* |
|
6) |
* |
|
|
|
7) |
|
4) |
|
4) |
|
|
|
|
Adrpred |
* |
|
* |
|
|||
|
|
|
|
|||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Заглавное |
9) |
2) |
5) |
|
2) |
5) |
|
|
|
звено |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
1) |
|
|
|
Q |
* |
|
|
|
|
|
|
|
|
Рисунок 7.12 – Схематические пояснения |
|
|
||||
|
|
|
к программе примера 7.10 |
|
|
|
||
На данном рисунке цифрами 1) – 6) обозначены номера этапов алгоритма вставки, приведенного в предыдущем подразделе, цифрами 7) – 9) – номера соответствующих операторов из примера 10.
Напомним, что список закольцовывается после добавления каждого нового звена.
7.2.3. Удаление элемента
Пусть в программе имеется описание типа, приведенное в примере 7.8.
139
Алгоритм удаления элемента:
1)Занесение в поле Adrpred следующего за удаляемым звена ссылки на предшествующее удаляемому звено из поля Adrpred удаляемого звена;
2)Занесение в поле Adrcled предшествующего удаляемому звена ссылки на следующее за удаляемым звено из поля Adrcled удаляемого звена;
3)Уничтожение удаляемого звена.
На двух следующих рисунках приведены схематические пояснения к удалению элемента из двунаправленного списка.
Пусть в изображенном фрагменте исходного списка удаляется звено 2 (рисунок 7.13).
* |
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|
* |
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
Ydzv *
Рисунок 7.13 – Фрагмент исходного двунаправленного списка
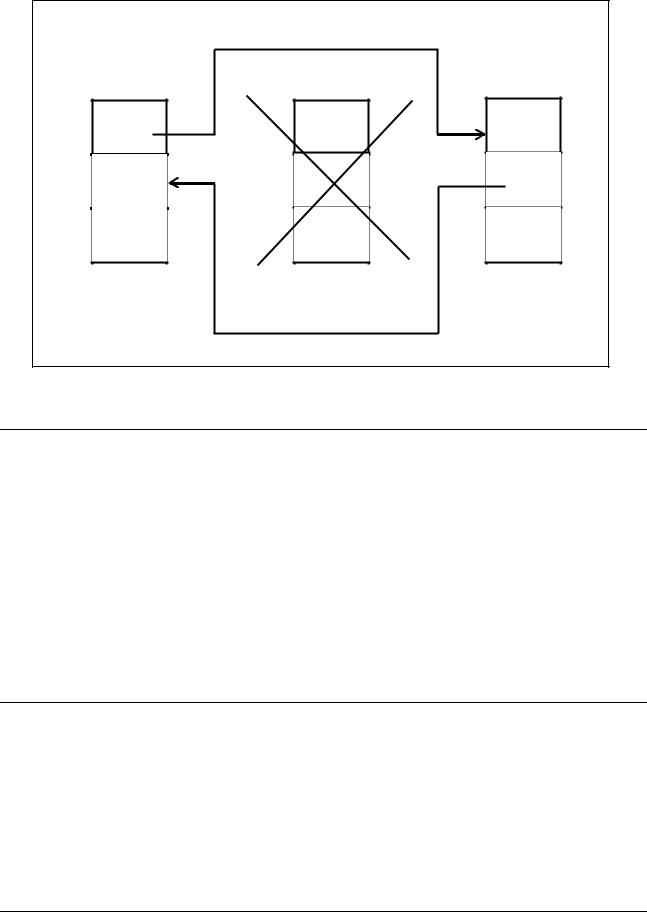
Результат удаления звена 2 выглядит так, как иллюстрирует рисунок 7.14. Номера связей на данном рисунке соответствуют номерам этапов
алгоритма удаления.
140
|
2) |
|
* |
* |
* |
|
3) |
|
* |
* |
* |
1 |
2 |
3 |
|
1) |
|
|
Рисунок 7.14 - Результат удаления звена 2 |
|
Пример 7.11.
Процедура удаления звена из двунаправленного списка. Номера операторов соответствуют номерам этапов алгоритма удаления звена.
Procedure Udalen (Udzv: Adr2); {Udzv – ссылка на удаляемое звено} Begin
{1} Udzv^.Adrcled^.Adrpred := Udzv^.Adrpred; {2} Udzv^.Adrpred^.Adrcled := Udzv^.Adrcled; {3} Dispose (Udzv);
End;
7.2.4. Поиск элемента
Поиск элемента в двунаправленном кольцевом списке аналогичен поиску элемента в цепочке (см. п. 7.1.3).
Особенность поиска заключается в том, что в кольцевом списке формально нет последнего элемента, так как каждый элемент имеет ссылку на следующий. Это нужно учитывать при организации цикла поиска.
141

Пример 7.12.
Логическая функция поиска элемента в двунаправленном кольцевом списке с заглавным звеном. Если искомый элемент в списке есть, возвращаемое значение функции равно True, а параметру Iskadr присваивается ссылка на звено, содержащее данный элемент.
Function Poisk (Adr: Adr2; Elem: <Тип_элемента_списка>; Var Iskadr: Adr2):
Boolean; {Adr – ссылка на заглавное звено; Elem – искомый элемент;
Iskadr – адрес искомого элемента}
Var |
|
P, Q: Adr2; |
{В Р будет храниться адрес заглавного |
B: Boolean; |
звена, в Q – адрес текущего звена} |
|
|
Begin |
|
B := False; |
{B – логическая переменная (факт |
P := Adr; |
наличия искомого элемента)} |
{В P занесен адрес заглавного звена} |
|
Iskadr := Nil; |
|
Q:=P^.Adrcled; |
{В Q занесен адрес первого звена} |
While (P<>Q) And Not B Do |
{Поиск, пока не дошли до заглавного |
Begin |
звена и не нашли искомый элемент} |
|
|
If Q^.Element = Elem Then |
{Найден искомый элемент} |
Begin |
|
B := True; |
|
Iskadr := Q |
{Адрес искомого элемента} |
End; |
|
Q := Q^.Adrcled |
{Переход к следующему звену} |
End; |
|
Poisk := B |
{Возвращаемое значение} |
End; |
|
7.3. Очереди и стеки
В программировании имеется структура данных, называемая очередью. Понятие очереди в программировании аналогично понятию реальной очереди из повседневной жизни.
Очередь является динамической структурой. Длина очереди и набор образующих ее элементов изменяется с течением времени.
142
Над очередью определены две операции:
•занесение элемента в очередь (заказа на обслуживание);
•выбор элемента из очереди (для его обслуживания); выбранный элемент из очереди исключается.
Вочереди доступны две позиции: ее начало (из этой позиции выбирается элемент из очереди) и конец (в эту позицию помещается заносимый в очередь элемент).
Различают два основные вида очередей, отличающиеся по дисциплине (способу) обслуживания находящихся в них элементов.
Впервом виде очередей заказ, поступивший в очередь первым, выбирается первым для обслуживания и удаляется из очереди. Это дисциплину обслуживания очереди называют FIFO (First In – First Out – первый в очередь
–первый из очереди).
Во втором виде очередей заказ, поступивший в очередь последним, выбирается первым для обслуживания и удаляется из очереди. Эту дисциплину обслуживания называют LIFO (Last In – First Out – последний в очередь – первый из очереди).
Очередь второго вида называется стеком.
7.3.1. Очередь LIFO
Наиболее часто в программировании используются очереди второго вида
–стеки. Принцип их работы – «Последний пришел – первый вышел».
Встеке доступна единственная позиция, называемая вершиной стека – это позиция, в которой находится последний по времени поступления в стек элемент.
Наиболее быстрое выполнение операций над стеком обеспечивает его представление в виде динамической цепочки звеньев (однонаправленного списка). Вершиной стека обычно является первое звено цепочки. Заглавное звено в цепочке стека не нужно, так как в стеке доступна только его вершина.
При использовании структуры однонаправленного списка стек задается с помощью описания типа, приведенного в примере 7.7, и дополнительно может быть введен тип указателя, представляющего стек как единую структуру, то есть ссылка на вершину стека Stek:
Type
<Задание стека по примеру 7.7>;
Stek = Adres1;
Реальный стек вводится с помощью описания переменной:
143
Var
St: Stek;
Схематично стек изображается аналогично цепочке (рисунок 7.15).
St |
|
|
* |
|
|
* |
|
… |
|
Nil |
* |
|
|
|
|
|
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
элемент |
|
|
|
элемент |
|
|
элемент |
|
|
|
|
Ссылка на |
|
|
|
|
|
|
|
|
|
|
вершину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
стека |
Вершина |
|
|
|
|
|
Дно стека |
|||
|
|
|
|
|
|
|
||||
|
|
стека |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Рисунок 7.15 – Схематичное представление стека
К началу использования стека его нужно сделать пустым:
St := Nil;
А. Занесение элемента в стек
Пусть в программе имеется описание типа, приведенное в примере 7.7.
Алгоритм занесения элемента в стек:
1)Создание нового звена.
2)Занесение в новое звено элемента.
3)Занесение в новое звено адреса предыдущей вершины стека.
4)Созданное звено сделать вершиной стека.
Пример 7.13.
Процедура занесения элемента в стек. Первый параметр задает нужный стек (если их несколько), второй – заносимое в него значение.
Procedure Zanes (Var St: Stek; El:<Тип_элемента_стека>); Var
Q: Adres1; Begin
{1} New (Q);
144

{2} Q^.Element := El; {3} Q^.Adrcled := St; {4} St := Q
End;
Номера операторов в данной программе соответствуют номерам этапов алгоритма занесения элемента в стек.
Б. Выбор элемента из стека
Пусть в программе имеется описание типа, приведенное в примере 7.7.
Алгоритм выбора элемента из стека:
1)Прочитать значение из вершины стека.
2)Запомнить ссылку на старую вершину.
3)Исключить первое звено из стека.
4)Уничтожить первое звено.
Пример 7.14.
Процедура выбора элемента из стека. Первый параметр задает нужный стек (если их несколько), во второй передается значение из вершины стека.
Procedure Vibor (Var St: Stek; Var A: <Тип_элементов_стека>); Var
Q: Adres1; Begin
{1} A := St^.Element; {2} Q := St;
{3} St := St^.Adrcled; {4} Dispose (Q)
End;
Номера операторов в данной программе соответствуют номерам этапов алгоритма выбора элемента из стека.
Если необходимо ускорить процедуру выбора, то операторы Q := St и Dispose(Q) можно не применять. Однако это приведет к неэффективному использованию памяти.
145

В. Создание стека
Пусть в программе имеется описание типа, приведенное в примере 7.7. Для создания стека может быть использована процедура Zanes из примера
7.13.
Пример 7.15.
Создание стека. Ввод исходного текста в стек. Признак окончания текста
– точка.
…
Var
St: Adres1;
Bykva: Char; Begin
St := Nil; Read (Bykva);
While Bykva <>’.’ Do Begin
Zanes (St, Bykva); Read (Bykva)
End
End.
7.3.2. Очередь FIFO
Принцип работы – “Первый пришел, первый вышел”.
Для организации такой очереди используются две ссылочные переменные типа Adres1 (см. пример 7.7): Left – для указания начала и Right – для указания конца очереди.
Добавление элемента в очередь осуществляется в соответствии со значением Right. Затем значение Right изменяется и указывает на последний занесенный элемент.
Выборка элементов из очереди происходит, исходя из значения Left. Затем Left изменяется и указывает на следующий элемент очереди.
Если в очереди один элемент, значение Right равно значению Left. Такое равенство может использоваться как признак окончания очереди при последовательном выборе элементов из нее.
146

А. Занесение элемента в очередь
Пусть в программе имеется описание типа, приведенное в примере 7.7.
Алгоритм занесения элемента в очередь:
1)Cоздание нового звена.
2)Занесение в последнее звено адреса нового звена.
3)Занесение Nil в поле Adrcled нового звена.
4)Занесение элемента в информационное поле нового звена.
5)Созданное звено сделать концом очереди.
Пример 7.16.
Процедура занесения элемента в очередь. Первый параметр – Right – адрес последнего занесенного элемента, второй – заносимое в очередь значение.
Procedure Dobavl (Var Right: Adres1; El: <Тип_элементов_очереди>);
Var |
|
|
|
Q: Adres1; |
|
Begin |
|
|
{5} |
New (Q); |
{1-й этап алгоритма занесения} |
{6} |
Right^.Adrcled := Q; |
{2-й этап алгоритма занесения} |
{7} |
Q^.Adrcled := Nil; |
{3-й этап алгоритма занесения} |
{8} |
Q^.Element := El; |
{4-й этап алгоритма занесения} |
{9} |
Right:=Q |
{5-й этап алгоритма занесения} |
End;
Б. Выбор элемента из очереди
Пусть в программе имеется описание типа, приведенное в примере 7.7.
Алгоритм выбора элемента из очереди:
1)Чтение значения из начала очереди.
2)Запоминание ссылки на начало очереди.
3)Исключение первого звена из начала очереди.
4)Уничтожение первого звена.
147

Пример 7.17.
Процедура выбора элемента передачи адреса начала очереди. начала очереди.
из очереди. Параметр Left используется для В параметр Elem передается значение из
Procedure Udal (Var Left: Adres1; Var Elem: <Тип_элементов_очереди>);
Var |
|
|
|
Q: Adres1; |
|
Begin |
|
|
|
Elem := Left^.Element; |
{1-й этап алгоритма выбора} |
{10} |
Q := Left; |
{2-й этап алгоритма выбора} |
{11} |
Left := Left^.Adrcled; |
{3-й этап алгоритма выбора} |
|
Dispose(Q) |
{4-й этап алгоритма выбора} |
End;
В. Организация очереди
Пусть в программе имеется описание типа, приведенное в примере 7.7. Организация очереди основана на использовании операции занесения
элемента в очередь
Пример 7.18.
Организация очереди. Ввод исходного текста в очередь. Признак окончания текста – точка. Используется процедура Dobavl занесения элемента в очередь (см. пример 7.16).
...
Var
Right, Left: Adres1; Bykva: Char;
Begin
Read (Bykva); {1} New (Left);
{2} Left^.Adrcled := Nil; {3} Left^.Element := Bykva; {4} Right := Left;
Read (Bykva);
While Bykva <>’.’ Do Begin
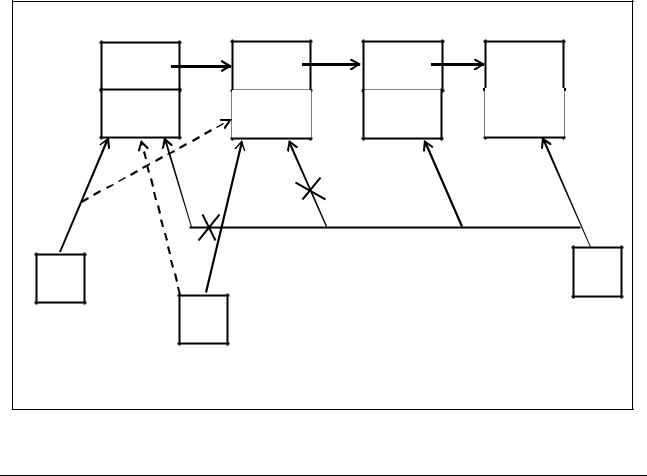
Dobavl (Right, Bykva);
Порождение первого звена очереди (левого).
148
|
Read (Bykva) |
|
|
|
|
|
|
|
|
End. |
End |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.16 содержит схематические пояснения к примерам 7.16 – 7.18. |
|||||||||
Номерами на данном рисунке обозначены действия над очередью FIFO, |
|||||||||
соответствующие номерам операторов в данных примерах. |
|
||||||||
|
{2} |
|
{6} |
{7} |
|
{6} |
{7} |
{6} |
{7} |
|
|
Nil |
|
Nil |
|||||
|
Nil |
* |
|
* |
|
* |
Nil |
||
|
|
|
|
|
|
|
|||
|
Bykva |
|
|
|
|
|
|
|
|
|
{3} |
|
|
{8} |
|
|
{8} |
|
{8} |
|
{1} |
|
{4} |
|
|
{9} |
|
{9} |
|
|
{11} |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
{10} |
{5} |
|
|
|
|
* |
||
* |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Left |
|
Q |
* |
|
|
|
|
|
Right |
|
|
|
|
|
|
|
|||
|
Рисунок 7.16 – Схематические пояснения к примерам 7.16 – 7.18 |
||||||||
7.4. Таблицы
7.4.1. Общие сведения
В настоящее время широко используются автоматизиованные информационные системы (АИС). Их назначение: хранение большого числа сведений, прием новых сведений и выдача хранимых сведений по запросам. Обычно сведения предоставляются записями.
Основная задача при создании АИС – организация выдачи по запросу любой из записей, независимо от того, какая запись выдавалась перед ней.
149
Для организации АИС используются структуры данных, называемые таблицами. В таблице каждой записи соответствует свое имя. Таким образом, таблица – это набор именованных записей. Имя записи называется ключом записи.
Для организации эффективного поиска записи необходимо, чтобы над ключами можно было реализовать операции сравнения (=, <, >), поэтому желательно, чтобы ключи были упорядоченными.
В качестве ключей наиболее удобно использовать целые положительные числа или строки символов одинаковой длины.
Над таблицей определены следующие операции:
•поиск в таблице записи с заданным ключом;
•включение в таблицу записи с заданным ключом (если в таблице уже есть запись с таким ключом, то старая запись заменяется на новую);
•исключение из таблицы записи с заданным ключом.
7.4.2. Способы организации таблиц
Возможны следующие способы организации таблиц.
1) Однонаправленный список.
Таблица представляется с помощью однонаправленного списка. Каждое звено списка должно содержать ключ записи, текст записи, ссылку на следующее звено.
Достоинства способа:
а) эффективное использование памяти машины (дополнительная информация в звене – только ссылка на следующее звено);
б) простой алгоритм перебора записей для поиска нужной записи; в) простота включения в таблицу заведомо новой записи – как новое
звено в конец списка.
Недостаток способа – большое время поиска нужной записи за счет следующих факторов:
а) при наличии в таблице N записей для поиска нужной необходимо просмотреть в среднем N/2 элементов списка;
б) если в таблице нет записи с нужным ключом, то нужно просмотреть все N записей.
2) Однонаправленный список с упорядоченными записями.
Записи в списке следуют по возрастанию их ключей.
Достоинства способа: меньшее время поиска записи по сравнению со способом 1). Поиск записи требует в среднем просмотра N/2 записей, независимо от того, есть эта запись в таблице или нет.
150

Недостаток: усложняется процедура включения новой записи в таблицу.
3) Однонаправленный список с отдельным хранением текста записи.
Используется для ускорения поиска записи. Тексты записей хранятся отдельно от ключей. При ключе хранится только ссылка на текст записи.
Схематическое представление таблицы в виде списка с отдельным хранением текста записи имеет вид, который представляет рисунок 7.17.
Tab |
* |
|
|
* |
|
|
* |
… |
Nil |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ключ1 |
|
|
Ключ2 |
|
|
КлючN |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
* |
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запись1 |
|
Запись2 |
|
ЗаписьN |
|
|
|
|
|
Рисунок 7.17 - Схематическое представление таблицы
ввиде списка с отдельным хранением текста записи
4)Представление в виде массива.
Каждый элемент таблицы является записью, содержащей два поля – ключ записи и ссылку на текст записи. Такие элементы обьединяются не в список, а в одномерный массив.
Пример 7.19.
Объявление типа таблицы при использовании массива записей, содержащих два поля – ключ записи и ссылку на текст записи.
Type
151
Index = 1..N; |
|
Text = <Тип_текста_записи>; |
|
Adr = ^Text; |
|
Element = Record |
|
Kl: Integer; |
{Ключ} |
Adrzap: Adr |
|
End; |
|
Mas = Array [Index] Of Element; |
|
Var |
|
Tabl: Mas; |
|
Схематическое представление таблицы в виде массива иллюстрирует рисунок 7.18.
Tabl |
|
|
|
|
|
|
…… |
|
|
||
Ключ1 |
|
|
Ключ2 |
КлючN |
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
* |
|
|
|
* |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Запись1 |
|
Запись2 |
|
ЗаписьN |
|
|
|
|
|
Рисунок 7.18 - Схематическое представление таблицы в виде массива
Для организации эффективного поиска в таблице, реализованной описываемым способом, необходимо, чтобы элементы массива были упорядочены по возрастанию ключей.
Задача поиска записи с заданным ключом сводится к задаче нахождения элемента массива Tabl, в котором содержится этот ключ. Если определен индекс I этого элемента, то искомая запись является значением переменной
Tabl[I].Adrzap^.
Для поиска элемента с заданным ключом используется метод половинного деления (дихотомический поиск). Его сущность заключается в следующем.
152

Берется средний элемент массива с индексом (номером) N/2. Если искомый ключ К меньше чем ключ в элементе с номером N/2, то требуемый элемент находится в первой половине массива, в противном случае – во второй. На следующем этапе нужная половина массива опять делится пополам и определяется, в какой из половин находится соответствующий элемент и так далее. Процесс завершается, если на очередном шаге серединный компонент текущей зоны поиска содержит заданный ключ (требуемая запись найдена) или если зона поиска оказалась пустой (записи с нужным ключом в таблице нет).
Так как на каждом шаге зона поиска уменьшается в два раза, то для завершения поиска требуется не более
1 + log2 N
шагов. Таким образом, эффект способа по сравнению со способами 1 и 2 быстро возрастает с ростом N.
Пример 7.20.
Логическая функция Poisk поиска нужного ключа в таблице, реализующая метод дихотомического поиска. Функция Poisk возвращает значение True, если нужный ключ в таблице есть, и False в противном случае. Функция Poisk имеет два параметра: К – искомый ключ, Nomer – номер элемента массива Tabl, в котором хранится нужный ключ К (в параметрпеременную Nomer функция устанавливает значение индекса (номера элемента) массива Tabl, содержащего нужный ключ).
Пусть имеется объявление по примеру 7.19.
Function Poisk (K: Integer; Var Nomer: Index): Boolean;
Var |
|
Lev, Prav: Integer; |
{Левая и правая границы зоны поиска} |
B: Boolean; |
|
I: I ndex; |
|
Begin |
|
Lev := 1; |
|
Prav := N; |
{N – размер таблицы Tabl} |
B := False; |
|
Nomer := 0; |
{Если в Nomer остается значение ноль, |
Repeat |
значит, искомого ключа в Tabl нет} |
|
|
I := (Lev + Prav) Div 2; |
|
If K = Tabl[I].Kl Then |
|
Begin |
|
153

B := True;
Nomer := I End
Else
If K < Tabl[I].Kl Then Prav := I - 1
Else
Lev := I+1
Until B Or (Lev > Prav); {Искомый ключ найден или пустая зона (нет нужного ключа)}
Poisk := B {Возвращаемое значение функции}
End;
Недостаток способа 4 – он плохо приспособлен для реализации включения и исключения записей, так как необходимо сдвигать все последующие после вставляемого или исключаемого элементы массива в ту или другую сторону для поддержания упорядоченности элементов. Поэтому способ 4 удобно использовать, если таблица изменяется редко.
5) Двоичное дерево.
Реализация таблицы в виде двоичного дерева позволяет эффективно выполнять все три операции над таблицей. Работа с двоичными деревьями описана в следующем подразделе.
7.5. Двоичные деревья
7.5.1. Структура двоичного дерева
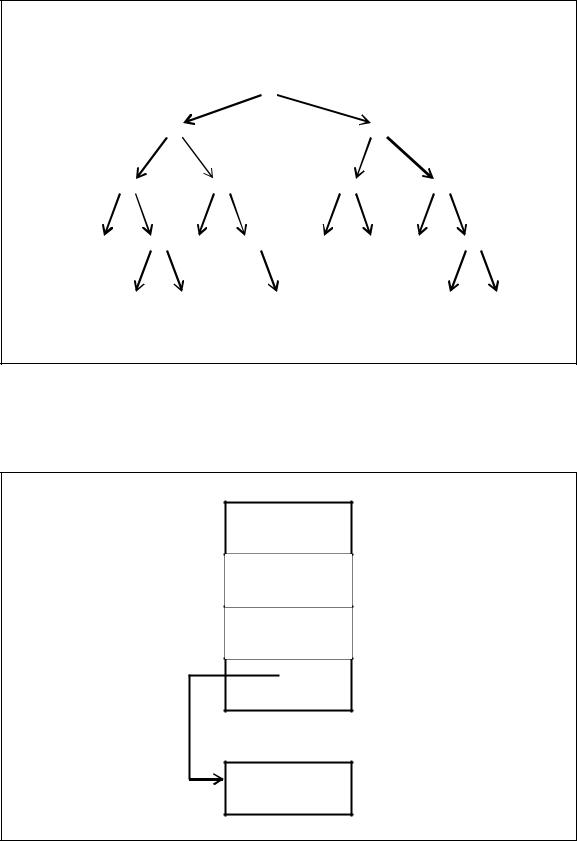
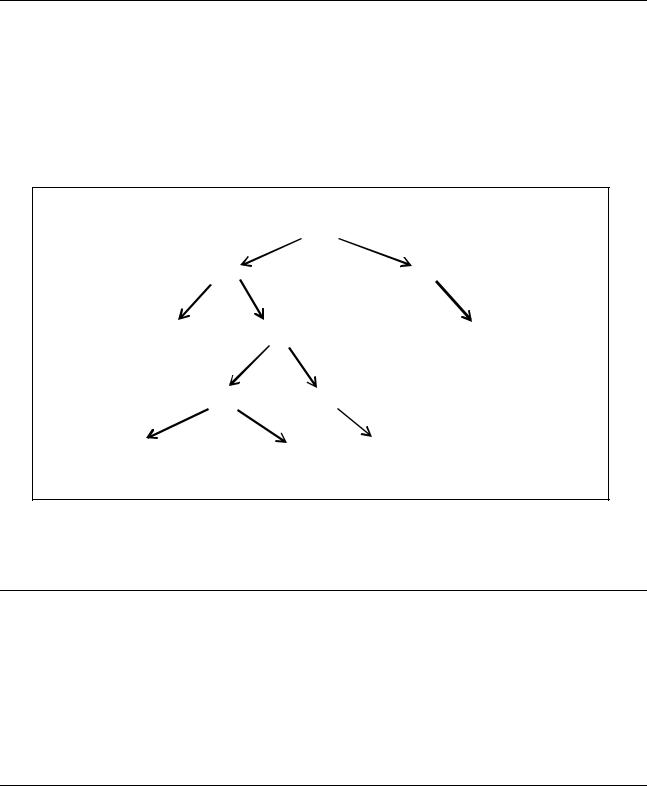
Схематично двоичное дерево можно представить как набор вершин, соединенных стрелками (ветвями, рисунок 7.19).
Из каждой вершины выходит не более двух ветвей, направленных влевовниз или вправо-вниз. В каждую вершину, помимо одной, входит одна стрелка. Вершина, в которую не входит ни одна стрелка, называется корнем дерева. Вершины, из которых не выходит ни одна стрелка, называются листьями.
При представлении таблицы в виде дерева тексты записей хранятся отдельно. Каждая вершина дерева (звено) является записью, состоящей из четырех полей: ключа записи (Kl), ссылки на вершину влево-вниз (Lev), ссылки
на вершину вправо-вниз (Prav) и ссылки на текст записи (*). Данную структуру звена представляет рисунок 7.20.
154
Корень
дерева
|
|
* |
|
|
|
|
* |
|
|
* |
|
* |
|
* |
* |
* |
|
* |
* * |
* |
* |
* * |
* |
* |
* |
* |
|
* |
* |
Листья дерева |
|
|
|
||
Рисунок 7.19 – Схематическое представление двоичного дерева
Kl
Lev
Prav
*
Запись
Рисунок 7.20 – Структура звена двоичного дерева
155

7.5.2. Построение дерева
Принцип построения дерева заключается в следующем.
Первая запись делается корнем дерева. Если ключ следующей записи меньше ключа корня, то этой записи ставится в соответствие левая вершина, в противном случае – правая. Ключ К каждой последующей записи сравнивается последовательно с ключом корня, а затем с ключами тех записей, которые находятся на соответствующей ветви дерева. В зависимости от сравнения ключа К с ключом в очередной вершине осуществляется переход влево или вправо от нее до тех пор, пока не будет найдена подходящая вершина, к которой можно присоединить новую вершину с ключом К. В зависимости от результата сравнения ключа в этой вершине с поступившим ключом К вновь сформированная вершина становится левой или правой для найденной вершины.
Пример 7.21.
Построение дерева. В первоначально пустую таблицу заносятся последовательно поступающие записи с ключами 100, 20, 120, 50, 15, 130, 55, 30, 35, 60, 33, 28.
Построенное в соответствии с вышеприведенным принципом построения дерево имеет вид, который представляет рисунок 7.21.
С учетом структуры каждого звена дерева последовательность построения дерева по данному примеру выглядит следующим образом.
После поступления первой записи с ключом К1 = 100 дерево имеет вид, который иллюстрирует рисунок 7.22.
Так как у этой вершины пока нет вершин справа-внизу и слева-внизу, то в соответствующие поля (ссылки на левые и правые вершины) необходимо установить пустую ссылку (Nil).
После поступления второй записи с ключом К2 = 20 дерево имеет вид, который представляет рисунок 7.23.
Так как К2 < К1, то вновь созданная вершина дерева становится левой по отношению к первой. Для этого в поле Lev (адрес левой вершины) вершины 1 заносится адрес созданной вершины 2.
После поступления третьей записи с ключом К3 = 120 дерево приобретает вид, который изображает рисунок 7.24.
Так как К3 > К1, то вновь созданная вершина дерева становится правой по отношению к первой вершине, то есть в поле Prav вершины 1 заносится адрес вершины 3.
Аналогичные действия производятся для подключения всех
156
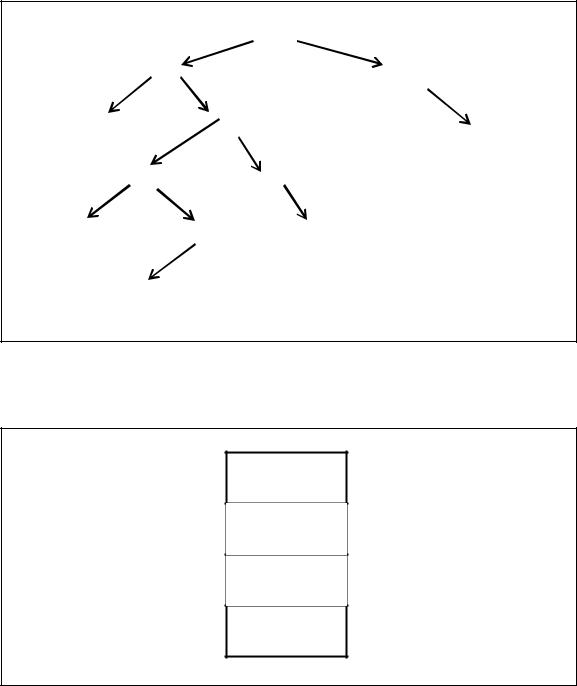
последующих вершин дерева.
|
|
100 |
20 |
|
120 |
15 |
50 |
130 |
|
|
|
30 |
|
55 |
28 |
35 |
60 |
33 |
|
|
Рисунок 7.21 – Результирующее дерево
K1=100
Nil
Nil
*
Рисунок 7.22 – Вид дерева после поступления первой записи
157
|
100 |
|
Lev |
|
Nil |
|
* |
|
K2=20 |
|
Nil |
|
Nil |
|
* |
Рисунок 7.23 – Вид дерева после поступления второй записи |
|
|
100 |
|
Lev |
|
Prav |
|
* |
20 |
К3=120 |
Nil |
Nil |
Nil |
Nil |
* |
* |
Рисунок 7.24 - – Вид дерева после поступления третьей записи |
|
158

Таким образом, подходящей вершиной, к которой можно подсоединить новую вершину, является вершина соответствующей ветви дерева, у которой поле Lev или Prav (в зависимости от соотношения ключей ее и новой вершины) равно Nil.
Двоичное дерево может быть введено в употребление с помощью описания, приведенного в примере 7.22.
Пример 7.22.
Описание двоичного дерева.
Type
Tekst = <Тип_значения_записи>;
Adrt = ^Tekst;
Adrzv = ^Zveno;
Zveno = Record
Kl:I nteger;
Lev, Prav: Adrzv;
Adr: Adrt
End;
Var
Dvder: Adrzv;
Над двоичными деревьями определены те же операции, что и над таблицами в целом:
•поиск записи с заданным ключом;
•включение записи с заданным ключом (если уже есть запись с таким ключом, то старая запись заменяется на новую);
•исключение записи с заданным ключом.
7.5.3. Поиск записи в дереве
Рассмотрим реализацию поиска записи в двоичном дереве на примере. Пусть имеется объявление по примеру 7.22.
Пример 7.23.
Логическая функция, отыскивающая вершину дерева с заданным ключом. Формальные параметры: К - заданный ключ, D - ссылка на корень дерева, в
159

котором ведется поиск, Rez- переменная, которой присваивается ссылка на найденное звено в случае успешного поиска (такая вершина есть), или ссылка на вершину, после обработки которой поиск прекращен, в случае неуспешного поиска (закончилась ветвь).
Function Poisk (K: Integer; Var D, Rez: Adrzv): Boolean;
Var |
|
P, Q: Adrzv; |
|
B: Boolean; |
{В – признак того, что ключ найден} |
Begin |
|
B := False; |
|
P := D; |
{В Р заносится адрес корня дерева, затем |
|
в Р будет храниться адрес вершины, |
Q := Nil; |
подлежащей обработке} |
|
|
If D <> Nil Then |
{Анализ, не является ли дерево пустым} |
Repeat |
|
Q := P; |
{В Q будет храниться адрес |
If P^.Kl = K Then |
обработанной вершины} |
|
|
B := True |
{Найдена нужная вершина} |
Else |
|
If K < P^.Kl Then |
|
P := P^.Lev |
|
Else |
|
P := P^.Prav |
|
Until B Or (P = Nil); |
{Поиск, пока не найден ключ (В=True) |
|
или пока не закончилась |
Poisk := B; |
соответствующая ветвь} |
{Возвращаемое значение} |
|
Rez := Q; |
{В Q – адрес звена с нужным ключом |
End; |
или адрес конца ветви} |
|
Скорость поиска в двоичном дереве примерно равна скорости дихотомического поиска (см. пример 7.20).
7.5.4. Включение записи в дерево
Для включения записи в дерево нужно найти в нем вершину, к которой можно присоединить новую вершину, соответствующую включаемой записи. Алгоритм поиска нужной вершины аналогичен алгоритму поиска вершины с
160

заданным ключом (см. пример 7.23). Нужная вершина найдена, если в качестве очередной ссылки, определяющей ветвь продолжения поиска, окажется ссылка
Nil.
Таким образом, для поиска вершины, к которой можно присоединить включаемую запись, можно воспользоваться алгоритмом поиска вершины с заданным ключом, реализованным в примере 7.23. Такая вершина найдена, если В = False. В этом случае в Rez находится адрес вершины, к которой можно подсоединить включаемую вершину.
Для простоты будем считать, что в таблице нет записи с тем же ключом, что и у включаемой записи.
Пусть имеется объявление по примеру 7.22.
Пример 7.24.
Процедура включения записи в дерево. Параметры процедуры: К - ключ, D - адрес корня дерева, Zap - текст вставляемой записи.
Procedure Vkl (K: Integer; Var D: Adrzv; Zap: Tekst);
Var |
|
Q, S: Adrzv; |
|
T: Adrt; |
|
Begin |
|
If Not Poisk (K, D, Q) |
Then |
Begin |
|
New (T); |
{Создано звено для занесения текста записи} |
T^ := Zap; |
{Занесен в таблицу текст записи} |
New (S); |
{Сформирована новая вершина в дереве} |
S^.Kl := K; |
{Занесен ключ в поле Kl новой вершины} |
S^.Adr := T; |
{Занесен адрес текста записи в поле Adr новой |
S^.Lev := Nil; |
вершины} |
|
|
S^.Prav := Nil; |
{Созданная вершина сделана “листом” дерева} |
If D = Nil Then |
|
D := S |
{Если дерево еще пусто (создается), то |
Else |
созданное звено делается корнем дерева} |
|
|
If K < Q^.Kl |
{В Q-адрес вершины, к которой |
|
присоединяется новая вершина} |
Then
Q^.Lev := S
Else
Q^.Prav := S
End
161
End;
7.5.5. Удаление записи из дерева
Если соответствующая вершина является конечной (“лист” дерева) или из нее выходит только одна ветвь, то для удаления записи достаточно скорректировать соответствующую ссылку у вершины-предшественника
(рисунок 7.25).
*
*
а) |
б) |
Рисунок 7.25 – Удаление записи из дерева: а) из удаляемой записи выходит одна ветвь; б) удаляемая запись является «листом» дерева
В этих случаях в соответствующее поле Lev или Prav вершиныпредшественника нужно занести содержимое поля Lev или Prav удаляемой вершины (если удаляемая вершина является “листом”, то это будет ссылка Nil).
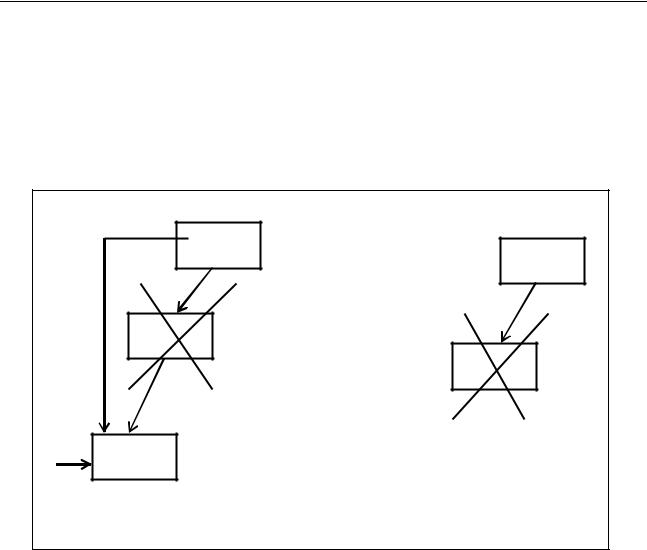
Если из удаляемой вершины выходит две ветви, то нужно найти подходящее звено дерева, которое можно было бы вставить на место удаляемого. Таким звеном является:
а) Самый правый элемент левого поддерева.
Данный элемент является самым большим в левом от удаляемой вершины поддереве.
162
Для достижения этого звена необходимо перейти в следующую от удаляемой вершину по левой ветви, а затем переходить в очередные вершины только по правой ветви до тех пор, пока очередная правая ссылка не будет равна Nil.
Пример 7.25.
Исключение из дерева, созданного в примере 7.21, звена с ключом 50 (см. рисунок 7.21), используя для замещения самый правый элемент левого поддерева. Результат исключения имеет вид, который представляет рисунок
7.26.
|
|
100 |
|
20 |
120 |
15 |
35 |
130 |
30 55
28 |
33 |
60 |
Рисунок 7.26 – Результат исключения звена с ключом 50 (вариант 1)
б) самый левый элемент правого поддерева.
Данный элемент является самым маленьким в правом от удаляемой вершины поддереве.
Для достижения этого звена необходимо перейти в следующую от удаляемой вершину по правой ветви, а затем переходить в очередные вершины только по левой ветви до тех пор, пока очередная левая ссылка не будет равна
Nil.
163

Пример 7.26.
Исключение из дерева, созданного в примере 7.21, звена с ключом 50 (см. рисунок 7.21), используя для замещения самый левый элемент правого поддерева. Результат исключения представляет рисунок 7.27.
|
|
100 |
20 |
|
120 |
15 |
55 |
130 |
|
|
|
30 |
|
60 |
28 |
35 |
|
33
Рисунок 7.27 – Результат исключения звена с ключом 50 (вариант 2)
Таким образом, при исключении из двоичного дерева вершины с заданным ключом необходимо учесть три случая удаления:
1)звена с заданным ключом в дереве нет;
2)звено с заданным ключом имеет не более одной ветви;
3)звено с заданным ключом имеет две ветви.
Пример 7.27.
Рекурсивная процедура Udder исключения вершины с заданным ключом из дерева. Процедура реализует вариант а) исключения в соответствии с примером 7.25. Параметры: K - искомый ключ, D - адрес корня дерева.
Пусть имеется объявление по примеру 7.22.
Procedure Udder (Var D: Adrzv; K: I nteger);
Var
Q: Adrzv;
164
{Рекурсивная процедура Ud, реализующая третий случай удаления}
Procedure Ud (Var R: Adrzv); |
{При первом вызове в качестве |
||
|
|
|
фактического параметра передается адрес |
|
Begin |
|
левой после удаляемой вершины} |
|
|
|
|
|
If R^.Prav=Nil |
Then |
{Анализируемая вершина является самой |
|
Begin |
|
правой в левом поддереве} |
|
|
|
|
{6} |
Q^.Kl := R^.Kl; |
{Занесение в поле КL удаляемого звена |
|
|
|
|
ключа из замещающего звена (в Q – |
|
Q^.Adr := R^.Adr; |
адрес удаляемого звена)} |
|
{7} |
{Занесение в поле Adr удаляемого звена |
||
|
|
|
ссылки на текст записи из замещающего |
|
Q := R; |
|
звена} |
{8} |
|
{Занесение в Q адреса замещающего |
|
|
R := Q^.Lev |
звена} |
|
{9} |
{Занесение в поле Prav звена- |
||
|
|
|
предшественника замещающему |
|
|
|
содержимого поля Lev из замещающего |
|
End |
|
звена} |
|
Else |
{Анализируемая вершина не является |
|
|
|
||
|
Ud (R^.Prav) |
самой правой в левом поддереве} |
|
{11} |
{Рекурсивный вызов процедуры Ud |
||
|
|
|
для перехода к следующей правой |
|
End; |
|
вершине левого поддерева} |
|
|
{Конец процедуры Ud} |
|
Begin |
|
{Тело процедуры Udder} |
|
|
If D = Nil Then |
|
{Первый случай удаления} |
|
Writeln (‘Звена с заданным ключом в дереве нет’) |
||
|
Else |
|
|
|
If K < D^.Kl |
Then |
{Ключ в анализируемой вершине больше |
|
Udder (D^.Lev, K) |
заданного} |
|
{2} |
{Рекурсивный вызов процедуры Udder |
||
|
|
Else |
для перехода к вершине слева-внизу} |
|
|
{Ключ в анализируемой вершине меньше |
|
|
If K > D^.Kl Then |
или равен заданному} |
|
|
{Ключ в анализируемой вершине меньше |
||
{3} |
Udder (D^.Prav, K) |
заданного} |
|
{Рекурсивный вызов процедуры Udder |
|||
|
|
Else |
для перехода к вершине справа-внизу} |
|
Begin |
{Звено с заданным ключом найдено} |
|
|
|
|
|
|
|
|
165 |
{1} |
Q := D; |
{Занесение в Q адреса удаляемого звена |
|
|
|
(он взят из поля Lev или Prav звена- |
|
|
|
предшественника)} |
|
|
If Q^.Prav = Nil Then |
{Второй случай удаления} |
|
{4} |
D := Q^.Lev |
{Занесение в поле Lev или Prav звена- |
|
|
|
предшественника удаляемому ссылки |
|
|
Else |
на звено, следующее за удаляемым} |
|
|
|
||
|
If Q^.Lev = Nil Then {Второй случай удаления} |
||
{5} |
D := Q^.Prav |
{Занесение в поле Lev или Prav звена- |
|
|
|
предшественника удаляемому ссылки |
|
|
|
на звено, следующее за удаляемым} |
|
{10} |
Else |
{Третий случай удаления} |
|
|
Ud (Q^.Lev) |
{Вызов процедуры Ud; переход в левое |
|
|
End |
для удаляемой вершины поддерево} |
|
End; |
{Конец процедуры Udder} |
||
|
|||
В |
данном примере параметр D оформлен как параметр-переменная |
||
процедуры Udder. При рекурсивном вызове процедуры Udder в качестве соответствующего D фактического параметра используется поле Lev (см. оператор {2}) или Prav (см. оператор {3}) того звена, от которого мы перешли к текущему звену (то есть звена-предшественника). Поэтому операторы {4} и {5} обеспечивают занесение в поле Lev или Prav звена-предшественника ссылки на звено, следующее за удаляемым, из удаляемого звена.
Аналогичные пояснения справедливы и для переменной R (R оформлена как параметр-переменная процедуры Ud).
Процедура Ud предназначена для поиска подходящей замещающей вершины, для занесения значений из полей замещающего звена в поля удаляемого звена и для удаления замещающего звена со своего предыдущего места.
Рисунок 7.28 содержит схематические пояснения к примеру 7.27 (в привязке к примерам 7.21 и 7.25). Удаляется звено с ключом 50. Замещающее звено – звено с ключом 35.
Номера в фигурных скобках соответствуют номерам операторов в примере 7.27.
Исходное значение D – адрес корня дерева. По оператору {2} осуществляется переход к вершине 20, по оператору {3} – к вершине 50, по оператору {10} – к вершине 30, по оператору {11} – к вершине 35.
166

|
|
|
|
|
|
* |
D |
|
|
|
|
100 |
|
|
|
|
|
|
D^.Lev |
* |
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
{2} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
120 |
|
|
|
|
|
|
Nil |
|
|
|
* |
|
|
|
|
|
|
|
D^.Lev^.Prav |
|
|
* |
||
|
|
* |
|
|
|||
|
|
|
|
|
|||
|
15 |
|
|
|
|
|
130 |
|
|
|
{3} |
|
|
|
|
|
|
|
|
|
|
|
|
Q=D^.Lev^.Prav |
{1} |
|
50 |
35 |
{6} |
|
|
Q |
* |
|
{10} |
* |
|
|
|
|
|
|
* |
|
|
|
|
|
|
Q^.Lev |
{7} |
|
|
|
|
|
|
|
|
55 |
|
||
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
* |
Q^.Lev^.Prav |
|
|
60 |
|
|
|
|
|
|
|
||
|
28 |
|
{11} |
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
{8} |
|
|
* |
|
|
|
|
|
|
{9} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
Рисунок 7.28 - Схематические пояснения к примеру 7.27 |
||||||
167

D^.Lev, D^.Lev^.Prav (см. рисунок 7.28) соответствуют значению фактического параметра, передаваемому на вход формального параметра D на текущем шаге выполнения программы; Q^.Lev, Q^.Lev^.Prav – значению фактического параметра, передаваемому на вход формального параметра R на текущем шаге выполнения программы.
Выделенные поля звеньев дерева (см. рисунок 7.28) представляют собой значения фактического параметра (D^.Lev^.Prav), соответствующего формальному параметру D для удаляемого звена, и фактического параметра (Q^.Lev^.Prav), соответствующего формальному параметру R для замещающего звена.
Для физического удаления удаляемого звена необходимо вместо оператора {4} в процедуре использовать составной оператор
Begin
D := Q^.Lev;
Dispose (Q)
End;
а вместо оператора {5} – оператор
Begin
D := Q^.Prav;
Dispose(Q)
End;
Для физического удаления замещающего звена после оператора {9} в процедуре нужно добавить оператор
Dispose (Q).
168
