01.Кинематика
.pdf
Путь, пройденный при равнопеременном движении
|
t |
|
S(t) |
| V0 |
at | dt |
0
Если движение прямолинейное вдоль оси X, то
S(t) x(t) x0 |
V0t |
at 2 |
V 2 |
V 2 |
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
2 |
|
|
2a |
V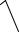 
V02 2aS
x x0 |
v0t |
at 2 |
|
2 |
|||
|
|
(16)
(17)
(18)
(20)
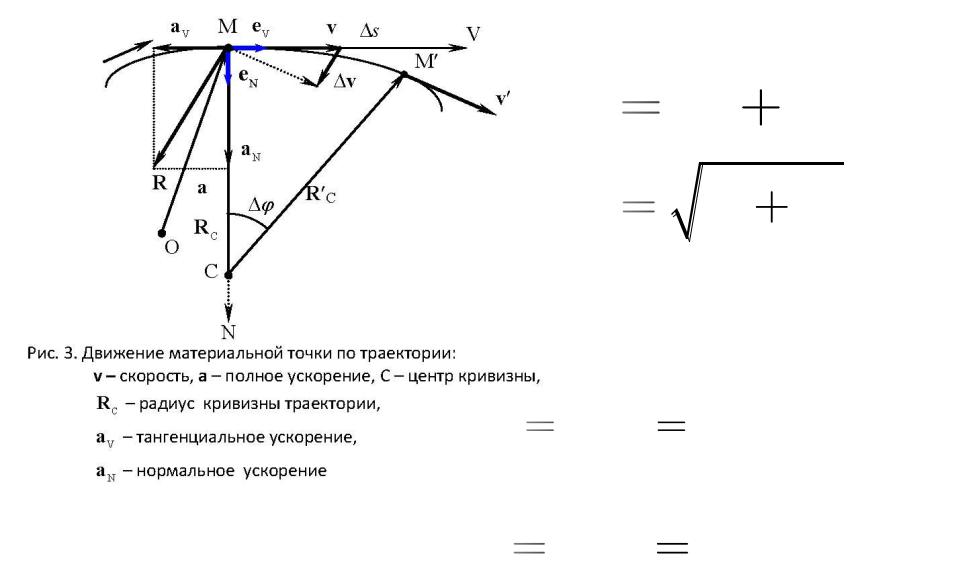
Криволинейное движение
|
|
Полное ускорение |
||||||||
|
|
a |
an |
|
a |
(21) |
||||
|
|
|
|
|
|
|
|
|
||
|
|
a |
a2 |
|
a2 |
(22) |
||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
Нормальное, или |
|
|
||||||
|
|
центростремительное |
||||||||
|
|
ускорение |
|
|
|
|
||||
|
an |
aneN |
V 2 |
eN |
(23) |
|||||
|
|
|
R |
|
||||||
|
|
|
|
|
|
|
|
|
||
Тангенциальное, или |
a |
a eV |
|
|
dV |
eV |
(24) |
|||
|
|
|
|
|
||||||
касательное ускорение: |
|
|
dt |
|
||||||
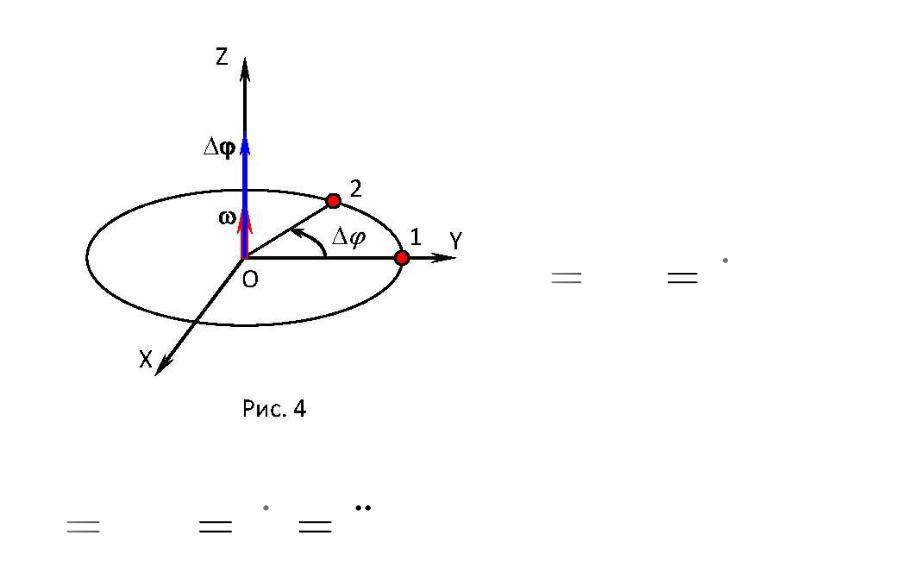
Движение материальной точки по окружности
φ – угловое перемещение
( псевдовектор, аксиальный вектор)
dφ
ω φ (25)
dt
– угловая скорость
(псевдовектор)
ε |
dω |
ω φ – угловое ускорение |
(26) |
|
dt |
||||
|
(псевдовектор) |
|
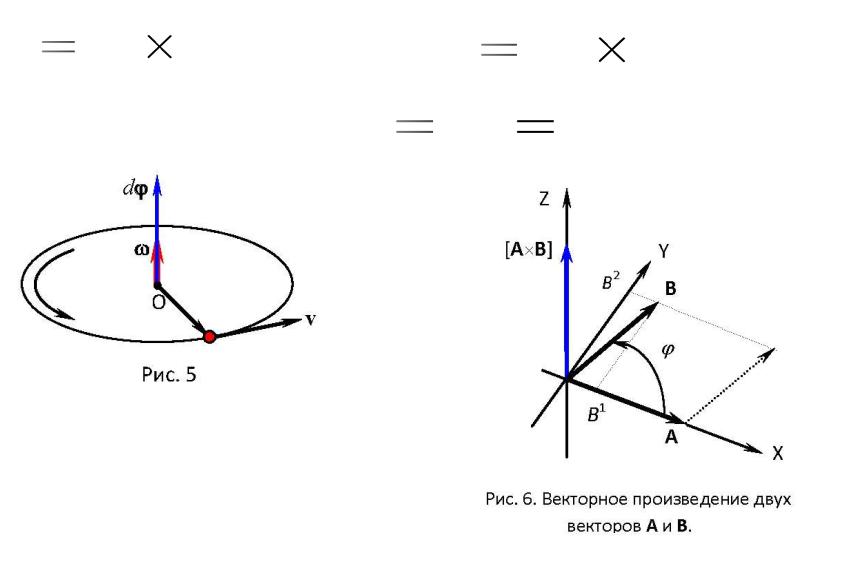
Связь угловой и линейной скорости
v [ω R] (27) |
C |
[A B] |
C |
| C | |
AB sin |
(28)
(29)
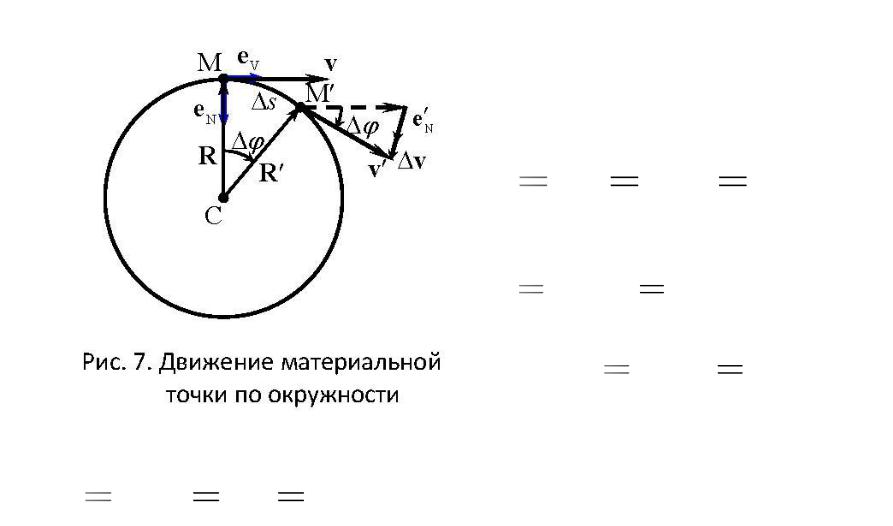
Равномерное движение точки по окружности
Центростремительное (нормальное) ускорение
|
|
|
|
|
|
a |
|
|
a |
|
V 2 |
2R |
(30) |
|||
|
|
|
|
|
|
цс |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n |
|
|
R |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
V |
|
2 R |
|
R |
|
|
(31) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
T |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 n |
(32) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
T |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dN |
|
1 |
|
|
|
|
T – период вращения |
|
|||||||
n |
|
(Гц) (33) |
|
|
– частота вращения |
|||||||||||
dt |
T |
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Равноускоренное вращение
|
t |
|
|
|
|
dt |
0 |
t |
(33) |
|
0 |
|
|
|
|
|
a |
|
t |
t |
|
dt |
( 0 |
|
0 |
0 |
|
t |
t |
S |
vdt |
Rdt |
|
0 |
o |
dV |
R d |
R |
|
(34) |
||
dt |
|
dt |
|
|
|
|
t)dt |
0 |
0t |
t 2 |
(35) |
||
2 |
||||||
|
|
|
|
|
||
t |
d |
|
|
|
|
|
R |
dt |
R |
2 RN |
(36) |
||
|
||||||
0 |
dt |
|
|
|
||
|
|
|
|
|
||
N – число оборотов
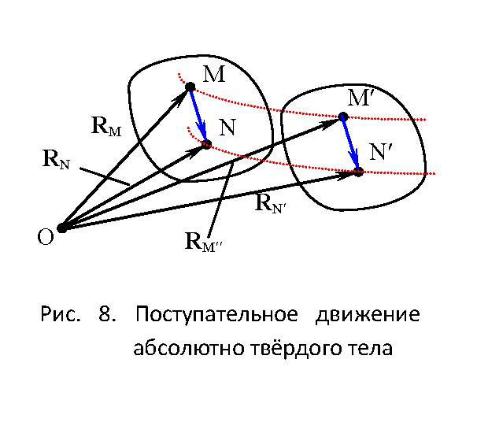
Кинематика твёрдого тела
Существует два типа движения абсолютно твёрдого тела – поступательное и вращательное
Поступательным называется такое движение, при котором прямая, проведенная через две произвольные точки тела, остаётся параллельной самой себе
Из условия абсолютной твёрдости следует
R |
MN |
R |
N |
R |
M |
const |
(37) |
|
|
|
|
|
Из (37) следует, что скорости и ускорения точек M и N должны быть равны
V |
dRN |
|
|
|
dRM |
V |
|
(38) |
||||||
|
|
|
|
|
|
|||||||||
N |
|
|
dt |
|
|
dt |
M |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
a |
|
|
dVN |
|
|
dVM |
a |
|
|
(39) |
||||
N |
|
|
M |
|
||||||||||
|
|
|
dt |
|
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
Все точки абсолютно |
твёрдого |
|
тела движутся по |
|||||||||||
одинаковым траекториям, которые можно совместить друг с другом. Такие траектории называются конгруэнтными
Для описания поступательного движения абсолютно твёрдого тела достаточно знать движение любой одной выбранной точки. Обычно в качестве такой точки выбирается центр масс тела
Вращение твёрдого тела
Произвольное движение тела можно рассматривать как последовательное применение поступательного движения, а затем вращательного движения вокруг центра масс, или сначала как вращение вокруг центра масс, а затем поступательное движение повёрнутого тела.
Это означает, что поступательное и вращательное движение являются независимыми. Иначе говоря, операции поступательного движения и вращения являются коммутативными
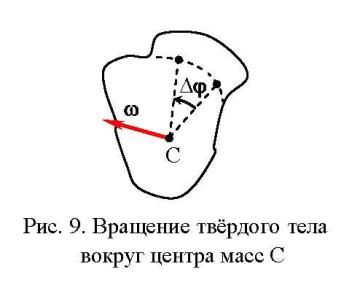
За бесконечно малое время t точка тела проходит траекторию по поверхности сферы с центром в центре масс, вокруг которого вращается всё тело.
Эта траектория является дугой большого круга этой сферы с углом раствора .
Вращение тела вокруг точки сводится к мгновенному вращению вокруг оси, проходящей через центр C этого круга перпендикулярно ему.
Мгновенное вращение происходит в плоскости