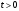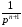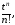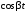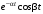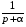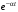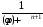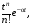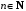3
.docxФормула Остроградского – Гаусса:
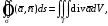
где
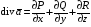 – дивергенция
векторного поля.
– дивергенция
векторного поля.
Если переменные x, y, z в тройном интеграле заменяют цилиндрическими координатами
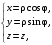
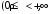
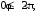
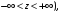 то
используют формулу
то
используют формулу
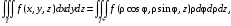
где T* – область в цилиндрической системе координат, соответствующая области T в декартовой системе координат.
Циркуляцией
векторного поля
 вдоль замкнутого контура L
называется криволинейный интеграл
вдоль замкнутого контура L
называется криволинейный интеграл
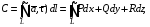
где
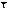 – единичный вектор, направленный по
касательной к кривой L
в направлении ее обхода.
– единичный вектор, направленный по
касательной к кривой L
в направлении ее обхода.
Положительным направлением обхода замкнутого контура называется направление, при котором линия интегрирования обходится против хода часовой стрелки, а отрицательным – по ходу часовой стрелки.
Если
кривая L
задана параметрически в пространстве
уравнениями
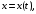

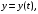 где
где
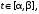 то
то

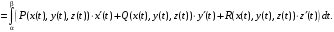
Задания 181 – 190. Числовым рядом называется выражение вида
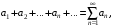
где
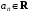
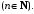
Сумма
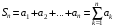
называется n-й частичной суммой.
Если существует предел
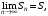
то
ряд называется сходящимся,
а S
– его суммой; пишут:

Если
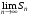 не существует, то ряд называется
расходящимся.
не существует, то ряд называется
расходящимся.
Необходимый
признак сходимости.
Если
ряд
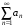 сходится, то
сходится, то
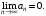
Следствие
необходимого признака сходимости.
Если
 то ряд
то ряд
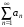 расходится.
расходится.
Признак
сравнения.
Пусть для знакоположительных рядов
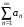 и
и
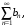 начиная с некоторого n
начиная с некоторого n
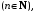 выполняется неравенство
выполняется неравенство
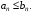
Тогда:
а) из
сходимости ряда
 следует сходимость ряда
следует сходимость ряда
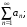
б) из
расходимости ряда
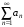 следует расходимость ряда
следует расходимость ряда
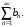
Предельный
признак сравнения.
Если для знакоположительных рядов
 и
и
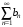 существует
существует
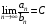
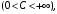
то оба эти ряда сходятся или оба расходятся.
Для исследования по признаку сравнения или предельному признаку сравнения часто используют следующие ряды:
а) ряд
 сходящийся при
сходящийся при
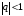 и расходящийся при
и расходящийся при
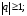
б) ряд
Дирихле
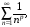 сходящийся при
сходящийся при
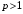 и расходящийся при
и расходящийся при
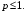
Предельный
признак Д’Аламбера.
Пусть для знакоположительного ряда
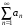 существует
существует
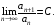
Тогда:
а) при
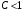 ряд сходится;
ряд сходится;
б) при
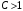 ряд расходится.
ряд расходится.
Предельный
признак Коши.
Пусть для знакоположительного ряда
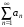 существует
существует
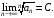
Тогда:
а) при
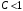 ряд сходится;
ряд сходится;
б) при
 ряд расходится.
ряд расходится.
Если
в предельных признаках Д’Аламбера и
Коши получаем
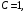 то нужны дополнительные исследования
по другим признакам.
то нужны дополнительные исследования
по другим признакам.
При использовании предельного признака Коши часто применяют формулу
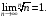
Иинтегральный
критерий сходимости.
Пусть члены ряда
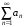 имеют вид
имеют вид
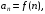 где
где
 – неотрицательная монотонно убывающая
на
– неотрицательная монотонно убывающая
на
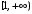 функция. Ряд сходится (расходится) тогда
и только тогда, когда сходится (расходится)
несобственный интеграл
функция. Ряд сходится (расходится) тогда
и только тогда, когда сходится (расходится)
несобственный интеграл
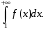
Задания 191 – 200.
Знакопеременный числовой ряд
 называется абсолютно
сходящимся,
если сходится ряд
называется абсолютно
сходящимся,
если сходится ряд

Абсолютно сходящийся ряд сходится.
Знакопеременный ряд называется условно сходящимся, если он сходится, но не абсолютно.
Знакопеременный ряд называется знакочередующимся, если любые два его соседних члена имеют разные знаки:
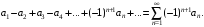
где
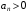
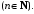
Признак
Лейбница.
Если для знакочередующегося ряда
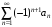 выполняются условия:
выполняются условия:
1) 
2) 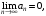
то ряд сходится.
Следствие
признака Лейбница.
Если
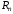 – n-я
частичная сумма знакочередующегося
ряда
– n-я
частичная сумма знакочередующегося
ряда
 то
то

Степенным рядом называется ряд вида
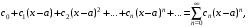
где

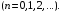
Радиусом сходимости степенного ряда называется число r, которое находят по формулам:
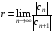 или
или
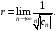
Ряд
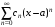 сходится, причем абсолютно, на интервале
сходимости
сходится, причем абсолютно, на интервале
сходимости
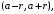 где
где
 и расходится на
и расходится на

Для определения области сходимости степенного ряда следует:
1) найти его радиус сходимости;
2) определить интервал сходимости с центром в точке a;
3) выяснить вопрос о сходимости ряда в граничных точках этого интервала, подставив их вместо x в заданный ряд.
Задания 201 – 210. Степенной ряд вида

называется
рядом
Тейлора функции

Рядом
Маклорена функции
 называется ряд Тейлора вида
называется ряд Тейлора вида

Имеют место разложения элементарных функций в ряд Маклорена:
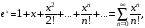
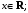
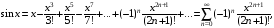
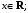
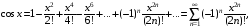
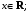


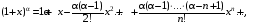
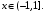
Задания 211 – 220.
Рядом Фурье
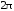 -периодической
функции
-периодической
функции
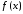 называется функциональный ряд вида
называется функциональный ряд вида
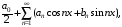
где коэффициенты вычисляют по формулам:
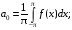
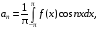
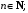
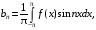
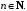
Теорема
Дирихле.
Пусть
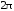 -периодическая
функция
-периодическая
функция
 является кусочно-гладкой на
является кусочно-гладкой на
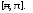 Тогда ее ряд Фурье сходится к
Тогда ее ряд Фурье сходится к
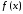 в каждой точке непрерывности
и к
в каждой точке непрерывности
и к
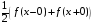 в точке разрыва, где
в точке разрыва, где
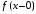 и
и
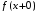 –
соответственно левосторонний и
правосторонний пределы функции
–
соответственно левосторонний и
правосторонний пределы функции
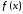 в точке x.
в точке x.
Задания 221 – 230.
Рядом Лорана
функции
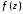 называется ряд вида
называется ряд вида
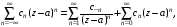
где
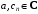
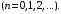
Ряд
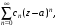 называемый правильной
частью ряда
Лорана, сходится в круге
называемый правильной
частью ряда
Лорана, сходится в круге
 Ряд
Ряд
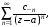 называемый главной
частью ряда
Лорана, сходится вне круга
называемый главной
частью ряда
Лорана, сходится вне круга

Функция
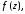 аналитическая в кольце
аналитическая в кольце
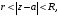 разлагается в этом кольце в абсолютно
сходящийся ряд Лорана
разлагается в этом кольце в абсолютно
сходящийся ряд Лорана

Имеет место разложение:
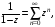
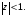
Задания 231 – 240.
Функция называется аналитической
в точке, если
существует некоторая окрестность этой
точки, в которой функция однозначна и
дифференцируема. Функция
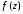 называется аналитической
в области D,
если она аналитическая в каждой точке
этой области.
называется аналитической
в области D,
если она аналитическая в каждой точке
этой области.
Изолированной
особой точкой функции
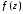 называется точка, в некоторой проколотой
окрестности которой функция
называется точка, в некоторой проколотой
окрестности которой функция
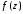 аналитична, но не аналитична в самой
этой точке (или не определена в ней).
аналитична, но не аналитична в самой
этой точке (или не определена в ней).
Изолированная
особая точка a
функции
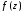 называется устранимой,
если ряд Лорана функции имеет вид
называется устранимой,
если ряд Лорана функции имеет вид

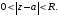
Тогда
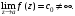
Изолированная
особая точка a
функции
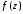 называется полюсом
k-го
порядка,
если
называется полюсом
k-го
порядка,
если
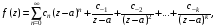
где
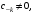
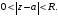 Тогда
Тогда
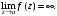
При
 полюс называют простым
полюсом.
полюс называют простым
полюсом.
Изолированная
особая точка a
функции
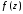 называется существенно
особой, если
называется существенно
особой, если
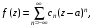
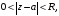
и
бесконечное количество элементов
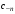
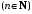 отлично от нуля. Тогда
отлично от нуля. Тогда
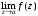 не существует.
не существует.
Вычетом
функции
 в особой точке a
называется коэффициент при первой
отрицательной степени ряда Лорана
функции
в особой точке a
называется коэффициент при первой
отрицательной степени ряда Лорана
функции
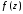 в проколотой окрестности точки a.
Пишут:
в проколотой окрестности точки a.
Пишут:
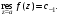
Если a – простой полюс, то
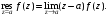
Если a – полюс k-го порядка, то
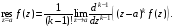
Основная
теорема о вычетах.
Если функция
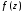 – аналитическая в односвязной области
D,
кроме конечного числа особых точек, Γ
– замкнутая положительно ориентированная
кривая, расположенная в D
и содержащая внутри себя особые точки
– аналитическая в односвязной области
D,
кроме конечного числа особых точек, Γ
– замкнутая положительно ориентированная
кривая, расположенная в D
и содержащая внутри себя особые точки
 то
то
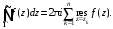
Задания 241 – 250.
Свойство
линейности.
Если
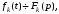
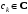
 то
то
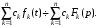
Теорема
подобия.
Если
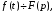
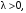 то
то

Теорема
смещения.
Если

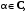 то
то

Таблица основных операционных соотношений.
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

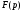
 при
при

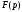
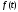 при
при