КР по ТЭЦ

Министерство образования Республики Беларусь

Учреждение образования

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»

Институт информационных технологий

Специальность: Промышленная электроника

КОНТРОЛЬНАЯ РАБОТА

По курсу: Теория электрических цепей

Вариант №6

Студент-заочник 2 курса

Группы № 481971

Гавриленков Егор Олегович

Проверил

Минск, 2016

Изобразим схему согласно заданному варианту.

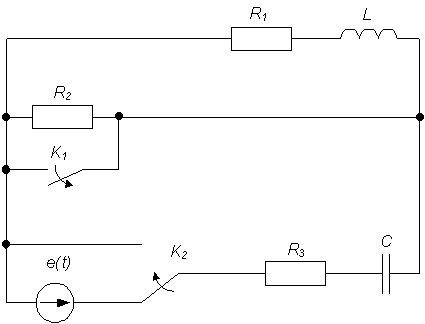
Рис.1 Принципиальная схема цепи.

1. Определим классическим методом напряжение на емкости и ток через индуктивность исходной схемы (рис.1) при размыкании ключа К1.

1.1. Рассчитаем параметры схемы в момент коммутации.

1.1.1. Определим независимые начальные условия (ННУ):

Определим комплексные сопротивления ветвей:

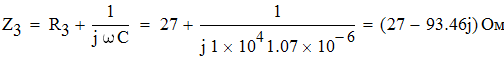
Определим ток через источник ЭДС:

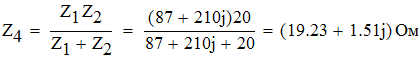
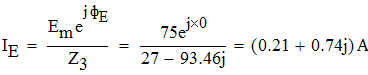
Определим ток через индуктивность:

Определим ток через емкость:

Определим напряжение на емкости:

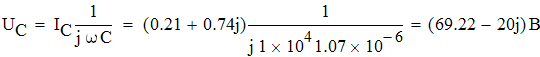
1.1.2. Определим зависимые начальные условия (ЗНУ) для схемы в момент коммутации (рис. 2):

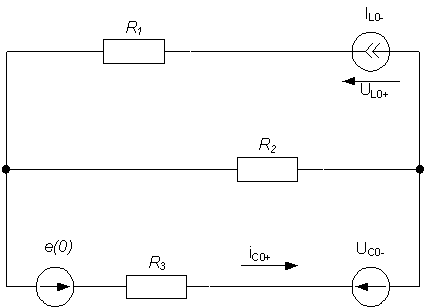
Рис.2 Эквивалентная схема цепи при t=0.

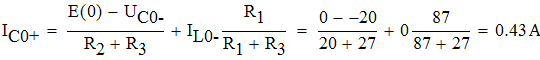
1.2. Определим закон изменения напряжения на емкости и тока через индуктивность. Для этого используем искусственный прием - для послекоммутационной схемы разорвем произвольно выбранную ветвь и относительно разрыва найдем входное сопротивление Zвх(p) (полагая Zист=0), где p=jω.

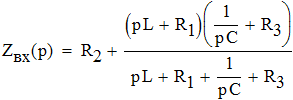
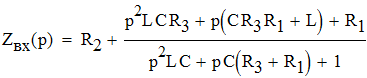
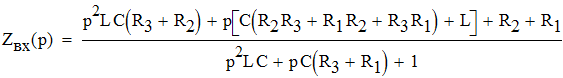
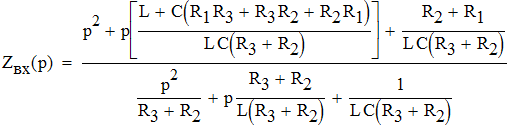
Решив уравнение Z_вх(p)=0 найдем его корни, которые определят закон изменения переходного процесса. Решая уравнение Z_вх(p)=0 приходим к квадратному p²+ap+b=0, где:

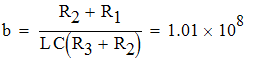
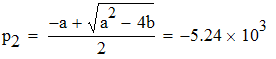
1.3. Рассчитаем принужденную составляющую напряжения на емкости и тока через индуктивность для послекоммутационной схемы (рис. 3).

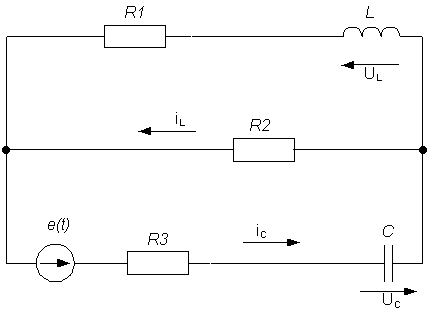
Рис.3 Принципиальная схема цепи после коммутации.

Определим комплексные сопротивления ветвей:

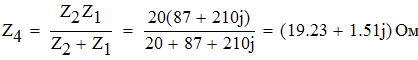
Определим ток через источник ЭДС:

Определим ток через индуктивность:

Определим напряжение на индуктивности:

Определим ток через емкость:

Определим напряжение на емкости:

1.4. Определим закон изменения тока через индуктивность и напряжения на емкости.

1.4.1. Определим закон изменения тока через индуктивность:

где:

Найдем коэффициенты А₁, А₂ продифференцировав выражение для тока через индуктивность и составив систему уравнений.

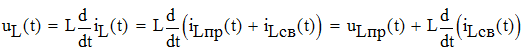
Положим t=0 и найдем А₁, А₂.

Отсюда находим A₁ и A₂ :

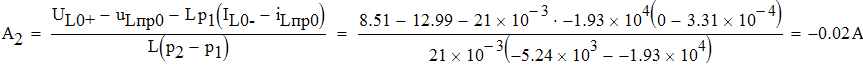
Построим график переходного процесса тока через индуктивность (рис. 4):

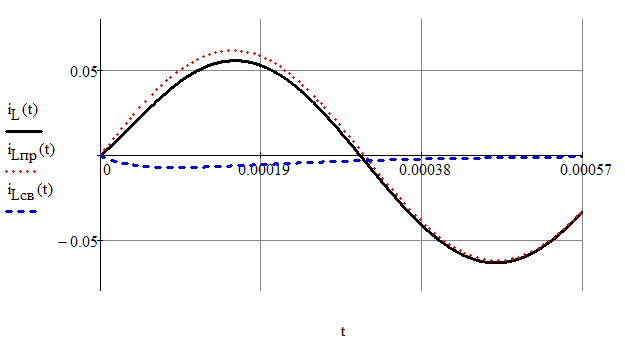
Рис.4 График переходного процесса тока через индуктивность.

1.4.2. Определим закон изменения напряжения на индуктивности:

Введем новые переменные B₁ и B₂:

Построим график переходного процесса напряжения на индуктивности (рис.5):

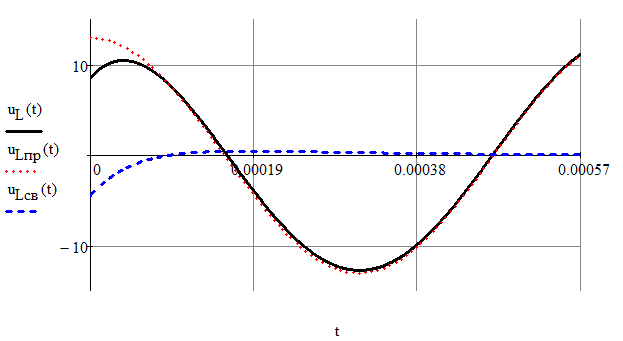
Рис.5 График переходного процесса напряжения на индуктивности.

1.4.3. Определим закон изменения напряжения на емкости:

где:

Найдем коэффициенты D₁, D₂ продифференцировав выражение для напряжения на емкости и составив систему уравнений.

Положим t=0 и найдем D₁, D₂.

Отсюда находим D₁, D₂:

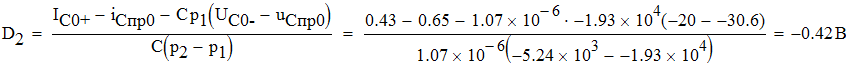
Построим график переходного процесса напряжения на емкости (рис.6):

Рис.6 График переходного процесса напряжения на емкости.

1.4.4. Определим закон изменения тока через емкость:

Введем новые переменные E₁ и E₂:

Построим график переходного процесса тока через емкости (рис.7):

Рис.7 График переходного процесса тока через емкость.

Сведем результаты расчета в таблицу:

2. Определим операторным методом напряжение на емкости и ток через индуктивность при постоянном напряжении ЭДС для схемы на рис. 8.

2.1. Определим независимые начальные условия (ННУ):

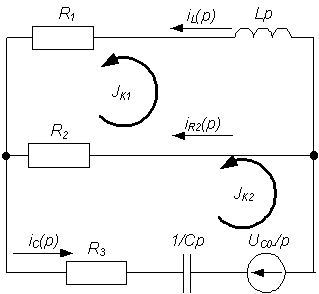
Рис.8 Принципиальная схема цепи после коммутации.

2.2. Найдем ток через индуктивность и напряжение на емкости с использованием метода контурных токов:

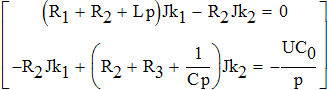
Решая систему определяем значения контурных токов:

Найдем искомые токи ветвей:

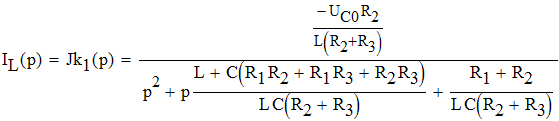
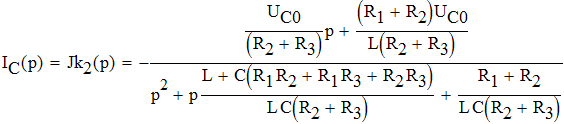
2.2.1. Определим закон изменения тока через индуктивность. Для этого упростим выражение для тока через индуктивности в операторной форме.

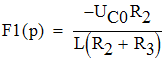
Найдем корни знаменателя i_L(p). Решая уравнение F2(p)=0 приходим к квадратному p²+ap+b=0, где:

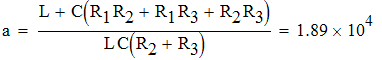
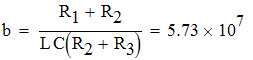
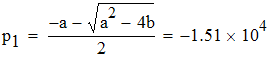
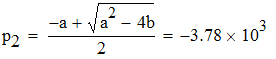
По теореме разложения найдем оригинал операторного тока i_L(p):

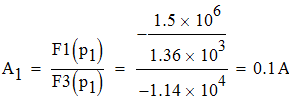
Построим график переходного процесса тока через индуктивность (рис. 9):

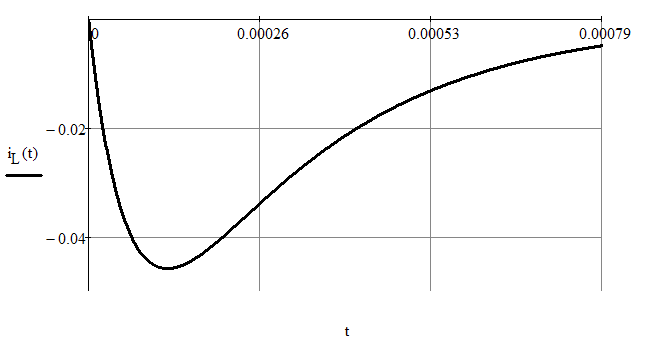
Рис.9 График переходного процесса тока через индуктивность.

2.2.2. Определим закон изменения напряжения на емкости. Для этого воспользуемся рассчитанными ранее методом контурных токов значениями:

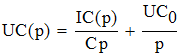
2.2.3. Определим закон изменения напряжения на емкости. Для этого упростим выражение для напряжения на емкости в операторной форме.

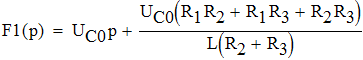
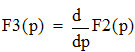
По теореме разложения найдем оригинал операторного напряжения u_С(p):

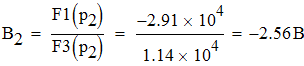
Построим график переходного процесса напряжения на емкости (рис.10):

Сведем результаты расчета в таблицу:

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.Применение Mathcad в электротехнических расчетах: метод. Пособие к выполнению контр. Заданий / В.М. Коваленко, И.Л. Свито. – Минск: БГУИР, 2008. – 52 с. : ил.

2.Теория электрических цепей: метод. Пособие к выполнению контрольных заданий для студ. всех спец. БГУИР заоч. Формы обуч. / Л.Ю. Шилин [и др.]. – Минск: БГУИР, 2010. – 83 с.: ил.