13. Определение дисперсионного анализа (да). Основные понятия и виды да.
ДА – статистический метод анализа результатов наблюдений, зависящих от различных одновременно действующих факторов, основанный на сравнении оценок дисперсий соответствующих групп выборочных данных.
фактор – различные, независимые, качественные показатели, влияющие на изучаемые признаки. Обозначаются факторы А,В,С… факторы, контролируемые и измеряемые в процессе исследования называются регулируемыми.
Признаки, изменяющиеся под воздействием тех или иных факторов, называют результативными. Для их обозначения используют X, Y, Z.
Основная идея дисперсионного анализа состоит в сравнении факторной дисперсии, определяемой влиянием регулируемого фактора и остаточной дисперсии, обусловленной действием неконтролируемых и случайных причин. С помощью F-критерия устанавливается влияние фактора на признак.
14. Условия проведения дисперсионного анализа (да). Однофакторный да.
Условия применения дисперсионного анализа к выборочным данным:
выборочные данные должны быть взяты из совокупностей с нормальным законом распределения.
дисперсии всех совокупностей должны быть равны.
Схема проведения однофакторного дисперсионного анализа:
Полученные данные заносятся в таблицу, где в верхней части по горизонтали указываются градации регулированного фактора А, а по вертикали – номера испытаний. Данные группируются по столбцам, каждый из которых соответствует одному уровню фактора.
Вычисляются групповые выборочные средние:
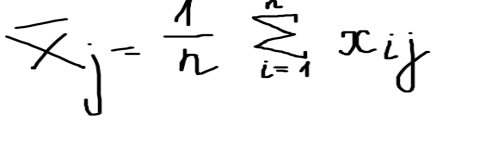
и общее выборочное среднее, где N= n*m :
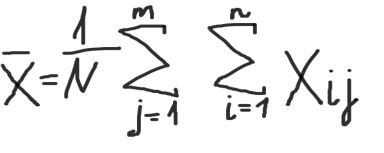
Расчитывается межгрупповая сумма квадратов, которая показывает отклонение групповых средних хj от общего выборочного среднегои определяется влиянием различных уровней фактора А:
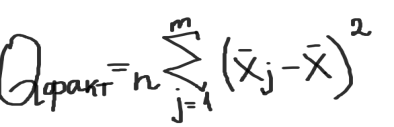
определяется внутригрупповая сумма квадратов, которая показывает отклонение наблюдений хij от соответствующих групповых средних хj и учитывает разбросы значений хij внутри каждой из групп, вызванные случайными признаками при постоянном значении фактора А:
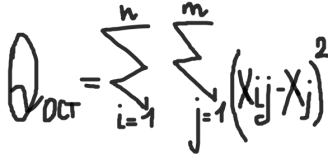
Общая сумма квадратов:
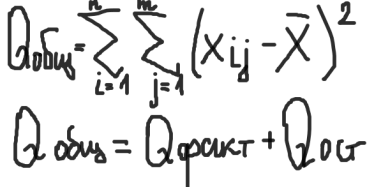
Определение числа степеней свободы для факторного отклонения: fфакт= m-1,
для остаточной вариации: fост= N-m,
для общего: fобщ= N-1 или fобщ=fфакт+fост
Факторная выборочная дисперсия:
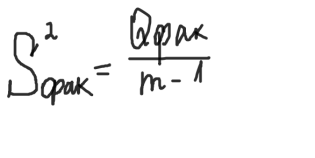
Остаточная выборочная дисперсия:
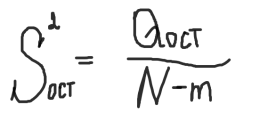
Общая дисперсия:
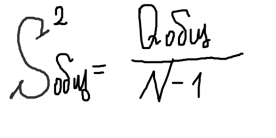
6) определяется эффективность влияния фактора А на результативный признак. Для этого сравнивают расчетный критерий фишера и его табличное значение. Влияние фактора А считается значимым на уровне значимости α, если выполняется неравенство:
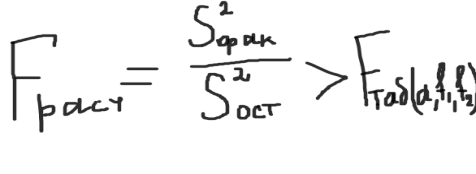
Значение Fтабл(α,f1,f2) находится по таблице для заданного уровня значимости. Если неравенство не выполняется, то влияние фактора А на результативный признак считается несущественным.
15. Анализ двухфакторных комплексов. Понятие о многофакторном комплексе.
Влияние 2ух факторов А и В одновременно действующие на признак х. Последовательность этапов двухфакторного анализааналогично схеме однофакторного анализа. Однако в этом анализе необходимо кроме оценки влияния каждого фактора учитывать их совместное действие на результативный признак.Он проводится по схеме:
Результаты экспериментов заносятся в таблицу, где по горизонтали указывается градации фактора А, а по вертикали – фактора В. На пересечении строки и столбца заносится результат признака хijк при i-м значении фактора А и j-м значении фактора В, а к- номер испытания (изменяется от 1 до q)
вычисляются внутригрупповые выборочные средние для каждой пары уровней А и В.
- вычисляются групповые выборочные средние при постоянном значении фактора А
- групповые выборочные значения при постоянном значении фактора В
- общее выборочное среднее
3) Расчитываются межгрупповые суммы квадратов отклонений
- для фактора А
-для фактора В
-для совместного действия факторов А и В
- внутригрупповая сумма квадратов отклонений для прочих факторов (Qост)
-общая сумма квадратов отклонений
4) Нахождение числа степеней свободы (для влияния фактора А, В, для совместного влияния факторов А и В,для прочих факторов(Qост) и для общего варьирования(Qобщ))
5) Определяются выборочные дисперсии как отношение сумм квадратовотклонений к соответствующим числам степеней свободы
6) Определяется значимость влияния фактора А,В и их совместного действия на результативный признак. Для этого расчетное значение критерия Фишера сравнивается с его табличной величиной. Влияние фактора А считается значимым на уровне значимости α, если выполняется неравенство:
Значение Fтабл(α, f1, f2) находится по таблице фишера-снедекора для заданного значения уровня значимости α и числа степеней свободы f1 и f2. Если какое-либо неравенство не выполняется, то влияние фактора на результативный признак считается несущественным.