3. Система параллельных сил
Решение. При опрокидывании тело будет поворачиваться вокруг точки опрокидывания.
Выберем декартову систему координат Cxy так, чтобы начало координат совпало с центром тяжести тела, а одна из осей была параллельна поверхности, на которой стоит тело. Разложим вес тела P на проекции вдоль выбранных осей Px и Py (рис. 3.12, б):
Px = P sin α, Py = P cos α.
При падении тела точкой опрокидывания будет точка А (рис. 3.12, б). При равновесии тела сумма моментов всех сил относительно точки опрокидывания должна быть равной нулю:
∑M A = 0, Py b − Px a = 0, P b cos α − P a sin α = 0,
откуда tgα = bа, α = arctg bа.
Тело находится в равновесии до тех пор, пока линия действия веса тела P не совпадет с линией n −n , проходящей через центр тяжести тела (точка С) и точку опрокидывания А. В момент совпадения этих линий тело будет находиться в состоянии неустойчивого равновесия.
Ответ: при угле наклона поверхности α′ = α тело будет находиться в состоянии неустойчивого равновесия, при α′>α тело опрокинется.
3.5. Распределенные силы
Вмеханике рассматривают силы, приложенные к твердому телу
вкакой-либо его точке. Такие силы называют сосредоточенными.
Вдействительности силы бывают приложены к какой-либо части тела. Так как все аксиомы и теоремы статики формулируются для сосредоточенных сил, приложенных к твердому телу, то необходимо рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших, наиболее часто возникающих случаях.
Распределенные силы характеризуются в каждой точке числовым значением и направлением вектора интенсивности этой нагрузки.
Величины распределенных сил задаются в каждой точке их q (Н/м). Сила действует на единицу длины.
77
И. В. Богомаз. Механика
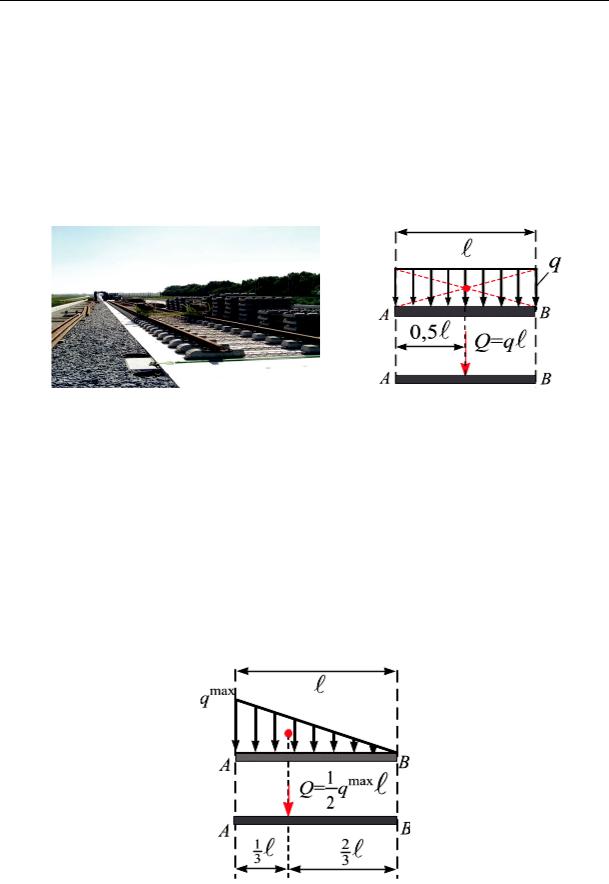
Равномерно-распределенная нагрузка. Пример равномерно-
распределенной нагрузки приведен на рис. 3.13, а. Если сила распределена равномерно (интенсивность постоянная), то ее равнодействующую вычисляют, умножая интенсивность на соответствующую площадь или объем. Пусть на участке AB, длина которого ℓ (рис. 3.13, б), равномерно распределена нагрузка интенсивностью q. Равнодействующая Q направлена параллельно равномерно-распределенной нагрузке, приложена в середине участка AB и равна Q = q · ℓ.
а |
б |
Рис. 3.13
Линейно-распределенная нагрузка. На участок AB (рис. 3.14),
длина которого , приложена линейно-распределенная нагрузка интенсивностью qmax. Равнодействующая Q параллельна qmax, приложена
в точку, которая делит участок AB в соотношении 13 : 23 и равна Q = 12 qmax .
Рис. 3.14
78
3. Система параллельных сил
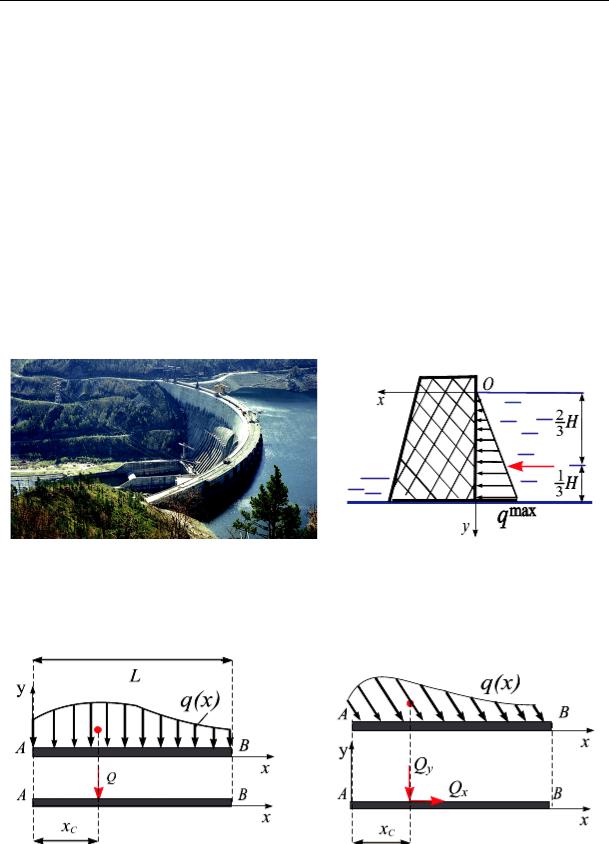
Примером линейно-распределенной нагрузки может служить давление воды на плотину высотой H, изменяющееся с глубиной по линейному от поверхности воды закону q(y) = ky (рис. 3.15, а, б).
Распределенная нагрузка характеризуется равнодействующей, величина которой в общем случае равна
L |
|
Q = ∫q(x)dx. |
(3.8) |
0 |
|
Линия действия равнодействующей Q параллельна распределенным силам и проходит через центр тяжести этой площади (рис. 3.16, а). Вопрос о вычислении центров тяжести площадей будет рассмотрен в главе 5.
а |
б |
Рис. 3.15
а |
б |
Рис. 3.16
79
И. В. Богомаз. Механика
Величину равнодействующей Q, когда параллельные распределенные силы не перпендикулярны поверхности, вычисляют по формуле (3.8) и раскладывают на проекции по осям координат Qx и Qy соответственно (рис. 3.16, б).
80