
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ИЗ МАТЕМАТИКИ
- •1.1. Прямоугольная декартова система координат
- •1.2. Понятие об абсолютно твердом теле и его степенях свободы
- •1.3. Элементы тригонометрии
- •1.4. Векторы
- •1.5. Инерциальная система отсчета
- •2. СТАТИКА
- •2. 1. Аксиомы статики
- •2.2. Теорема о переносе вектора силы вдоль линии действия
- •3. СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ
- •3.1. Приведение к равнодействующей системы параллельных сил, направленных в одну сторону
- •3.2. Приведение к равнодействующей двух сил, направленных в разные стороны
- •3.3. Пара сил
- •3.4. Правило рычага. Момент силы относительно точки
- •3.5. Распределенные силы
- •4. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА И ОСИ
- •4.1. Момент силы
- •4.2. Приведение силы к заданному центру
- •4.3. Условия равновесия произвольной пространственной системы сил
- •4.4. Условия равновесия произвольной плоской системы сил
- •4.5. Вычисление реакций опор конструкций арочного типа
- •5. ЦЕНТР ТЯЖЕСТИ
- •5.1. Центр параллельных сил
- •5.2. Центр тяжести твердого тела
- •5.3. Центр тяжести плоского сечения
- •5.4. Центры тяжести простейших тел
- •5.5. Методы вычисления центров тяжести тел
- •6. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- •6.1. Приведение к равнодействующей силе
- •6.2. Условия равновесия системы сходящихся сил
- •6.3. Равновесие твердого тела под действием трех сил
- •7. КИНЕМАТИКА ТОЧКИ
- •7.1. Траектория, скорость, ускорение
- •7.2. Движение точки в плоскости
- •7.3. Простейшие движения твердого тела
- •8. ДИНАМИКА
- •8.1. Основные законы движения материальной точки
- •8.2. Две основные задачи динамики точки
- •8.3. Теорема об изменении кинетической энергии
- •8.4. Принцип возможных перемещений
- •8.5. Принцип Д’Аламбера. Силы инерции
- •9. ДЕФОРМИРУЕМОЕ ТВЕРДОЕ ТЕЛО
- •9.1. Общие сведения
- •9.2. Классификация нагрузок
- •9.3. Метод сечений. Виды сопротивлений бруса. Построение эпюр
- •10. ПОНЯТИЕ О НАПРЯЖЕНИИ И ДЕФОРМАЦИИ
- •10.1. Напряженное состояние в точке
- •10.2. Интегральные зависимости между внутренними силовыми факторами и напряжениями
- •10.3. Деформации и перемещения. Деформированное состояние в точке
- •11. ОСЕВОЕ РАСТЯЖЕНИЕ И СЖАТИЕ В ПРЕДЕЛАХ УПРУГОСТИ
- •11.1. Основные понятия и зависимости. Условия прочности
- •11.2. Перемещения. Эпюра перемещений. Условие жесткости
- •11.3. Расчеты на прочность и жесткость
- •12. ПЛОСКИЕ СТЕРЖНЕВЫЕ ФЕРМЫ
- •12.1. Общая характеристика и классификация ферм
- •12.2. Методы расчета плоских ферм
- •13. ИЗГИБ БРУСА
- •13.1. Поперечный изгиб
- •13.2. Расчеты на прочность при изгибе
- •13.3. Перемещения при изгибе
- •13.4. Расчет балок на жесткость
- •14. ВНЕЦЕНТРЕННОЕ СЖАТИЕ ИЛИ РАСТЯЖЕНИЕ
- •14.1. Определения. Условия прочности
- •14.2. Ядро сечения
- •15. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
- •15.1. Понятие об устойчивости
- •15.2. Продольный изгиб. Потеря устойчивости
- •15.3. Формула Эйлера для вычисления критической силы шарнирно закрепленного стержня
- •15.5. Критическое напряжение. Гибкость стержня
- •15.6. Продольный изгиб за пределом пропорциональности. Формула Ясинского
- •15.7. Диаграмма критических напряжений
- •15.8. Принципы рационального проектирования сжатых стержней
- •ОГЛАВЛЕНИЕ
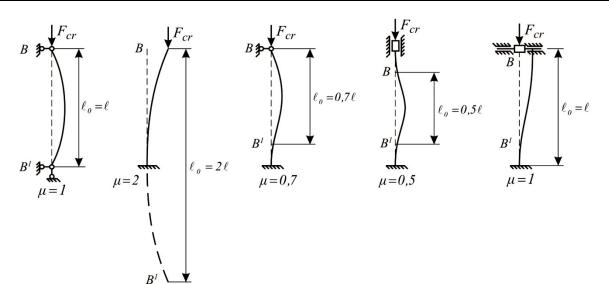
15. Устойчивость сжатых стержней
а |
б |
в |
г |
д |
Рис. 15.5
Итак, коэффициент μ может быть определен исходя из геометрии задачи.
Если концы стержня закреплены так, что приведенная длина 0
оказывается одинаковой для обеих главных плоскостей, то при вычислении Fcr следует брать наименьший момент инерции поперечного сечения (см. формулу (15.11).
Если же закрепление концов стержня в плоскостях Oxz и Oyz таково, что коэффициенты приведенной длины различны и равны μ1 и μ2, соответственно, то критическая сила определяется как меньшая из двух возможных в главных плоскостях:
F = |
π2 EJ y |
и F = |
π2 EJ |
x |
. |
(15.14) |
||
(μ )2 |
(μ |
|
) |
|
||||
1 |
2 |
2 |
2 |
|
|
|||
|
1 |
|
|
|
|
|
|
|
15.5. Критическое напряжение. Гибкость стержня
Пределы применимости формулы Эйлера. Нормальное напря-
жение σcr в поперечном сечении сжатого стержня, вызываемое критической силой, называется критическим напряжением. С учетом
(15.13), имеем
325
И. В. Богомаз. Механика
|
F |
π2 EJ |
x |
|
|
π2 E |
|
|
||
σcr = |
cr |
= |
|
= |
|
|
|
, |
(15.15) |
|
|
(μ )2 A |
|
|
2 |
||||||
|
A |
|
μ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ix |
|
|
|
где ix = Jx  A − радиус инерции поперечного сечения. Введем обозначение
A − радиус инерции поперечного сечения. Введем обозначение
λ = |
μ , |
(15.16) |
|
ix |
|
где λ – гибкость стержня, безразмерная геометрическая характеристика, определяемая размерами стержня и способом его закрепления.
Окончательно формула для критического напряжения выглядит
так:
σcr = |
π2 E |
|
λ2 . |
(15.17) |
При выводе формулы Эйлера была использована зависимость (15.2), полученная на основе закона Гука. Отсюда следует, что формула Эйлера справедлива лишь в пределах применимости закона Гука, т. е. при условии, что критическое напряжение не превышает предела пропорциональности материала стержня:
σcr = |
π2 E |
≤ σpr . |
(15.18) |
λ2 |
Отсюда значение гибкости, которое соответствует этому условию, составляет
λ ≥ π E σpr . |
(15.19) |
Величину, стоящую в правой части этого неравенства, обозначим λпред и назовем предельной гибкостью
λпред = π E σpr . |
(15.20) |
Предельная гибкость зависит только от механических свойств материала и имеет постоянное значение. Так для стали марки ВСт3 при
326

15. Устойчивость сжатых стержней
E = 2,06 105 МПа и σpr = 200–210 МПа по формуле (15.20) λпред ≈100 ;
для древесины сосны и ели (при E = 10 МПа и σpr = 20 МПа) λпред = 70. Тогда условие применимости формулы Эйлера имеет вид
λ ≥ λпред , |
(15.21) |
т. е. формула Эйлера применима только к упругим стержням, когда гибкость стержня больше или равна предельной гибкости для материала, из которого он изготовлен.
Стержни, для которых выполняется условие (15.21), называются стержнями большой гибкости.
15.6. Продольный изгиб за пределом пропорциональности. Формула Ясинского
Формула Эйлера применима при λ ≥ λпред, т. е. только в случае упругих стержней. Для стержней с гибкостью меньше предельной λпред , она дает завышенные значения критической силы. Поэтому ис-
пользование формулы Эйлера для стержней, теряющих устойчивость за пределом упругости, является недопустимым.
Теоретическое решение задачи об устойчивости за пределом пропорциональности сложно, поэтому обычно пользуются эмпирическими формулами, полученными в результате обработки большого количества опытных данных.
Наиболее простой является линейная зависимость, предложенная в начале ХХ в. немецким ученым Л. Тетмаером и независимо от него профессором Петербургского института инженеров путей сообщения Ф. С. Ясинским:
σcr = a −b λ, |
(15.22) |
где a и b – эмпирические коэффициенты, зависящие от материала стержня и имеющие размерность напряжения. Например, для стали марки ВСт3 их значения таковы: а = 310 МПа, b = 1,14 МПа.
Для чугуна пользуются параболической зависимостью
σcr = a −bλ+cλ2 .
327

И. В. Богомаз. Механика
Соответствующая критическая сила по формуле Ясинского находится так:
Fcr = A(a −b λ) . |
(15.23) |
Условие применимости формулы Ясинского. Формулой Ясин-
ского (15.22) можно пользоваться при условии, если значение σcr, вычисленное по этой формуле, не превышает предела σy текучести для пластичного материала и предел σuc прочности при сжатии для хрупкого материала. Обозначим в формуле (15.22) через λ0 значение гибкости, при котором σcr = σy для пластичного материала и σcr = σuc для хрупкого материала.
Тогда условие применимости формулы Ясинского можно записать в виде
λ0 ≤ λ < λпред. |
(15.24) |
Стержни, для которых выполняется условие (15.24), называются стержнями средней гибкости. Для стали марки ВСт3 с параметрами σpr = 200 МПа, σy = 240 МПа по формуле (15.22) получим λ0 ≈ 60.
Стержни, у которых λ < λ0, называются стержнями малой гибкости. Они могут разрушиться не в результате потери устойчивости, а при центральном сжатии. Для них критическое напряжение считается постоянным: σcr = σy или σcr = σuc.
15.7. Диаграмма критических напряжений
В зависимости от гибкости сжатые стержни делятся на три категории:
1. Стержни большой гибкости (λ ≥ λпред), для которых расчет ведется по формуле Эйлера. В системе координат σcr – λ зависимость
σcr = π22E может быть представлена гиперболической кривой.
λ
2. Стержни средней гибкости (λ0 ≤ λ ≤ λпред) рассчитываются на устойчивость по эмпирической формуле Ясинского (15.22). Для них зависимость линейна:
σcr = a −b λ.
328
15. Устойчивость сжатых стержней
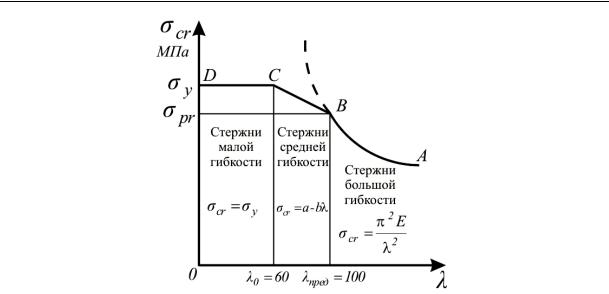
Рис. 15.6
3. Стержни малой гибкости (λ < λ0) рассчитываются не на устойчивость, а на прочность. Для них значение σcr постоянно (σy или σuc).
На рис. 15.6 показана диаграмма зависимости критических напряжений от гибкости сжатого стержня для стали ВСт3, которая состоит из трех частей:
•гиперболы Эйлера АВ при λ ≥ 100;
•наклонной прямой Ясинского ВС при 60 ≤ λ < 100;
•горизонтальной прямой CD при λ0 < 60.
График показывает, что по мере возрастания гибкости критическое напряжение стремится к нулю. При гибкости λ > 100 стержень теряет устойчивость в упругой стадии. Для значений λ < 100 пунктирной линией показано продолжение гиперболы Эйлера в области ее неприменимости (за пределом упругости). Из графика видно, что для стержней средней и малой гибкости формула Эйлера дает сильно завышенные значения критических напряжений.
При гибкости 60 < λ < 100 стержень теряет устойчивость в упру- го-пластической стадии (наклонная прямая ВС). Горизонтальная прямая CD соответствует напряжению, равному пределу текучести.
Применение формул Эйлера и Ясинского позволяет решать задачи устойчивости сжатых стержней на всем интервале значений гибкостей, которые встречаются в строительной практике.
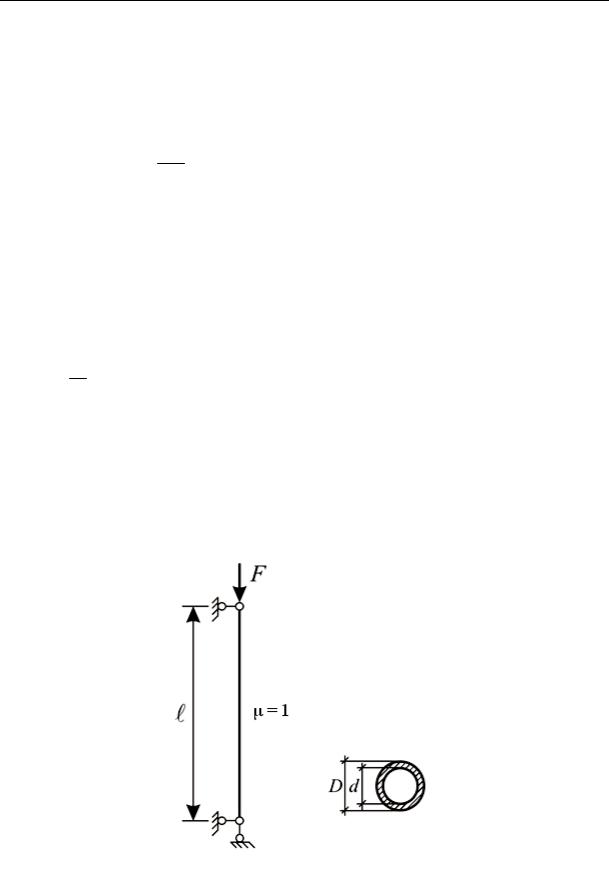
Пример 15.1. Стальной стержень круглого трубчатого сечения D = 10 см и d = 7 см при длине = 3, 2 м имеет шарнирно закрепленные
329
И. В. Богомаз. Механика
концы (рис. 15.7). Вычислить величину допускаемого сжимающего усилия F, если требуемый коэффициент запаса устойчивости K = 3.
Материал стержня – сталь марки ВСт3 с пределом пропорциональности σpr = 210 МПа и модулем упругости E = 2 105 МПа.
Решение. Величину допускаемой силы F найдем исходя из условия устойчивости F ≤ FKcr , предварительно вычислив критическую силу Fcr,
формулудлякоторойвыберемвзависимостиотгибкостистержня. Определяем геометрические характеристики поперечного сече-
ния стержня:
•площадь сечения
А= πD4 2 (1−α2 )= π 104 2 (1−0,72 )= 40 см2 ,
где α = Dd ;
•осевой момент инерции сечения относительно любой оси
J = π64D4 (1−α4 )= π64104 (1−0,74 )= 373 см4 ;
Рис. 15.7
330

15. Устойчивость сжатых стержней
• радиус инерции сечения
i = |
J |
= |
373 |
= 3,05 см. |
|
A |
40 |
||||
|
|
|
Устанавливаем гибкость стержня и выбираем формулу для критической силы.
λ = |
μ |
= |
1 320 |
=105. |
|
i |
|
3,05 |
|
Предельная гибкость для материала стержня
λпред = π |
E |
= 3,14 |
2,1 105 |
=100. |
|
σpr |
210 |
||||
|
|
|
Так как λ = 105 > λпред = 100, то следует взять формулу Эйлера. Вычисляем величину критической силы:
F |
= |
π2 E J |
= |
3,142 2,1 1011 373 10−8 |
= 754кН. |
|
(μ )2 |
(1 3, 2)2 |
|||||
cr |
|
|
|
Вычисляем значение допускаемой силы:
F ≤ FКcr = 7543 = 251кН.
Ответ: допускаемое значение сжимающей силы F ≤ 251 кН.
Пример 15.2. Двутавровый стержень № 14, имеющий длину =1,8 м, нагружен продольной сжимающей силой F = 200 кН. Один конец стержня оперт шарнирно, другой защемлен (рис. 15.8). Определить величину коэффициента запаса устойчивости K. Материал стержня − сталь; предельная гибкость λпред = 100, коэффициенты a = 310 МПа, b = 1,14 МПа.
Решение. Величину коэффициента запаса устойчивости найдем,
используя условие устойчивости F ≤ FKcr по формуле K = FFcr , пред-
331
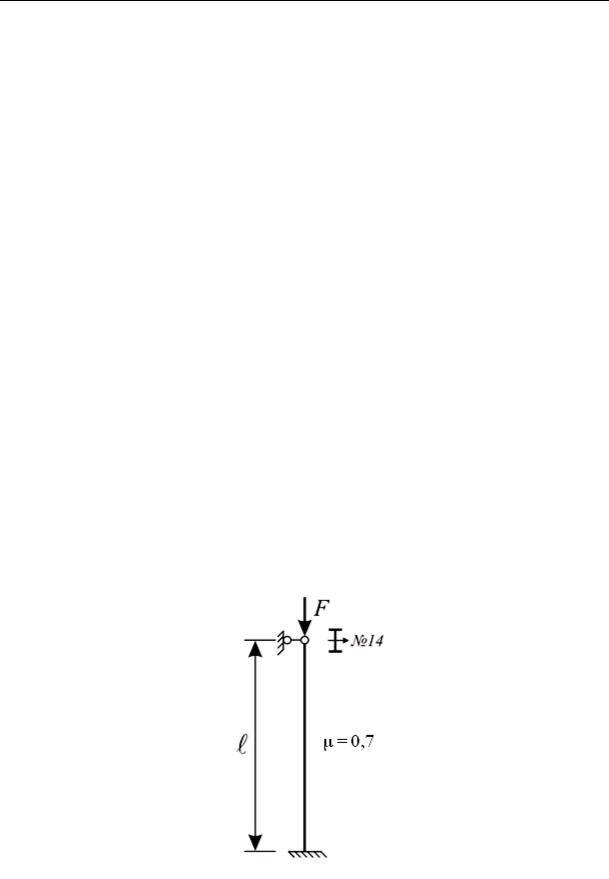
И. В. Богомаз. Механика
варительно вычислив значение критической силы Fcr, формулу для которой выберем в зависимости от гибкости стержня.
Определим геометрическиехарактеристики поперечного сечения. Из сортамента прокатной стали для двутавра № 14 имеем
A = 17,4 см2; ix = 5,73 см; iy = 1,55 см.
Очевидно, что потеря устойчивости произойдет в плоскости наименьшей жесткости, поэтому при вычислении гибкости следует
взять imin = iy. Гибкость стержня
λ = |
μ |
= |
0,7 180 |
= 81,3. |
|
i |
|
1,55 |
|
|
min |
|
|
|
Вычислимкритическуюсилу. Гибкостьстержня
λ= 81,3 < λпред = 100,
поэтому воспользуемся эмпирической формулой Ясинского:
Fcr = A(a −bλ)17, 4 10−4 (310 −1,14 81,3) 106 = 378кН.
Рис. 15.8
332
