
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ИЗ МАТЕМАТИКИ
- •1.1. Прямоугольная декартова система координат
- •1.2. Понятие об абсолютно твердом теле и его степенях свободы
- •1.3. Элементы тригонометрии
- •1.4. Векторы
- •1.5. Инерциальная система отсчета
- •2. СТАТИКА
- •2. 1. Аксиомы статики
- •2.2. Теорема о переносе вектора силы вдоль линии действия
- •3. СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ
- •3.1. Приведение к равнодействующей системы параллельных сил, направленных в одну сторону
- •3.2. Приведение к равнодействующей двух сил, направленных в разные стороны
- •3.3. Пара сил
- •3.4. Правило рычага. Момент силы относительно точки
- •3.5. Распределенные силы
- •4. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА И ОСИ
- •4.1. Момент силы
- •4.2. Приведение силы к заданному центру
- •4.3. Условия равновесия произвольной пространственной системы сил
- •4.4. Условия равновесия произвольной плоской системы сил
- •4.5. Вычисление реакций опор конструкций арочного типа
- •5. ЦЕНТР ТЯЖЕСТИ
- •5.1. Центр параллельных сил
- •5.2. Центр тяжести твердого тела
- •5.3. Центр тяжести плоского сечения
- •5.4. Центры тяжести простейших тел
- •5.5. Методы вычисления центров тяжести тел
- •6. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- •6.1. Приведение к равнодействующей силе
- •6.2. Условия равновесия системы сходящихся сил
- •6.3. Равновесие твердого тела под действием трех сил
- •7. КИНЕМАТИКА ТОЧКИ
- •7.1. Траектория, скорость, ускорение
- •7.2. Движение точки в плоскости
- •7.3. Простейшие движения твердого тела
- •8. ДИНАМИКА
- •8.1. Основные законы движения материальной точки
- •8.2. Две основные задачи динамики точки
- •8.3. Теорема об изменении кинетической энергии
- •8.4. Принцип возможных перемещений
- •8.5. Принцип Д’Аламбера. Силы инерции
- •9. ДЕФОРМИРУЕМОЕ ТВЕРДОЕ ТЕЛО
- •9.1. Общие сведения
- •9.2. Классификация нагрузок
- •9.3. Метод сечений. Виды сопротивлений бруса. Построение эпюр
- •10. ПОНЯТИЕ О НАПРЯЖЕНИИ И ДЕФОРМАЦИИ
- •10.1. Напряженное состояние в точке
- •10.2. Интегральные зависимости между внутренними силовыми факторами и напряжениями
- •10.3. Деформации и перемещения. Деформированное состояние в точке
- •11. ОСЕВОЕ РАСТЯЖЕНИЕ И СЖАТИЕ В ПРЕДЕЛАХ УПРУГОСТИ
- •11.1. Основные понятия и зависимости. Условия прочности
- •11.2. Перемещения. Эпюра перемещений. Условие жесткости
- •11.3. Расчеты на прочность и жесткость
- •12. ПЛОСКИЕ СТЕРЖНЕВЫЕ ФЕРМЫ
- •12.1. Общая характеристика и классификация ферм
- •12.2. Методы расчета плоских ферм
- •13. ИЗГИБ БРУСА
- •13.1. Поперечный изгиб
- •13.2. Расчеты на прочность при изгибе
- •13.3. Перемещения при изгибе
- •13.4. Расчет балок на жесткость
- •14. ВНЕЦЕНТРЕННОЕ СЖАТИЕ ИЛИ РАСТЯЖЕНИЕ
- •14.1. Определения. Условия прочности
- •14.2. Ядро сечения
- •15. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
- •15.1. Понятие об устойчивости
- •15.2. Продольный изгиб. Потеря устойчивости
- •15.3. Формула Эйлера для вычисления критической силы шарнирно закрепленного стержня
- •15.5. Критическое напряжение. Гибкость стержня
- •15.6. Продольный изгиб за пределом пропорциональности. Формула Ясинского
- •15.7. Диаграмма критических напряжений
- •15.8. Принципы рационального проектирования сжатых стержней
- •ОГЛАВЛЕНИЕ

14. Внецентренное сжатие или растяжение
|
|
A R |
|
|
100 10−4 120 |
106 |
|||
F ≤ |
|
|
c |
|
= |
|
|
=163,71кН, |
|
|
|
|
|
|
|||||
c |
7,33 |
|
|
|
|
7,33 |
|
||
|
|
|
|
|
|
|
|||
|
|
|
A R |
|
|
|
100 10−4 30 |
106 |
|
F ≤ |
|
t |
|
= |
|
= 85,61кН. |
|||
|
|
|
|
||||||
t |
3,504 |
|
|
3,504 |
|
||||
|
|
|
|
|
|||||
Из двух значений силы Fс и Ft в качестве несущей способности выбираем наименьшую, т. е. F ≤ 85,61 кН.
Ответ: несущая способность стойки F ≤ 85,61 кН.
14.2. Ядро сечения
Ядро сечения – часть сечения вокруг центра тяжести, при расположении внутри которой продольной нагрузки в поперечных сечениях возникают напряжения одного знака.
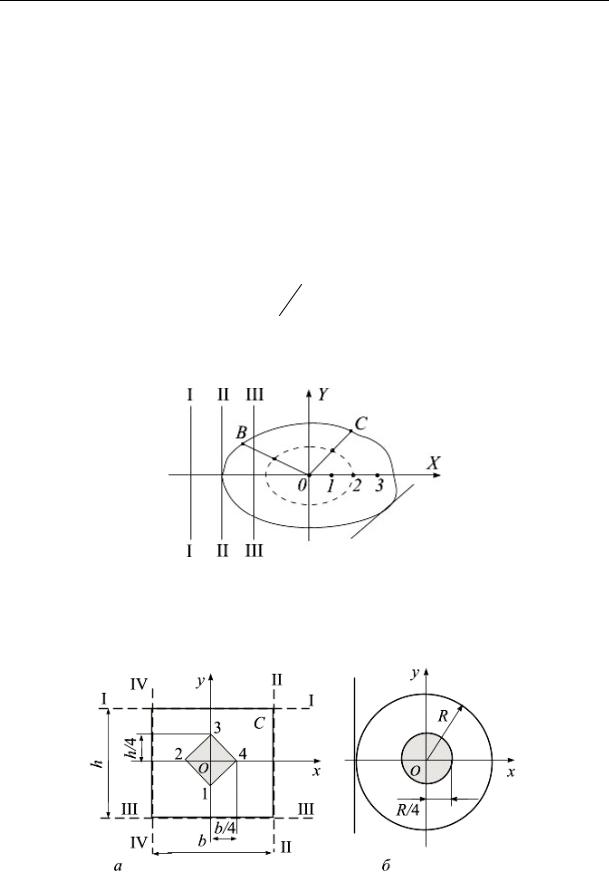
Пусть сжимающая сила F проходит точки 1, 2, 3 (рис. 14.5), тогда нейтральная линия занимает положения I–I, II–II, III–III и т. д. Наступит момент, когда нейтральная линия коснется контура сечения
изаймет, например, положение II–II, которому соответствует силовая точка 2. При этом в сечении во всех точках будут сжимающие напряжения. Если силу передвинуть за точку 2, то нейтральная линия пройдет внутри контура сечения и разделит его на 2 части: сжатую
ирастянутую. Таким образом, точка 2 является граничной точкой, за которой нельзя располагать продольную силу, если необходимо исключить возникновение в поперечном сечении растягивающих напряжений. Точно так же на прямых ОВ и ОС можно определить точки, которые обладают теми же свойствами, что и точка 2 (рис. 14.5). Соединив данные точки, получим контур ядра сечения.
Для построения ядра сечения проводят несколько нейтральных линий, касательных к контуру сечения. По чертежу находят соответ-
ствующие координаты отрезков ax и ay, отсекаемых от осей координат, и по формулам, которые следуют из (14.3), определяют координаты граничных точек ядра сечения:
|
iy2 |
|
i2 |
|
||
xF = − |
|
; |
yF = − |
x |
. |
(14.5) |
|
|
|||||
|
ax |
|
ay |
|
||
|
|
|
|
|
|
311 |
И. В. Богомаз. Механика
При проектировании колонн из материалов, имеющих низкое сопротивление растяжению (например, из чугуна, бетона, камня, кирпичной кладки), важно заранее знать размеры ядра сечения и его форму.
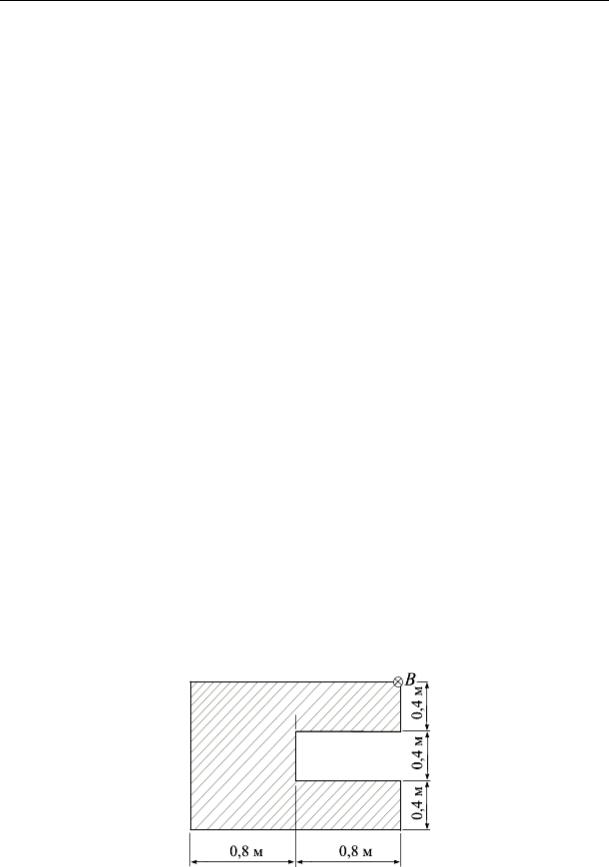
Возьмем прямоугольное сечение со сторонами b и h (рис. 14.6, а). Рассмотрим четыре положения касательной, совмещенной со сторонами прямоугольника.
Для касательной I–I отрезки, отсекаемые на осях координат, равны ax = ∞ и ay = h/2. По формулам (14.5) имеем
|
iy2 |
|
|
i |
2 |
|
2 J |
x |
|
2b h3 |
|
h |
|
xF = − |
|
= 0; |
yF = − |
x |
= − |
|
= − |
|
= − |
|
. |
||
∞ |
|
h A |
12b h2 |
6 |
|||||||||
|
|
|
h |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 14.5
Рис. 14.6
312
14. Внецентренное сжатие или растяжение
Откладываем на оси Оу отрезок (–b/6), получаем точку 1 ядра сечения. Аналогично вычисляется точка 3. Повторяя рассуждения по отношению к касательным II–II и IV–IV, вычисляем для точек 2 и 4 координаты yF = 0; xF = ±b/6. Соединив вычисленные координаты точек прямыми линиями, получим ядро сечения в виде ромба (рис. 14.6, а).
Для сечения в виде круга радиусом R ядро сечения очерчено по окружности радиусом R/4 (рис. 14.6, б). Ввиду того, что круг симметричен относительно центра, достаточно рассмотреть одно положение касательной: ax = –R. Тогда
xF = r = |
J y |
|
πR4 |
R |
|
|
|
= |
|
= |
|
. |
|
A R |
|
4 |
||||
|
|
4 πR2 R |
|
|||
Для сечения, имеющего форму многоугольника, ядро сечения также будет многоугольником.
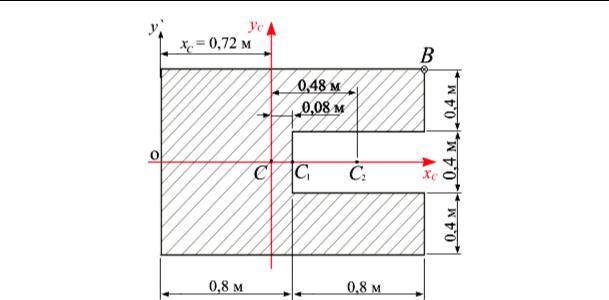
Пример 14.2. Колонна заданного поперечного сечения (рис. 14.7) сжата силой, приложенной в точке В сечения. Найти положение нейтральной линии и построить ядро сечения.
Решение. Вычислим геометрические характеристики поперечного сечения, используя метод отрицательных площадей. Имеем
A1 =1,6 1, 2 =1,92 м2 , A2 = −0,8 0, 4 = −0,32м2 ,
А= ∑Ai = А1 + А2 =1,92 −0,32 =1,6м2 .
Рис.14.7
313
И. В. Богомаз. Механика
Рис. 14.8
Вычислим координаты центра тяжести C{xc, yc} осей Oxy' заданного поперечного сечения (рис. 14.8):
y |
= 0, х |
= |
А1 хс1 + А2 хс2 |
= 1,92 0,8 −0,32 1, 2 = |
|
||||
c |
с |
A |
1,6 |
|
|
|
|
||
относительно
0,72м.
Проводим через точку C{xc, yc} главные оси Cxcyc.
Осевые моменты инерции сечения относительно главных осей Cxcyc равны:
|
|
|
|
|
|
|
Jx = 1,6 1, 23 |
− 0,8 0, 43 |
= 0, 226м4 , |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
12 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
1, 2 1,63 |
+ 0,08 |
2 |
|
|
0, 4 0,83 |
+ 0, 48 |
2 |
0,32 |
|
= 0,331м |
4 |
. |
||||||||
J y = |
|
12 |
|
|
|
1,92 |
− |
12 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Квадраты радиусов инерции: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
ix2 |
= |
J |
x |
= |
0, 226 |
= 0,141м2 |
, iу2 = |
J |
у |
= |
0,331 |
= 0, 206м2 . |
|
|
||||||
|
A |
1,6 |
|
A |
1,6 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
314
14. Внецентренное сжатие или растяжение
Вычислим координаты отрезков, отсекаемые нейтральной линией на осях координат Cxcyc (координаты полюса В: xF = 0,88 см, yF = 0,6 см):
|
iy2 |
|
0, |
206 |
|
i2 |
0,141 |
|
|
ах = − |
|
= − |
|
|
= −0,234м, ау = − |
х |
= − |
|
= −0,235м. |
xF |
0,88 |
|
0,6 |
||||||
|
|
|
уF |
|
|||||
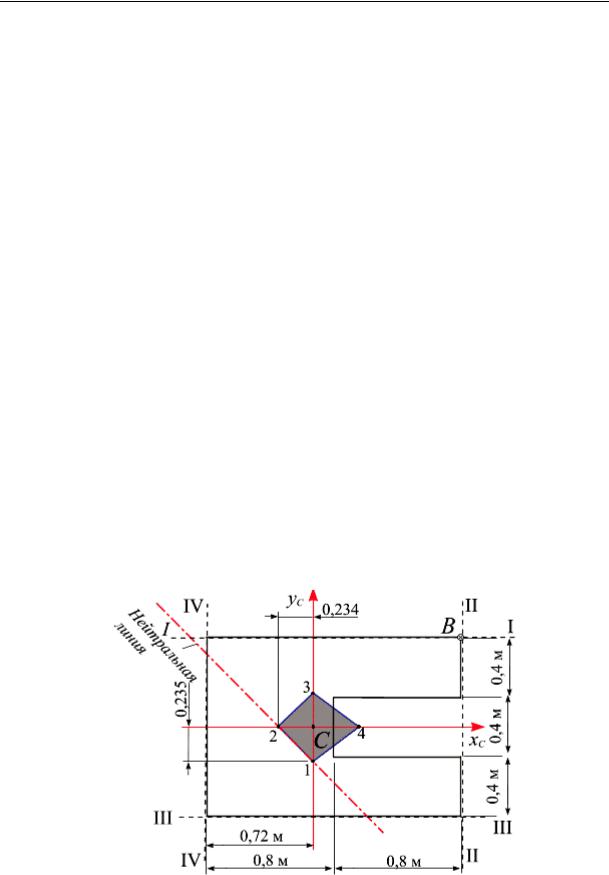
Построим нейтральную линию, отложив вычисленные отрезки на соответствующих координатных осях с учетом знака (рис. 14.9).
Для построения ядра сечения проведем четыре линии, касательные к контуру сечения (рис. 14.9) и вычислим координаты граничных точек ядра сечения по формуле (14.5).
Для касательной I–I длины отрезков, отсекаемых на осях координат, равны ах = ∞, ау = 0,6 м, тогда координаты точки 1 ядра сечения:
|
iy2 |
|
iy2 |
|
i2 |
0,141 |
|
|
xF = − |
|
= − |
|
= 0; yF = − |
x |
= − |
|
= −0,235м. |
ax |
∞ |
|
0,6 |
|||||
|
|
|
ay |
|
||||
Для касательной II–II:
ах = 0,88 м, ау = ∞.
Рис. 14.9
315

И. В. Богомаз. Механика
Координаты точки 2:
|
0, 206 |
|
|
i2 |
|
|
xF = − |
|
= −0, 234(м), |
yF = − |
x |
= 0. |
|
0,88 |
∞ |
|||||
|
|
|
|
Для касательной III–III:
ах = ∞, ау = – 0,6 м.
Координаты точки 3:
xF = − |
iy2 |
= 0, yF = − |
0,141 |
= 0, 235м. |
|
∞ |
−0,6 |
||||
|
|
|
Для касательной IV–IV:
ах = – 0,72 м, ау = ∞.
Координаты точки 4:
|
0, 206 |
|
|
i2 |
|
|
xF = − |
|
= 0, 286м, |
yF = − |
x |
= 0. |
|
−0,72 |
∞ |
|||||
|
|
|
|
Соединив точки 1–2–3–4 прямыми линиями, получим ядро сечения (рис. 14.9).
316
