11. Осевое растяжение и сжатие в пределах упругости
Тогда абсолютное удлинение участка |
Aстержня длиной A при |
|||
A = const и E = const будет равно |
|
|
|
|
A = |
NA |
, |
(11.9) |
|
EA |
||||
|
|
|
||
где EA – жесткость стержня при растяжении (сжатии).
Формула (11.9) выражает закон Гука для абсолютной продольной деформации, ее называют формулой жесткости при растяжении и сжатии.
Для бруса, имеющего несколько участков,
A = ∑ Ai . |
(11.10) |
Удлинение, связанное с температурным воздействием, |
|
A°t = A α t , |
(11.11) |
где α – коэффициент температурного расширения материала; |
t – из- |
менение температуры. |
|
При растяжении (сжатии) поперечные сечения стержня перемещаются в продольном направлении; перемещения поперечных сечений – это следствие деформации. При осевом нагружении бруса длиной A и с постоянной площадью поперечного сечения A перемещение
δ(zi) любого i-го сечения |
|
|
|
|
|
|
|
|
|
|
δ(z ) = zi |
N (z)dz |
= |
|
1 zi |
N (z)dz , |
(11.12) |
||||
|
|
|
|
|
||||||
|
|
EA ∫ |
||||||||
i |
∫ |
EA |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|||
а при одинаковой по длине силе N вычисляется по формуле |
|
|||||||||
|
|
δ(z ) = |
N zi |
. |
|
(11.12’) |
||||
|
|
|
|
|||||||
|
|
i |
EA |
|
|
|||||
|
|
|
|
|
|
|
||||
Эпюру перемещений δ(z) начинают строить от защемленного конца бруса, вычисляя перемещения в характерных сечениях (как правило, это границы участков).
241
11. Осевое растяжение и сжатие в пределах упругости
Зависимость (11.17) можно использовать для контроля эпюры δz: На участке, где Nz = const, перемещение δz изменяется по линей-
ному закону.
1.На участке, где N(z) изменяется по линейному закону, δz изменяется как квадратичная функция.
2.Если на участке N(z) > 0, то δz возрастает; если N(z) < 0, то δz убывает.
3.В сечении, где N(zO) = 0 (эпюра пересекает базисную линию), перемещение δz имеет экстремальное значение.
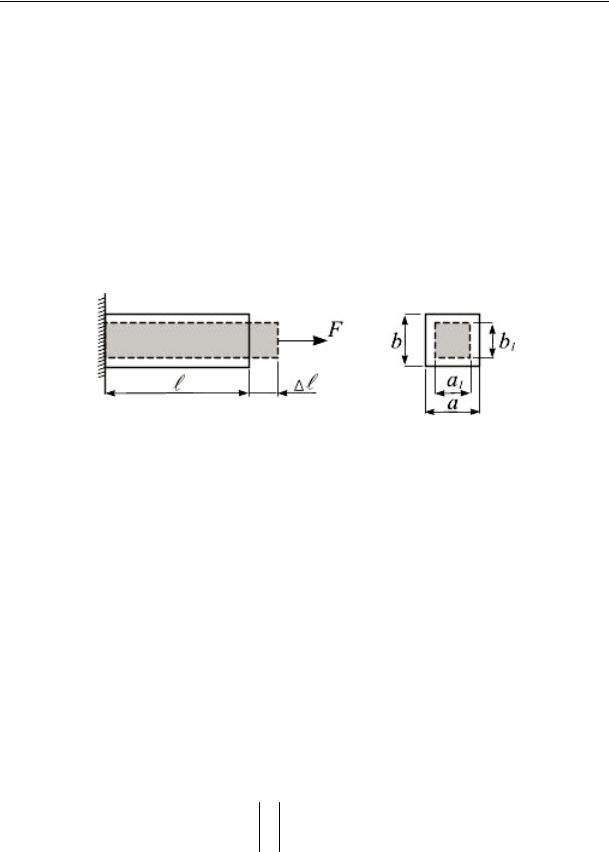
Растяжение (сжатие) сопровождается изменением поперечных размеров (рис. 11.9).
Рис. 11.9
Абсолютная поперечная деформация определяется как разность размеров после деформации и до нее:
a = a1 – a; |
b = b1 – b. |
Относительная поперечная деформация для изотропных материалов по всем направлениям одинакова.
ε′ = aa = bb .
Между поперечной и продольной относительными деформациями, которые всегда противоположны по знаку, в пределах закона Гука существует постоянное отношение
ν = |
ε′ |
′ |
|
|
|
ε или ε |
= −νε, |
(11.18) |
|||
|
где v – коэффициент поперечной деформации (коэффициент Пуассона) – безразмерная величина, упругая постоянная материала, опреде-
243