7. Кинематика точки
V = lim |
(t) |
= |
dS(t) |
. |
t |
|
|||
t→0 |
|
dt |
||
Исаак Ньютон и Готфрид Вильгельм Лейбниц заложили основы новой области математики – дифференциального и интегрального исчисления.
7.2. Движение точки в плоскости
Координатный способ задания движения точки. Уравнения движения точки в декартовых координатах Оху имеют вид
x = x(t), y = y(t). |
(7.3) |
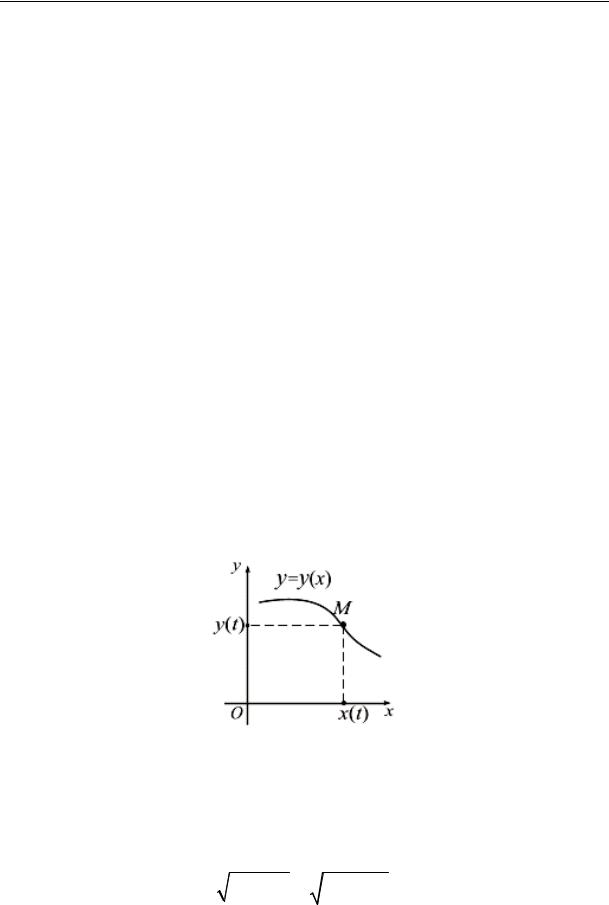
Уравнения (7.3) являются также уравнениями траектории точки, заданными параметрически. Уравнение траектории в системе координат Oxy будет иметь вид функции y = y(x) (рис. 7.4). Для получения этой зависимости следует из уравнений (7.3) исключить параметр t .
Уравнение траектории в явном виде будет иметь вид функции y = y(x).
Скорость и ускорение точки по модулю и направлению вычисляются по формулам
|
|
|
|
|
= x2 + y2 = V 2 |
+V 2 |
, cos α = |
x |
; |
V = |
V |
|
|||||||
|
|
|
|||||||
|
|
|
|
|
x |
y |
V |
|
|
|
|
|
|
|
|
|
|
||
137
И. В. Богомаз. Механика
|
a = |
|
a |
|
= x2 + y2 = |
a2 |
+ a2 |
, cos α = |
x |
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
x |
y |
1 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 7.1. Движение точки M по плоскости Оху задано урав- |
|||||||||||
нениями движения |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x = 2sin (2t ), |
y = 4cos(2t ). |
|
|
(а) |
|||
Построить траекторию движущейся точки, вычислить скорость и ускорение точки в моменты времени t1 = π4 и t2 = 58π .
Решение. Для построения траектории движущейся точки в де-
картовой системе координат определим область, в которой движется точка, т. е. область значений x(t) и y(t).11 Функции sin(2t) и cos(2t) ог-
раничены, т. е. |
|
sin (2t) |
|
≤1, |
|
cos(2t) |
|
≤1, получаем |
|
|
|
|
|||||
|
|
–2 ≤ x ≤ 2; |
|
–4 ≤ y ≤ 4. |
||||
Выделяем область, ограниченную полученными неравенствами, за эту область точка при движении не выходит (рис. 7.4). Исключим параметр t из уравнений движения (a). Для этого первое уравнение делим на второе, второе – на четвертое, возводим их в квадрат и складываем между собой:
|
x 2 |
= sin |
2 |
(2 t ) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 |
= cos |
2 |
|
(2 t ); |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
y |
2 |
= sin |
2 |
(2t )+ cos |
2 |
(2t ). |
|||||
|
|
|
|
|
+ |
|
|
|
|
|
|||||
2 |
|
|
4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учитывая, что sin2 (2t )+cos2 (2t )=1, получим
x |
2 |
|
y 2 |
|
||||
|
|
|
+ |
|
|
=1. |
(б) |
|
2 |
4 |
|||||||
|
|
|
|
|
|
|||
11 В теории функций одной переменной эта процедура определяет область задания (существования) функций x(t) и y(t). Область определения функций в классической кинематике всегда определена: t ≥ 0.
138
7. Кинематика точки
Рис. 7.5
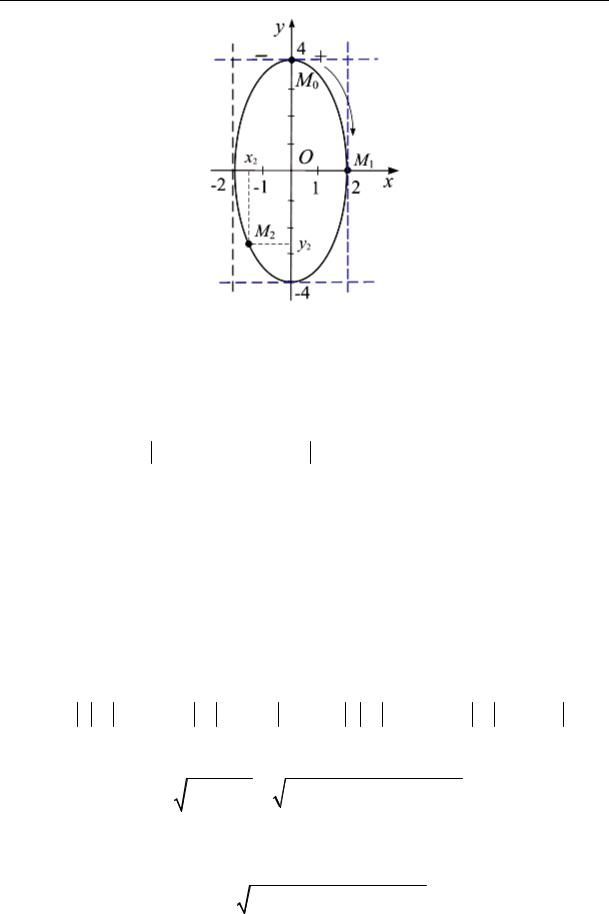
Траекторией движущейся точки является эллипс (рис. 7.5). Подставляя в (а) значение t = 0, находим
x t =0 = 2sin (0) = 0 ; y t =0 = 4cos(0) = 4 см.
Точка в начальный момент времени занимает положение M0 (0, 4). Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией x = 2sin(2t) и убывающей функцией y = 4cos(2t), поэтому при увеличении t координата х возрастает, а у убывает, следовательно, точка движется по эллипсу по часовой стрелке.
Вычислим модуль и направление вектора скорости точки М. Имеем
Vx = x = 2 2cos 2t = 4cos 2t , Vy = y = −4 2sin 2t = −8sin 2t ,
|
|
|
|
|
(в) |
V = V 2 |
+V 2 |
= |
(4cos 2t)2 +(8sin 2t)2 , |
||
x |
|
y |
|
|
|
cos α = |
|
|
4cos 2t |
. |
|
|
|
|
|||
(4cos 2t)2 +(8sin 2t)2
139
И. В. Богомаз. Механика
Вычислим модуль и направление вектора ускорения точки М. Имеем
ax = |
|
x |
|
=Vx = |
|
−4 2sin 2t |
|
= |
|
|
|
−8sin 2t |
|
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
ay = |
|
y |
|
=Vy = |
|
−8 2cos 2t |
|
|
= |
|
−16cos 2t |
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
a = (8sin 2t) +(16cos 2t), cos(a, x) = |
|
−8sin 2t |
. (г) |
|||||||||||||||||||||
|
(8sin 2t) +(16cos 2t) |
|||||||||||||||||||||||
При t1 = π4 из (а) получаем, что точка М имеет координаты х = 2,
у = 0, т. е. занимает положение (рис. 7.5) М1. Подставляя в (в) и (г)
время t1 = π4 , получим
V |
|
|
4cos 2t |
|
|
|
4cos(2 π) |
|
= 0, V |
= |
|
−8sin 2t |
|
π = |
|
−8sin (2 π) |
|
= |
|
−8 |
|
, |
|||||||
= |
|
|
|
π = |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
1x |
|
|
|
|
|
t=4 |
|
|
4 |
|
1y |
|
|
|
|
|
|
t=4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
V = |
V |
2 |
+V 2 |
|
= 8 м/с, |
|
|
|
, x) = 0 |
= 0; |
α = −90°; |
|||||||||||||||||
|
|
|
cos α = cos (V |
||||||||||||||||||||||||||
|
1 |
1x |
1y |
|
1 |
1 |
8 |
|
|
|
1 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a1x = −8sin 2t t=π4 = −8sin (2 π4) = −8 ,
a1y = −16cos 2t t=π4 = −16cos(2 π4) = 0,
a |
= a2 |
+ a2 |
=8 м/с, |
cosβ = cos(a, x) = |
a1x |
= −8 = −1, |
β =180°. |
||
|
|||||||||
1 |
1x |
1y |
|
1 |
|
|
a1 |
8 |
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
точки М1 на |
|||||
|
Откладываем значения скорости V1 и ускорения a1 |
||||||||
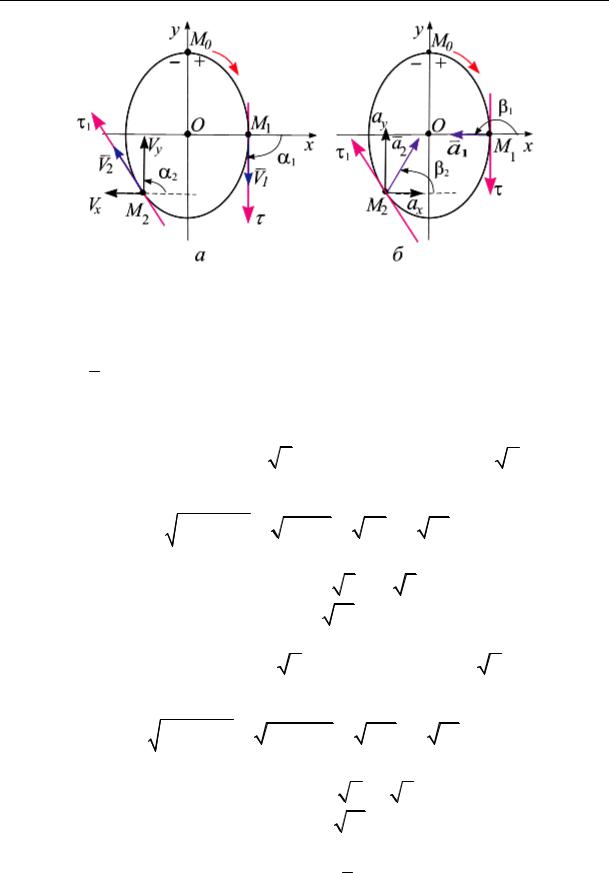
траектории (рис. 7.6, а, б).
При t2 = 58π из (а) получаем координаты точки М2:
x2 = − 2 = −1,41м, y2 = −2 2 = −2,83м.
140
7. Кинематика точки
Рис. 7.6
Вычислим, используя (в) и (г), модуль и направление векторов скорости V2 и ускорения a2 .
Имеем
V2x = |
|
4cos 2t |
|
t= |
5π = |
−2 2 |
|
|
, V2 y = |
|
|
−8sin 2t |
|
t= |
5π = 4 2, |
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
V = V |
2 |
+V 2 |
|
= 8 +32 = 40 = 2 10 м/с; |
|||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
2x |
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
, x) = cos α |
|
= |
V2x |
= |
−2 |
2 = − |
5 |
, |
|
α |
|
|
=134°. |
||||||||||||||||||||||||
cos(V |
2 |
|
2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
2 10 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a2x |
= |
|
−8sin 2t |
|
t= |
5π = 4 |
2 , a2 y = |
|
−16cos 2t |
|
= 8 2 , |
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 м/с2; |
|||||
a |
= |
|
|
|
a2 |
+ a |
2 |
= |
32 +128 = |
|
|
|
160 = 4 |
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
2x |
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(a |
2 |
, x) |
= cosβ |
2 |
= |
a2x |
|
= |
4 |
2 |
|
|
|
|
= |
|
5 |
, β |
2 |
= 64°. |
|||||||||||||||||||
a2 |
|
|
|
|
|
|
|
5 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
10 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Откладываем значения скорости V2 и ускорения a2 точки М2 на траектории (рис. 7.6, а, б).
141
И. В. Богомаз. Механика
Рис. 7.7
Вектор скорости точки совпадает по направлению с касательной к траектории в точках М1 и М2, а вектор ускорения в точках М1 и М2 направлен вовнутрь вогнутости траектории (к центру О).
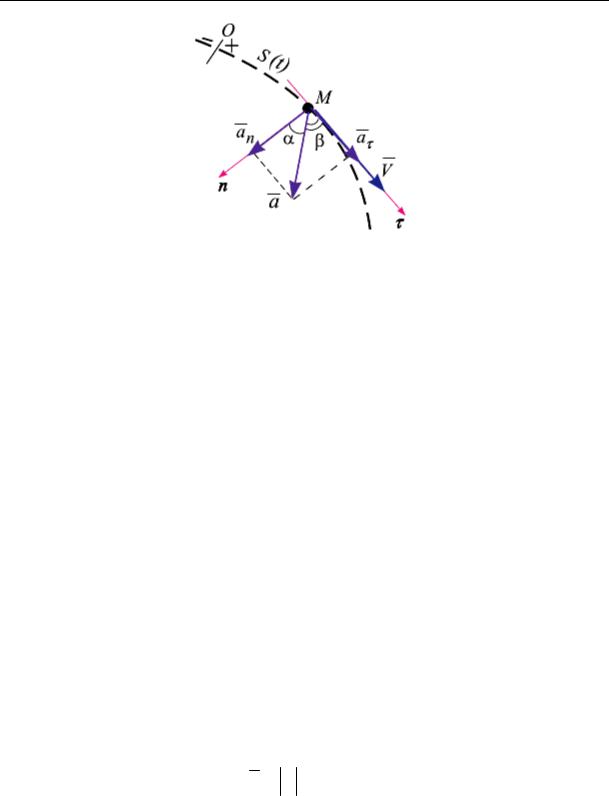
Естественный способ задания движения точки. При естест-
венном способе задания движения точки задается:
•траектория движения точки;
•начало и направление увеличения дуговой координаты S;
•уравнение движения точки по траектории как функция времени: S = S(t), где S – дуговая координата, отчитываемая от начала движения (рис. 7.7).
Примером естественного способа задания движения является движение поезда: траектория и направление движения определены рельсами, а уравнение движения задано таблицей – расписанием движения поезда.
Движение точки рассматривается в координатах Mτn. Единичный вектор τ направлен по направлению вектора скорости, единичный вектор n перпендикулярен вектору τ, направлен по главной нормали кривой в сторону ее вогнутости (рис. 7.7).
Скорость точки M направлена по касательной и равна
V = S τ =Vτ τ.
Ускорение a точки M при естественном способе задания движения раскладывается на два: на касательное ускорение
aτ = S τ =Vτ τ
142
7. Кинематика точки
и нормальное ускорение
an = Sρ2 n = Vρτ2 n
a = aτ + an .
Касательное ускорение aτ характеризует изменение величины скорости, нормальное an – изменение направления вектора скорости.
Естественный способ задания движения – S(t) + траектория.
|
|
|
|
|
|
|
|
|
|
|
S |
τ =Vτ τ. |
|||||||
|
|
|
|
|
|
|
V |
= |
|||||||||||
|
|
|
|
|
|
|
|
|
a = aτ + an , |
||||||||||
где |
касательное ускорение |
|
aτ |
= S =Vτ ; нормальное ускорение |
|||||||||||||||
|
|
S 2 |
|
V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
= |
|
= |
|
τ |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
a = |
a2 |
+ a2 |
, tg α = |
|
|
aτ |
|
|
. |
||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
τ |
|
n |
|
|
|
an |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Движение точки в плоскости по окружности. Введем радиус- |
|||||||||||||||||
вектор r = r (t) . Совместим начало радиус-вектора с центром окружно-
сти О, полярную ось направим по радиусу (рис. 7.8, а). Тогда при движении точки будет меняться только угол между радиус-вектором и осью , модуль радиус-вектора остается постоянным. Следовательно, описывать движение точки можно одним параметром – углом φ.
Зададим движение точки естественным способом. Совместим оси естественного трехгранника с точкой М – ось Mn совпадает с радиусом и проходит через центр окружности, ось Mτ направлена в сторону движения точки и перпендикулярна радиусу.
Известно, что длина дуги, радиус окружности и угол ϕ связаны
между собой:
S(t) = r ϕ(t).
Введем обозначения: ϕ = ω0 – круговая скорость, ϕ = ε0 – круговое ускорение.
143