6. Система сходящихся сил
6. СИСТЕМА СХОДЯЩИХСЯ СИЛ
6.1. Приведение к равнодействующей силе
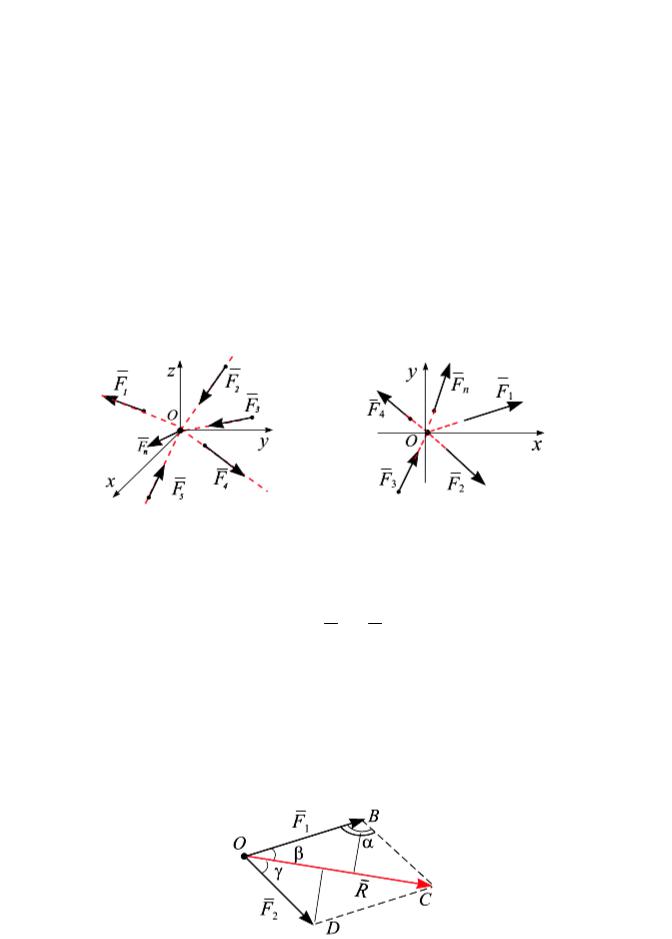
Системой сходящихся сил, расположенных в одной плоскости, называется система сил, линии действия которых пересекаются в одной точке. Сходящиеся системы сил могут быть пространственными (рис. 6.1, а) и плоскими, т. е. расположенными в одной плоскости
(рис. 6.1, б).
а |
б |
Рис. 6.1
На тело действует две силы F1 и F 2 , приложенные в одной точке О и образующие между собой угол β + γ (рис. 6.2).
Две силы, приложенные в одной точке и направленные под углом друг к другу, эквивалентны одной силе (равнодействующей), приложенной в той же точке, равной по модулю и направлению диагонали параллелограмма, стороны которого изображают величины и направления обеих заданных сил.
Рис. 6.2
119
И. В. Богомаз. Механика
Равнодействующая R этих двух сил равна геометрической сумме этих сил (рис. 6. 2), т. е.
R = F 1+F2 .
Из рис. 6.2 видно, что сумма проекций двух сил F1 и F 2 на линию действия равнодействующей ОС равна модулю равнодействующей
F1 cosβ + F2 cos γ = R.
Параллелограмм, стороны которого отображают величины и направления заданных сил, состоит из двух равных треугольников (рис. 6.3). Сторона ВС параллелограмма равна модулю вектора си-
лы F 2 . Если рассмотреть ∆OBC, то равнодействующую силу R можно получить как замыкающую этот треугольник. Этот треугольник принято называть силовым.
Направление равнодействующей R (углы β и γ) вычисляется по теореме синусов
sinRα = sinF1γ = sinF2β.
Вычислим модуль равнодействующей, используя теорему косинусов:
R = F 2 |
+ F 2 |
−2F F cos α = |
F 2 |
+ +F 2 |
+ 2F F cos(β+ γ). |
||
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
Здесь α > 90°, β+ γ < 90°.
Рис. 6.3
120
6. Система сходящихся сил
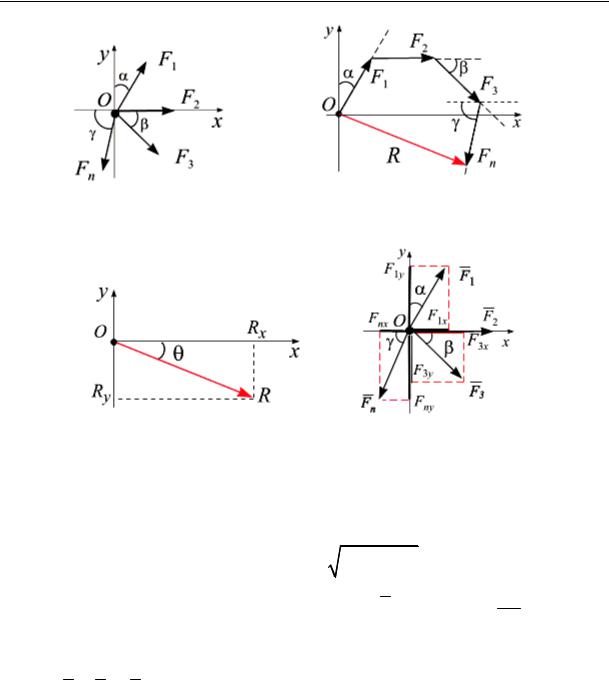
Рассмотрим общий случай системы сходящихся сил (рис. 6.4, а). Так как силы, действующие на твердое тело, являются скользящими
векторами, то можно считать, что силы F1, F 2 … F n этой системы сходящихся сил все приложены в точке О.
Равнодействующая R системы сходящихся сил равна геометрической сумме этих сил:
R = ∑Fi = F1 + F2 +…+ Fn.
Геометрическое вычисление равнодействующей. Равнодейст-
вующая R системы сходящихся сил (рис. 6.4, а) может быть получена построением силового многоугольника из заданных сил. Совмещаем начало декартовой системы координат с точкой пересечения линий действия сил, т. е. с точкой О.
Из точки О проводим прямую, параллельную линии действия силы F1, и откладываем в масштабе модуль этой силы (рис. 6.4, б).
Далее от конца вектора силы F1 проводим прямую, параллельную линии действия второй силы, и откладываем вдоль полученной прямой модуль второй силы и т. д.
В силовом многоугольнике конец одной из сил служит началом
другой. Равнодействующая R в силовом многоугольнике соединяет начало координат (точка О) с концом вектора последней силы. Силы в силовом многоугольнике можно изображать в любой последова-
тельности. Измеряем длину полученного вектора R и с учетом мас-
штаба получаем модуль равнодействующей R . Измеряя угол θ, по-
лучаем направление вектора R (рис. 6.4, в).
Аналитическое вычисление равнодействующей. Для аналити-
ческого вычисления равнодействующей R системы сил следует спроецировать заданные силы на оси Ox и Oy, так как проекция замыкающей любого многоугольника на ось равна алгебраической сумме проекций составляющих его сторон на ту же ось (рис. 6.4, г). Проецируя заданные векторы сил на прямоугольную систему координат, получим
Rx = ∑Fix =F1 sin α + F2 + F3 cosβ− Fn cos γ,
Ry = ∑Fiy =F1 cosα − F3 sinβ− Fn sin γ.
121
И. В. Богомаз. Механика
а |
б |
в |
г |
Рис. 6.4
Модуль равнодействующей R = Rx |
2 + Ry |
2 . |
Направление равнодействующей cos (R, x )≡ cos θ = RRx .
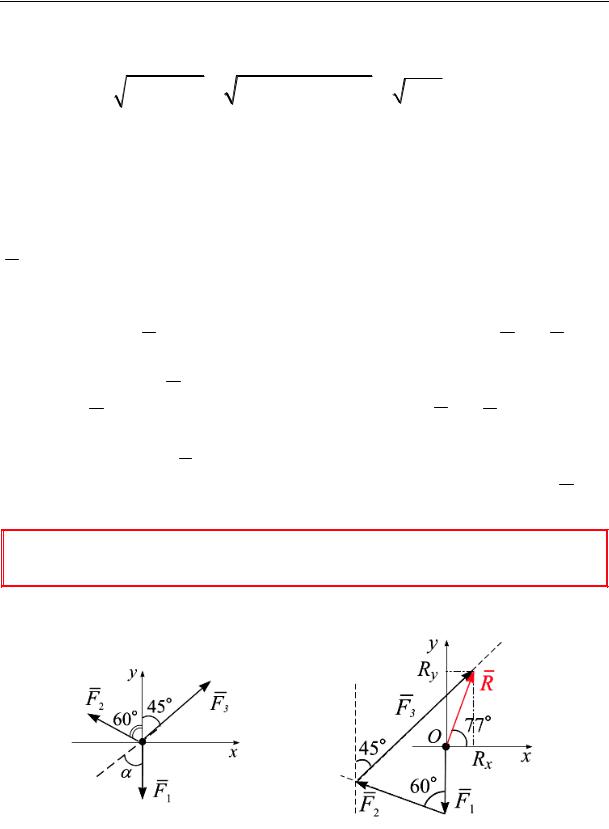
Пример 6.1. Вычислить равнодействующую системы сходящихся силF1 , F2 , F3 , приложенных в точку О (рис. 6.5, а), аналитически
и геометрически, если F1 = 6 кН, F2 = 8 кН, F3 = 10 кН.
Решение. Совместим прямоугольную систему координат с точкой О, точкой пересечения линий действия заданных сил.
Аналитическое вычисление равнодействующей. Проецируем заданные векторы сил на прямоугольную систему координат, получим
(рис. 6.5, а)
Rx = ∑Fix = −F2 sin 60°+ F3 sin 45° = −8 0,87 +12 0,707 =1,52 кН;
122
6. Система сходящихся сил
Ry = ∑Fiy =− F1 + F2 cos 60°+ F3 cos 45° = −6 +8 0,5 +12 0,707 = 6, 48кН;
R = R |
2 + R 2 |
= (1,52)2 +(6,48)2 = 44,3 = 6,65 кН, |
||||||||
x |
|
|
y |
|
|
|
|
|
|
|
cos ( |
|
, x ) |
= cosθ = |
Rx |
= |
1,52 |
= 0,23 |
θ = 77 . |
||
R |
||||||||||
|
6,65 |
|||||||||
|
|
|
|
|
R |
|
|
|||
Геометрическое вычисление равнодействующей. Из точки О (рис. 6.5, б) проводим прямую, параллельную линии действия силы
F1, и откладываем отрезок вдоль этой линии, равный модулю этой силы.
Далее через его конец проводим прямую, параллельную линии
действия силы F 2 (угол между линиями действия сил F1 и F 2 равен 60°), и откладываем на ней отрезок, равный модулю силы F2; че-
рез конец вектора F 2 проводим прямую, параллельную линии действия силы F 3 (угол между линиями действия сил F 2 и F 3 равен 75°), и откладываем на ней отрезок, равный модулю силы F3 (рис. 6.5, б). Равнодействующая R в силовом многоугольнике соединяет начало координат О (точка приложения первой силы) с концом вектора F 3 .
Равнодействующая является замыкающей векторного многоугольника, сторонами которого являются слагаемые силы.
а |
б |
Рис. 6.5
123