
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ИЗ МАТЕМАТИКИ
- •1.1. Прямоугольная декартова система координат
- •1.2. Понятие об абсолютно твердом теле и его степенях свободы
- •1.3. Элементы тригонометрии
- •1.4. Векторы
- •1.5. Инерциальная система отсчета
- •2. СТАТИКА
- •2. 1. Аксиомы статики
- •2.2. Теорема о переносе вектора силы вдоль линии действия
- •3. СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ
- •3.1. Приведение к равнодействующей системы параллельных сил, направленных в одну сторону
- •3.2. Приведение к равнодействующей двух сил, направленных в разные стороны
- •3.3. Пара сил
- •3.4. Правило рычага. Момент силы относительно точки
- •3.5. Распределенные силы
- •4. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА И ОСИ
- •4.1. Момент силы
- •4.2. Приведение силы к заданному центру
- •4.3. Условия равновесия произвольной пространственной системы сил
- •4.4. Условия равновесия произвольной плоской системы сил
- •4.5. Вычисление реакций опор конструкций арочного типа
- •5. ЦЕНТР ТЯЖЕСТИ
- •5.1. Центр параллельных сил
- •5.2. Центр тяжести твердого тела
- •5.3. Центр тяжести плоского сечения
- •5.4. Центры тяжести простейших тел
- •5.5. Методы вычисления центров тяжести тел
- •6. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- •6.1. Приведение к равнодействующей силе
- •6.2. Условия равновесия системы сходящихся сил
- •6.3. Равновесие твердого тела под действием трех сил
- •7. КИНЕМАТИКА ТОЧКИ
- •7.1. Траектория, скорость, ускорение
- •7.2. Движение точки в плоскости
- •7.3. Простейшие движения твердого тела
- •8. ДИНАМИКА
- •8.1. Основные законы движения материальной точки
- •8.2. Две основные задачи динамики точки
- •8.3. Теорема об изменении кинетической энергии
- •8.4. Принцип возможных перемещений
- •8.5. Принцип Д’Аламбера. Силы инерции
- •9. ДЕФОРМИРУЕМОЕ ТВЕРДОЕ ТЕЛО
- •9.1. Общие сведения
- •9.2. Классификация нагрузок
- •9.3. Метод сечений. Виды сопротивлений бруса. Построение эпюр
- •10. ПОНЯТИЕ О НАПРЯЖЕНИИ И ДЕФОРМАЦИИ
- •10.1. Напряженное состояние в точке
- •10.2. Интегральные зависимости между внутренними силовыми факторами и напряжениями
- •10.3. Деформации и перемещения. Деформированное состояние в точке
- •11. ОСЕВОЕ РАСТЯЖЕНИЕ И СЖАТИЕ В ПРЕДЕЛАХ УПРУГОСТИ
- •11.1. Основные понятия и зависимости. Условия прочности
- •11.2. Перемещения. Эпюра перемещений. Условие жесткости
- •11.3. Расчеты на прочность и жесткость
- •12. ПЛОСКИЕ СТЕРЖНЕВЫЕ ФЕРМЫ
- •12.1. Общая характеристика и классификация ферм
- •12.2. Методы расчета плоских ферм
- •13. ИЗГИБ БРУСА
- •13.1. Поперечный изгиб
- •13.2. Расчеты на прочность при изгибе
- •13.3. Перемещения при изгибе
- •13.4. Расчет балок на жесткость
- •14. ВНЕЦЕНТРЕННОЕ СЖАТИЕ ИЛИ РАСТЯЖЕНИЕ
- •14.1. Определения. Условия прочности
- •14.2. Ядро сечения
- •15. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
- •15.1. Понятие об устойчивости
- •15.2. Продольный изгиб. Потеря устойчивости
- •15.3. Формула Эйлера для вычисления критической силы шарнирно закрепленного стержня
- •15.5. Критическое напряжение. Гибкость стержня
- •15.6. Продольный изгиб за пределом пропорциональности. Формула Ясинского
- •15.7. Диаграмма критических напряжений
- •15.8. Принципы рационального проектирования сжатых стержней
- •ОГЛАВЛЕНИЕ
И. В. Богомаз. Механика
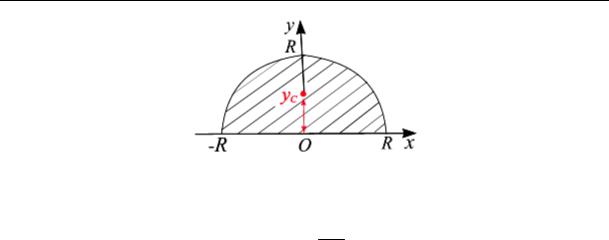
Рис. 5.7
Центр тяжести полукруга yC = 43Rπ .
5.5. Методы вычисления центров тяжести тел
Метод разбиения на части. Некоторые тела сложной формы можно разбить на части, положение центра тяжести которых известно. В таких случаях центр тяжести составного тела вычисляют по формуле
|
n |
|
n |
|
|
∑Ai xi |
|
∑Ai yi |
|
x = |
i=1 |
, y = |
i=1 |
. |
|
|
|||
C |
A |
C |
A |
|
|
|
|
Здесь A = ∑Ai – площадь сечения; xi, yi – центр тяжести i-го сечения; Ai – площадь i-го сечения.
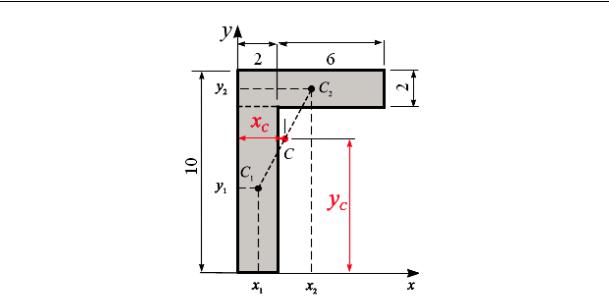
Пример 5.1. Вычислить координаты центра тяжести однородного сечения, составленного из двух прямоугольников (рис. 5.8). Размеры прямоугольников показаны на рис. 5.8 в см.
Решение. Разбиваем сечение на два прямоугольника (линии разреза показаны пунктиром) и проводим оси координат (рис. 5.8).
Вычислим координаты центров тяжести и площадь каждого из прямоугольников:
x =1cм, |
|
x = 4 см, |
||
|
1 |
|
|
2 |
y1 = 4 см, |
|
y2 = 9 см, |
||
|
А = 2 8 =16cм2 |
; |
|
А =8 2 =16см2. |
|
1 |
|
|
2 |
112
5. Центр тяжести
Рис. 5.8
Площадь всего сечения
|
|
|
3 |
|
|
|
|
|
|
|
А= ∑Аk = А1 + А2 =16 +16 = 32 см2. |
||||
Тогда |
|
|
|
k=1 |
|
|
|
|
|
|
x1 A1 + x2 A2 |
= 1 16 + 4 16 = 80 = 2,5см; |
|||
|
x |
= |
|||||
|
|
||||||
|
С |
|
A |
32 |
32 |
||
|
|
|
|
||||
y |
= |
y1 A1 + y2 A2 |
= 4 16 +9 16 = 64 +144 = 6,5см. |
||||
|
|||||||
С |
|
|
|
A |
32 |
32 |
|
|
|
|
|
||||
Положение центра тяжести совпадает с точкой С {2,5; 6,5}
(рис. 5.7).
Метод отрицательных площадей. В данном методе вырезан-
ные сечения заменяют отрицательными площадями. Проиллюстрируем этот метод на примере сечения.
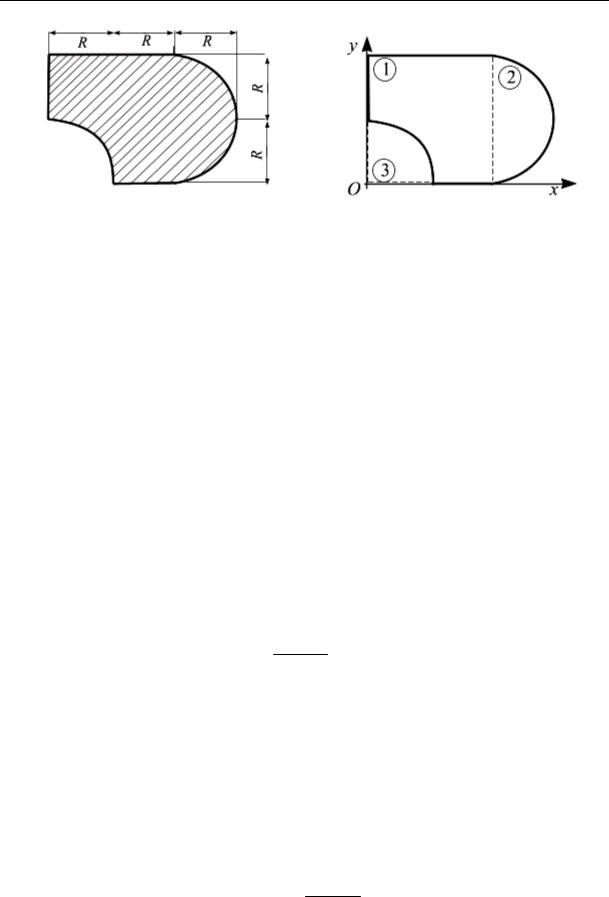
Пример 5.2. Задано сечение (рис. 5.9, а). Дано: R = 6 см. Вычислить центр тяжести сечения.
Решение. Разобьем сечение на простые фигуры: дополним квадрат – сечение 1, полукруг – сечение 2 и четверть круга – сечение 3 (рис. 5.9, б). За вспомогательную систему координат выберем стороны квадрата: Oxy. Вычислим площадь и координаты центров тяжести каждого сечения.
113
И. В. Богомаз. Механика
а |
б |
Рис. 5.9
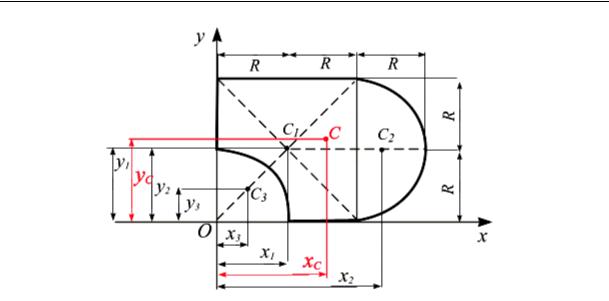
Имеем (рис. 5.10) 1. Квадрат:
A1 = 2R 2R = 4R2 = 4 62 = 4 36 =144 см2;
x1 = R = 6 см; y1 = R = 6 см.
2. Полукруг:
A2 = πR2 2 = 3,142 62 = 56,52 см2;
x2 = 2R + 43Rπ = 2 6 + 343,146 =12 + 2,55 =14,55см;
y2 = R = 6 см.
3. Четверть круга:
A3 = − πR4 2 = −3,144 62 = −28,26 см2; xC = yC = 43Rπ = 3 43.146 = 2,6 см.
114
5. Центр тяжести
Рис. 5.10
Итак, |
|
|
|
|
|
|
x |
= x1 A1 + x2 A2 + x3 A3 |
= 6 144 +14,55 56,52 −2,6 28,26 = |
||||
С |
|
|
A1 + A2 + A3 |
144 |
+56,52 −28,26 |
|
|
|
|
||||
|
|
|
= 864 +822,37 −73,5 |
= 9, 4см; |
||
|
|
|
|
172, 26 |
|
|
y |
|
= y1 A1 + y2 A2 + y3 A3 = 6 144 +6 56,52 −2,6 28,26 = |
||||
С |
|
A1 + A2 + A3 |
|
144 |
+56,52 −28,26 |
|
|
|
|
||||
|
|
|
= 864 +339,12 −73,5 |
= 6,6см. |
||
|
|
|
|
172, 26 |
|
|
Положение центра тяжести совпадает с точкой С {9,4; 6,6}
(рис. 5.11).
Статические моменты. Статические моменты сечения Sx и Sy определим, как сумму произведений элементарных площадей dAi на кратчайшее расстояния до осей Ox, Oy соответственно (рис. 5.11), т. е.
S x = ∑Ai yi → Sx = ∫y dA, Sy = ∑Ai xi → Sy = ∫x dA.
A A
115

И. В. Богомаз. Механика
Рис. 5.11
Статические моменты имеют размерность см3 или м3.
При параллельном переносе осей (Oxy → O1x1 y1 ) значения ста-
тических моментов изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, существует ось, относительно которой статический момент равен нулю.
Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей совпадает с точкой центра тяжести сечения.
Координаты центра тяжести тела через статические моменты будут вычисляться следующим образом:
x |
= |
Sy |
= ∑Ai xi →, |
y |
= |
Sx |
= ∑Ai yi . |
|
|
||||||
C |
A A |
C |
A |
A |
|||
|
|
|
|
||||
Пример 5.3. Для заданного несимметричного поперечного сечения, составленного из швеллера № 20 и неравнополочного уголка № 10/6,5 (рис. 5.12), найти положение центральных осей.
Рис. 5.12
116

5. Центр тяжести
Решение. Из сортамента выберем геометрические характеристики швеллера № 20 и неравнополочного уголка № 10/6,5 (табл. 5.1) и построим чертеж в масштабе (рис. 5.13).
Таблица 5.1
Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240–89)
|
|
|
|
|
I – момент инерции; |
|
||
|
h – высота швеллера; |
z0 – расстояние от оси y до на- |
||||||
|
b – ширина полки |
|
ружной грани стенки; |
|
||||
|
|
А – площадь поперечного сече- |
||||||
|
|
|
|
|
||||
|
|
|
|
|
ния |
|
|
|
|
Номер |
Размеры, |
|
|
|
|
||
|
швел- |
мм |
|
А, см2 |
Ix, см4 |
Iy, см4 |
x0, см |
|
|
лера |
h |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
200 |
|
76 |
23,4 |
1530 |
134 |
2,3 |
Уголки стальные горячекатаные неравнополочные. Сортамент (ГОСТ 8510–86)
В – ширина
большей полки; z0 – расстояние от оси y до наружной b – ширина грани стенки;
меньшей полки А – площадь поперечного сечения
|
Но- |
Разме- |
|
|
|
|
|
|
|
мер |
ры, мм |
А, см2 |
Ix, см4 |
Iy, см4 |
Ixy, см4 |
x0, см |
|
|
угол- |
В |
b |
|||||
|
|
|
|
|
|
|||
|
ка |
|
|
|
|
|
|
|
|
10/6,5 |
200 |
65 |
15,67 |
155,52 |
51,68 |
51,18 |
2,3 |
Для вычисления положения центра тяжести заданного сечения за вспомогательные оси примем центральные оси швеллера C1x1y1
(рис. 5.13).
Вычислим координаты центра тяжести сечения осей C1x1y1:
|
y |
= ∑Sxi |
= |
|
S1x1 |
+ S2x1 |
|
= |
А1 уС1 + А2 уС2 |
= |
0 +15,67 6,63 |
= 2,66; |
|||||
|
|
A1 |
+ A2 |
А1 + А2 |
23,4 +15,67 |
||||||||||||
|
C |
∑Ai |
|
|
|
|
|
|
|
|
|||||||
х |
= |
∑Sуi = |
S1у1 + S2 у1 |
= |
|
А1 хС1 + А2 хС2 |
= |
|
0 +15,67 (−3,94) |
= −1,58. |
|||||||
|
|
|
|
23,4 +15,67 |
|
||||||||||||
C |
∑Ai |
|
A1 + A2 |
|
|
А1 + А2 |
|
|
|
|
|||||||
117
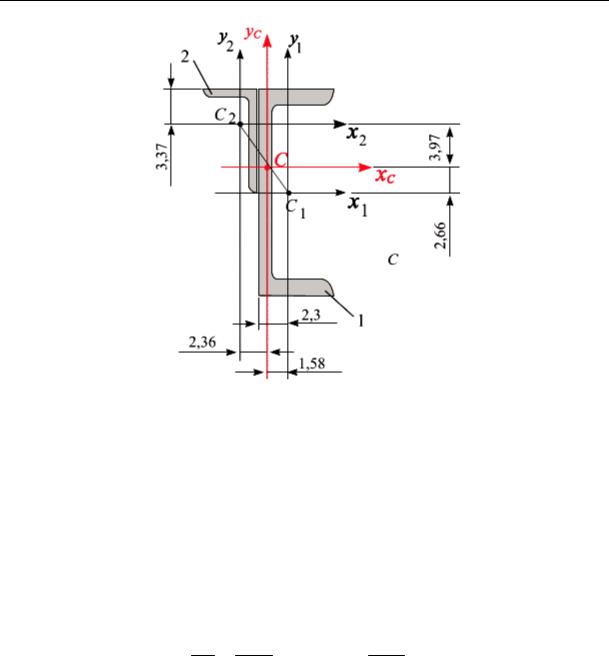
И. В. Богомаз. Механика
Рис. 5.13
Откладываем на схеме координаты точки центра тяжести сечения С{xC , yC }. Координаты центра тяжести сечения «легли» на отре-
зок С1С2, соединяющий центры тяжести частей (профилей), составляющих заданное сечение. Проверим правильность расчета. Соотношение отрезков должно быть равно соотношению площадей. Измеряем отрезки С1С и С2С, уточняем правильность соотношения
A2 = C1C →15,67 = C1C = 0,67.
A1 C2C 23,4 C2C
Проводим центра центральные оси CxCyC (рис. 5.13).
118
