
- •Змістовий модуль 2
- •2. Основні властивості невизначеного інтеграла Враховуючи означення невизначеного інтеграла
- •3. Таблиця найпростіших інтегралів
- •4. Незалежність виду невизначеного інтеграла від вибору аргументу
- •6. Комплексні числа.
- •3. Інтегрування дробів
- •4.Інтегрування найпростіших ірраціональностей
- •5. Підстановки Ейлера
- •6. Інтегрування диференціальних біномів
- •7. Інтегрування тригонометричних функцій
- •Семінарське заняття 11
- •Тема 10. Визначений інтеграл. Невласні інтеграли. Кратні інтеграли
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Визначений інтеграл. Невласні інтеграли 1-го і 2-го роду
- •1. Визначений інтеграл та його геометрична інтерпретація
- •2. Властивості визначеного інтеграла
- •3. Формула Ньютона-Лейбніца
- •4. Наближене обчислення інтеграла
- •5. Невласні інтеграли першого і другого роду. Поняття про кратні інтеграли
- •Наприклад
- •Наприклад. Інтеграл – абсолютно збіжний інтеграл, оскільки, а– збіжний інтеграл (читачеві рекомендується перевірити це самостійно).
- •6. Застосування визначеного інтегралу
- •Економічні застосування інтегралів
- •Семінарське заняття 12
- •Тема 11. Числові ряди
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •2. Властивості збіжних рядів
- •Дійсно, якщо –– на частинна сума ряду (1), а–– на частинна сума ряду (2), то , і.
- •Якщо ряд (1) збігається, то його – ний член прямує до нуля при необмеженому зростанні.
- •Семінарське заняття 13
- •2. Інтервал і радіус збіжності.
- •3. Властивості степеневих рядів
- •Так, якщо
- •4. Ряди Тейлора і Маклорена. Приклади
- •Підкреслимо, що ряд Тейлора представляє дану функцію тільки тоді, коли(в противному випадку ряд може збігатися до іншої функції). Наведемо кілька важливих рядів Маклорена
- •Ряди по ортогональних функціях
- •Ряди Фур'є Функціональний ряд
- •Розглянемо ряд
- •2. Властивості функціональних рядів
- •Семінарське заняття 14
- •Тема 13. Загальні відомості про диференціальні рівняння. Деякі типи диференціальних рівнянь першого порядку
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Семінарське заняття 15
- •Тема 14. Диференціальні рівняння вищих порядків
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Рівняння виду
- •Семінарське заняття 17
- •Семінарське заняття 18
- •Тема 14. Диференціальні рівняння вищих порядків. Лдр вищого порядку з правою частиною спеціального виду
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •9.1. Основні поняття
6. Інтегрування диференціальних біномів
Інтеграл
від диференціального бінома
![]() (
(![]() – раціональні числа,
– раціональні числа,![]() – сталі) зводиться до інтеграла від
раціональної функції і, отже, виражається
через елементарні функції в таких трьох
випадках:
– сталі) зводиться до інтеграла від
раціональної функції і, отже, виражається
через елементарні функції в таких трьох
випадках:
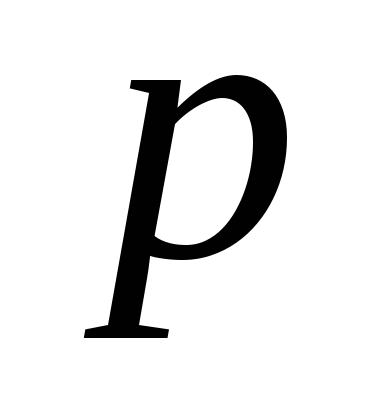 –ціле
число (тобто додатне, від’ємне ціле
число чи число нуль);
–ціле
число (тобто додатне, від’ємне ціле
число чи число нуль);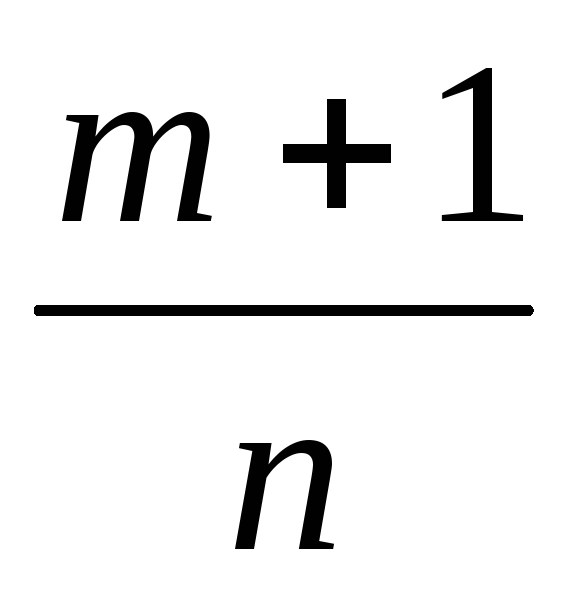 –ціле
число;
–ціле
число;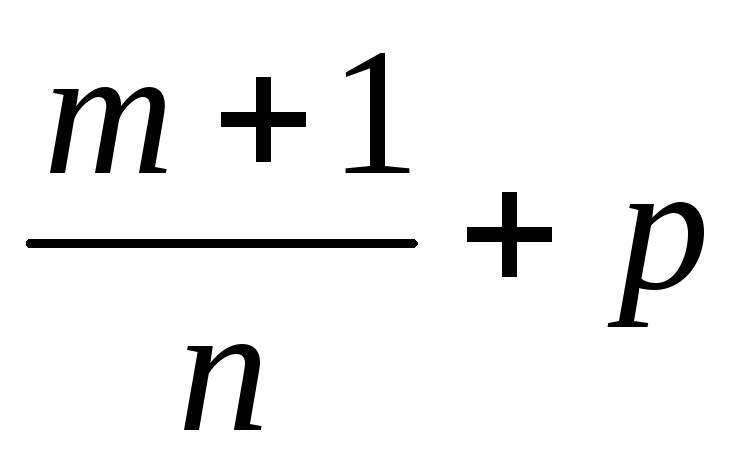 –ціле
число.
–ціле
число.
У всіх інших випадках, як довів Чебишев, інтеграл не може бути виражений через елементарні функції.
Якщо
![]() – ціле число, то ситуація зводиться до
розглянутого вище випадку І в п. 1 даної
лекції. Якщо
– ціле число, то ситуація зводиться до
розглянутого вище випадку І в п. 1 даної
лекції. Якщо![]() – ціле число, то слід виконати заміну
змінних
– ціле число, то слід виконати заміну
змінних![]() ,
де
,
де![]() – знаменник числа
– знаменник числа![]() .
Якщо ж
.
Якщо ж![]() – ціле число, то слід виконати заміну
змінних
– ціле число, то слід виконати заміну
змінних![]() (
(![]() – знаменник числа
– знаменник числа![]() ).
).
Наприклад.
Знайти
інтеграл
![]()
Розв’язок.
Тут
![]() Ми зустрічаємося, з тією ситуацією, коли
Ми зустрічаємося, з тією ситуацією, коли![]() – ціле число. Отже, виконуємо заміну
– ціле число. Отже, виконуємо заміну![]() Звідси отримаємо:
Звідси отримаємо:![]() Отже,
Отже,![]() а це – простий інтеграл від раціональної
функції. Маємо:
а це – простий інтеграл від раціональної
функції. Маємо: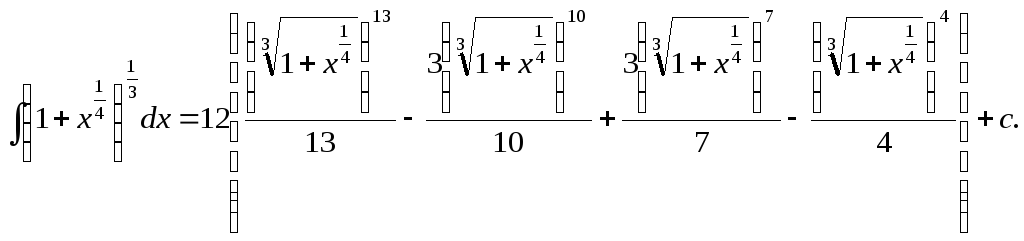
7. Інтегрування тригонометричних функцій
Розглянемо
інтеграл виду
![]() Цей інтеграл за допомогоюуніверсальної
тригонометричної підстановки
Цей інтеграл за допомогоюуніверсальної
тригонометричної підстановки
![]() зводиться до інтеграла від раціональної
функції.
зводиться до інтеграла від раціональної
функції.
Дійсно, маємо:
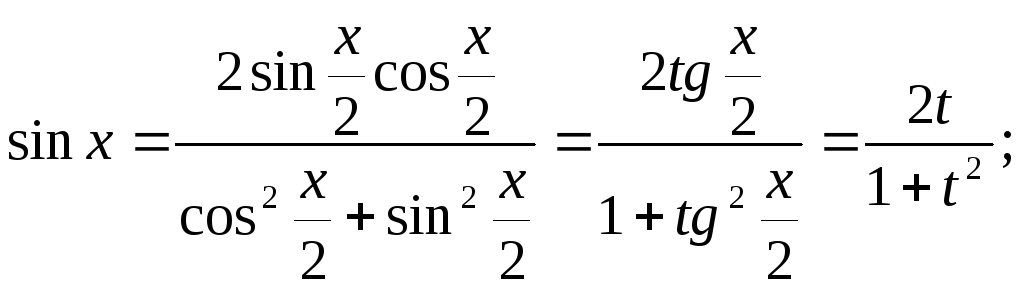
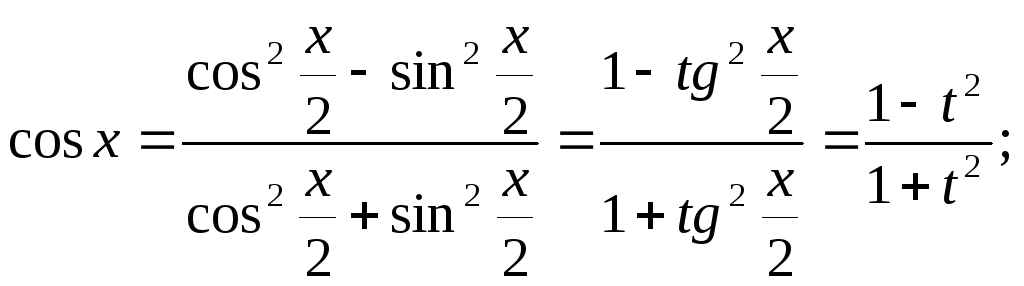
![]() Таким
чином, інтеграл
Таким
чином, інтеграл
![]() раціонально виражається через
раціонально виражається через![]() .
.
Наприклад.
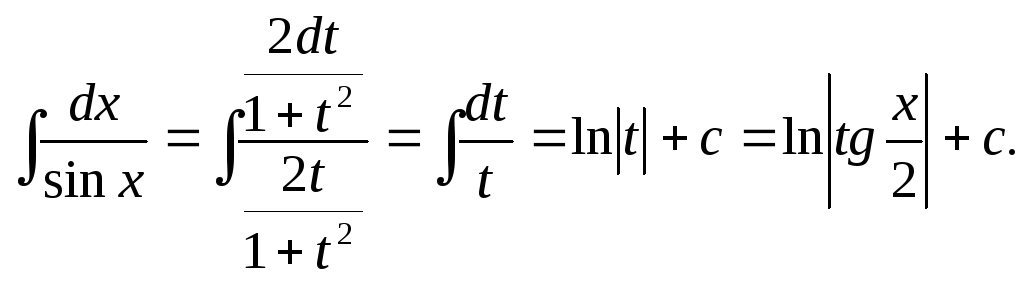
В деяких випадках більш доцільно користуватися не універсальною тригонометричною підстановкою (якщо вона призводить до громіздких виразів під знаком інтеграла), а іншими методами.
Інтеграл виду
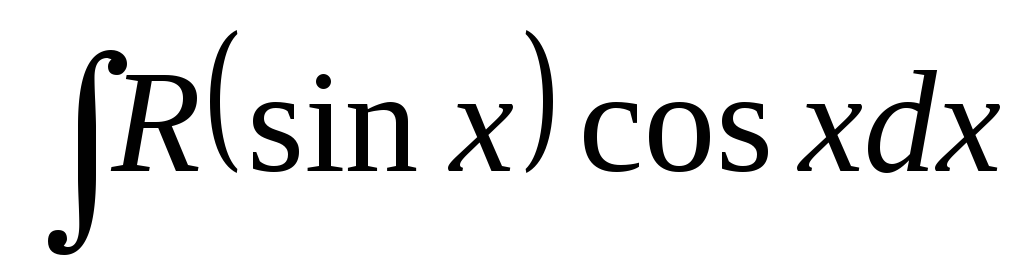 зручно знаходити за допомогою
тригонометричної підстановки
зручно знаходити за допомогою
тригонометричної підстановки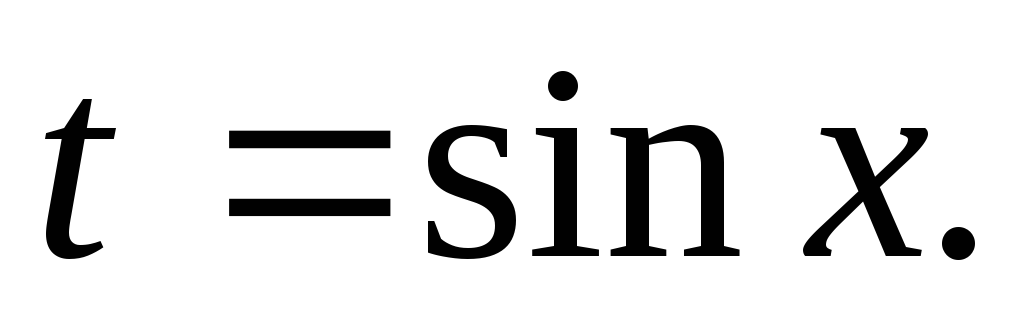 Тоді
Тоді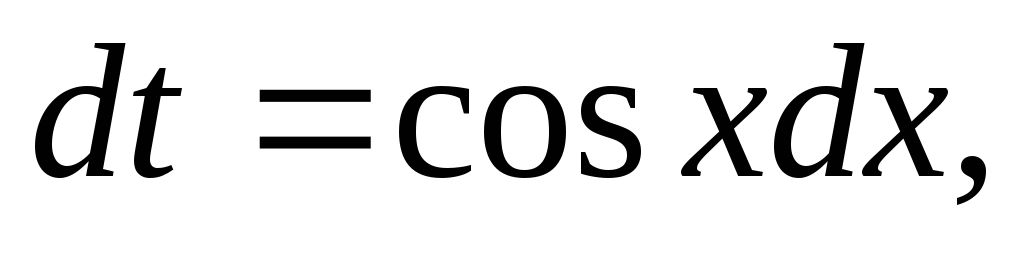 і ми одержуємо
і ми одержуємо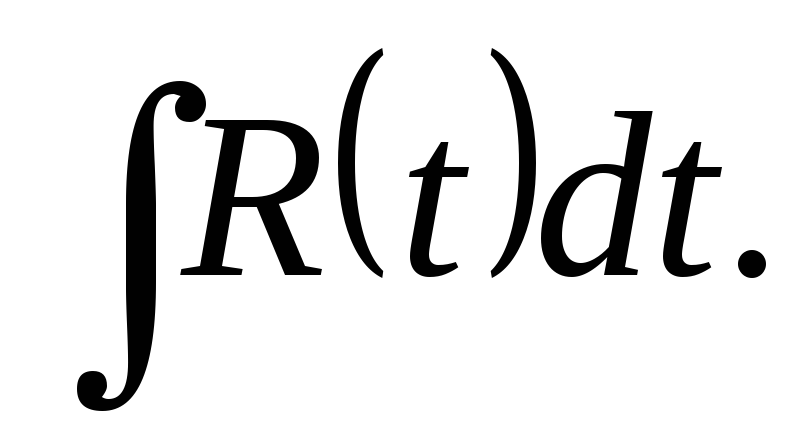
Аналогічно задача знаходження інтеграла виду
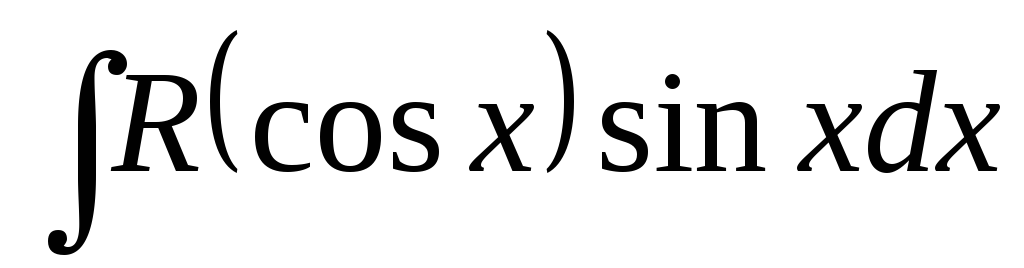 розв’язується шляхом введення
підстановки
розв’язується шляхом введення
підстановки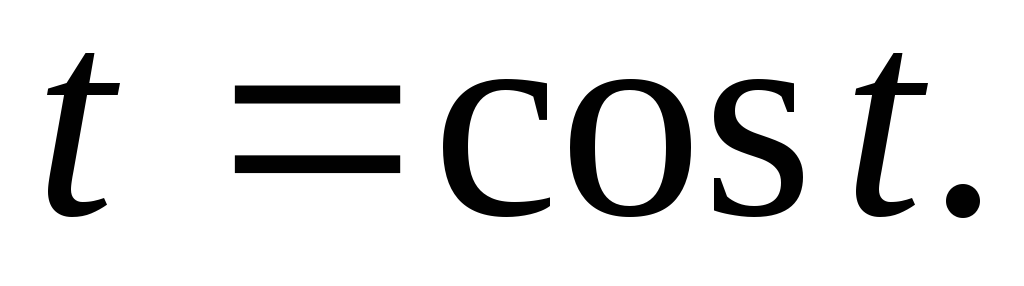
Щоб перейти від інтеграла
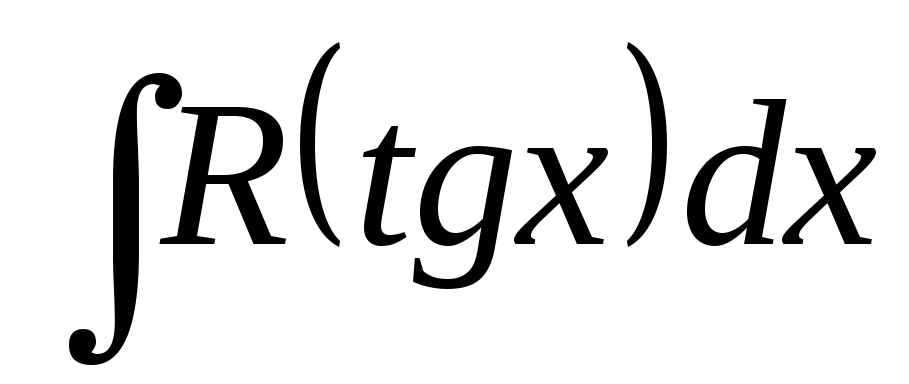 до інтеграла від раціональної функції,
досить виконати підстановку
до інтеграла від раціональної функції,
досить виконати підстановку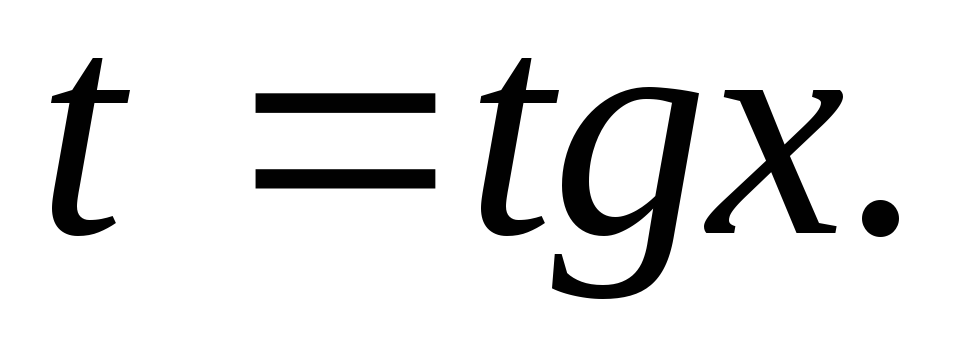 Дійсно при цьому
Дійсно при цьому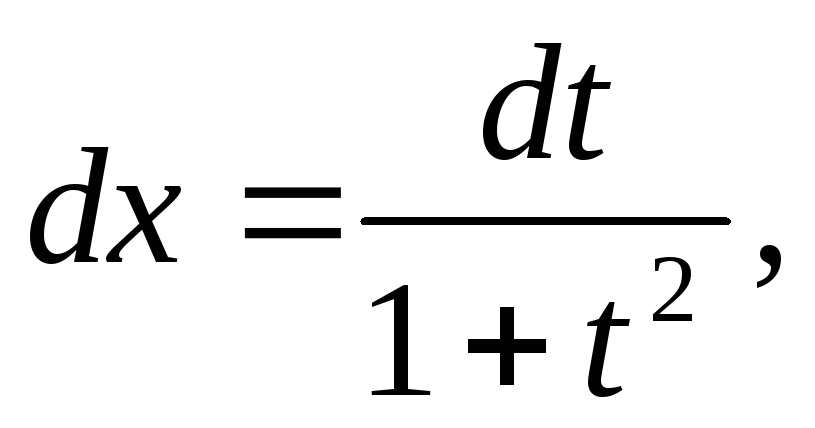 і ми одержуємо інтеграл від раціональної
функції виду
і ми одержуємо інтеграл від раціональної
функції виду
![]()
Якщо
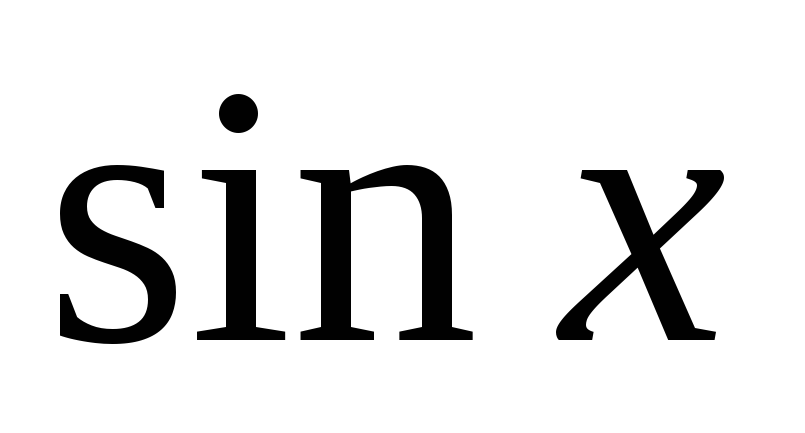 та
та містяться під знаком інтеграла
містяться під знаком інтеграла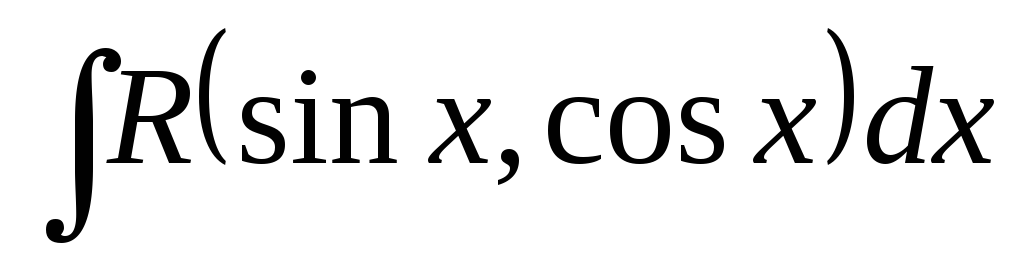 лише в парних степенях, то доцільною є
підстановка
лише в парних степенях, то доцільною є
підстановка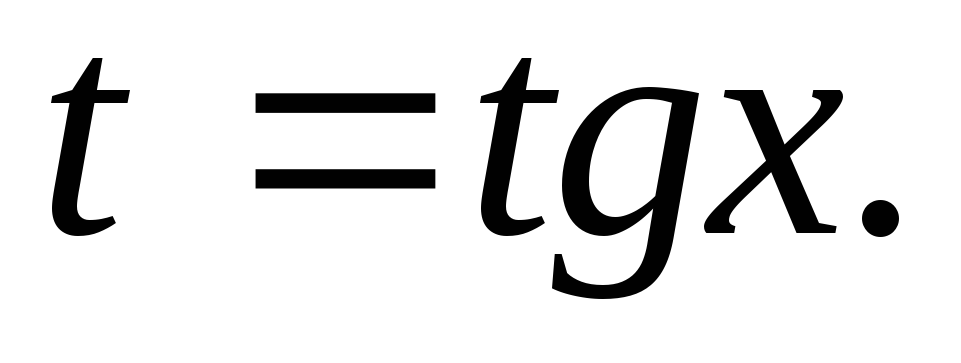 При цьому
При цьому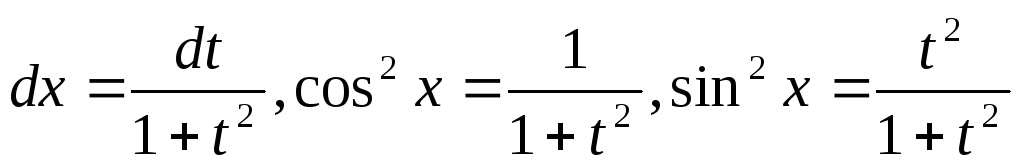 .
.Розглянемо інтеграл виду
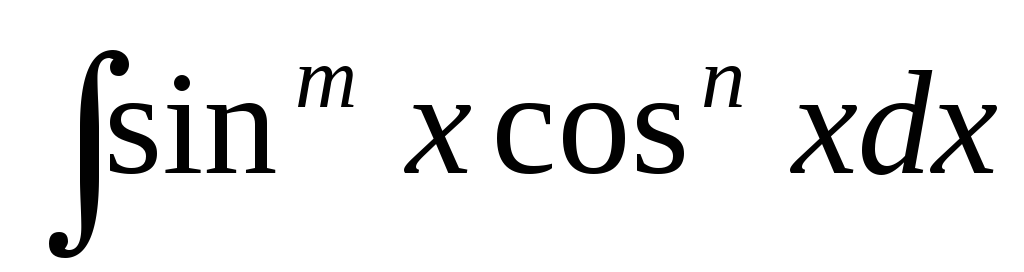 (
(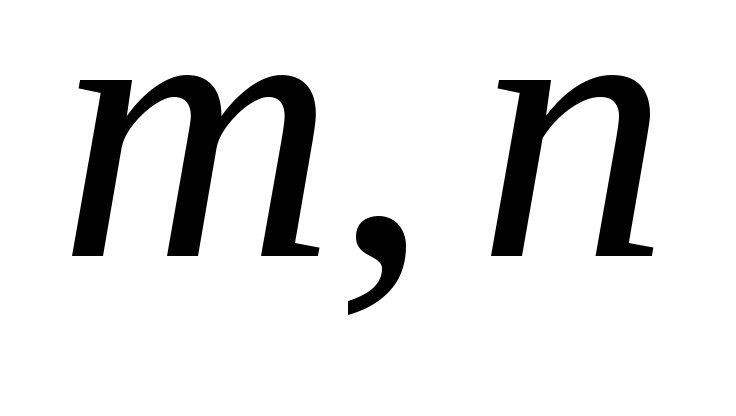 – цілі числа). Можливі такі випадки:
– цілі числа). Можливі такі випадки:Хоч одне з чисел
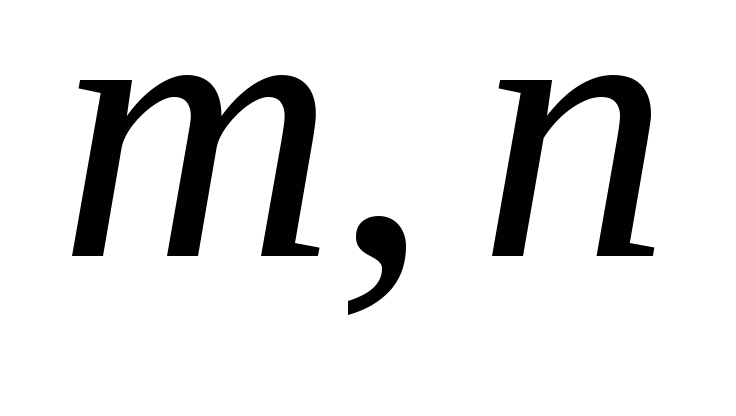 непарне. Проілюструємо хід міркувань
на такому прикладі.
непарне. Проілюструємо хід міркувань
на такому прикладі.
![]()
Таким
чином, ввівши підстановку
![]() приходимо до інтеграла від раціональної
функції.
приходимо до інтеграла від раціональної
функції.
7)
Числа,
![]() – невід’ємні і парні.
– невід’ємні і парні.
Доречно скористатися відомими формулами тригонометрії.
![]()
Наприклад.
Знайдемо інтеграл
![]() .
.
Маємо:
![]()
![]() .
.
Числа
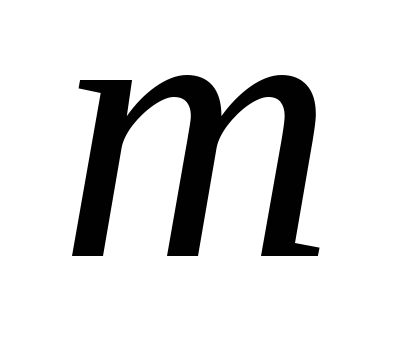 і
і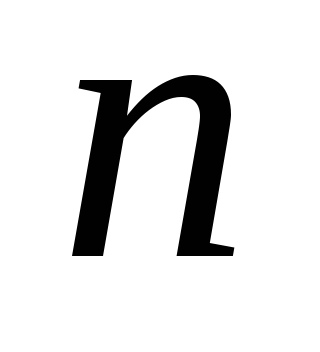 парні, але хоча б одне з них – від’ємне.
парні, але хоча б одне з них – від’ємне.
В
цьому випадку зручно скористатися
заміною
![]() або
або![]() .
.
Інтеграли виду
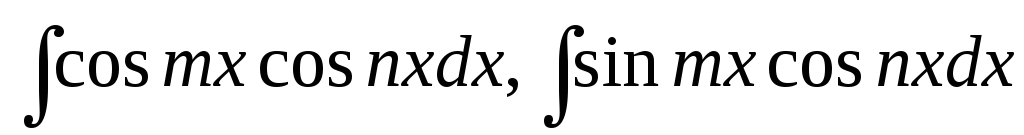 та
та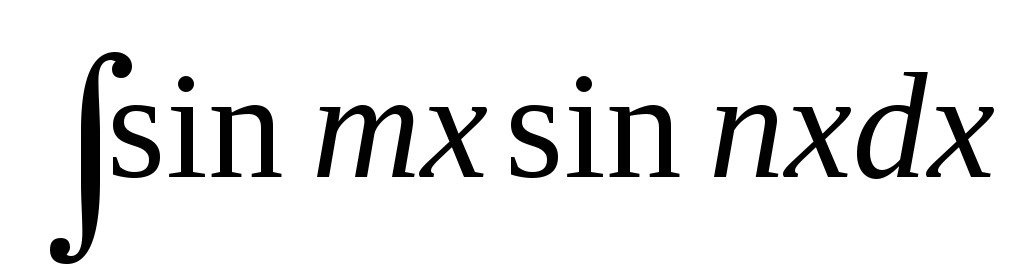 легко знайти, якщо перетворити
підінтегральні добутки в суми:
легко знайти, якщо перетворити
підінтегральні добутки в суми:
![]()
![]() ,
,
![]()
Зауваження. Будь-яка неперервна на деякому інтервалі функція має на цьому інтервалі первісну, але не всяка первісна виражається через елементарні функції в скінченому вигляді. Це стосується, наприклад, таких інтегралів:
![]() та
ін.
та
ін.
Для
практичних застосувань складають
таблиці значень таких функцій при різних
![]() .
Наприклад, в курсі теорії ймовірностей
та математичної статистики ми будемо
зустрічатися з функцією Лапласа
.
Наприклад, в курсі теорії ймовірностей
та математичної статистики ми будемо
зустрічатися з функцією Лапласа![]() та користуватимемося таблицею значень
цієї функції при різних
та користуватимемося таблицею значень
цієї функції при різних![]() .
.
Семінарське заняття 11
Тема 10. Визначений інтеграл. Невласні інтеграли. Кратні інтеграли
Питання для усного опитування та дискусії
10.1. Визначений інтеграл (означення, властивості, способи обчислення).
10.2. Невласні інтеграли першого і другого роду.
10.3. Подвійні та потрійні інтеграли, їх властивості, способи обчислення.
10.4. Застосування інтегралів.
Аудиторна письмова робота
