Ряди Фур'є Функціональний ряд

(4)

де – сталі числа, називаєтьсятригонометричним рядом.

Відзначимо основні властивості тригонометричних рядів.

а) Сума тригонометричного ряду (4) – періодична функція з періодом .

б) Якщо числовий ряд збігається абсолютно, то тригонометричні рядитазбігаються рівномірно на всій числовій осі.

в) Якщо тригонометричний ряд (4) збігається рівномірно на відрізку до функції, то

, ,

.

Нехай – деяка періодична функція періодуT=2. Тригонометричний ряд

називається рядом Фур'є для функції , якщо коефіцієнти цього ряду знаходяться за формулами типу (3):

(тобто ),

Функціональні ряди (загальна теорія)

1. Функціональний ряд та його збіжність

Розглянемо ряд

(1)

членами якого є функції; задані на інтервалі . Щоб відповісти на питання, в якому розумінні частинна суманаближається до суми, розглянемо поняття про відхилення двох функцій.

Нехай дві функції, і, задані на одному і тому ж скінченому інтервалі.Рівномірним відхиленням їх одна від другої називається величина середнім інтегральним відхиленням функцій таназивається величинаДеколи користуютьсясереднім квадратичним відхиленням: . Зустрічаються і інші види відхилень.

Говорять, що ряд (1) збігається на даному інтервалі до функції – суми ряду, якщо відхилення частинної сумивідпрямує до нуля при зростанні. При цьому ряд (1) збігається до сумирівномірно, якщо в середньому, якщо в середньому квадратичному, якщо 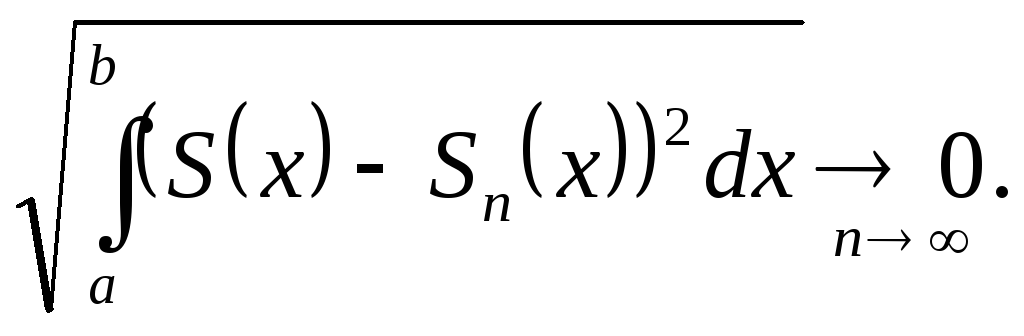Зауважимо, що коли, ряд (1) збігається рівномірно, то він збігається також в середньому та в середньому квадратичному, причому до тієї ж суми.

Вейєрштрасс довів, що коли всі , причому, то ряд (1) рівномірно збігається.

Сукупність тих значень , при яких функціональний ряд збігається, називаєтьсяобластю збіжності цього ряду.

Приклад №1. Функціональний ряд

збігається при , і його сума дорівнює. Отже,

2. Властивості функціональних рядів

Відзначимо основні властивості рівномірно збіжних функціональних рядів.

1) Сума рівномірно збіжного ряду з неперервних функцій – неперервна функція.

Дійсно, якщо ,

то

.

Функція неперервна як сума скінченого числа неперервних функцій. при досить великих значенняхзалишокбуде як завгодно малий при– це випливає із рівномірної збіжності ряду. Отже, малому приростувідповідає як малий приріст, так і малий приріст. Значить, і вся сумазміниться мало, що і доводить її неперервність.

Зауважимо, що коли ряд (1) збігається рівномірно, то його сума може мати розриви лише в тих точках, в яких мали розриви доданки. Якщо ж ряд збігається в середньому, то його сума може мати і інші розриви, а також бути розривною, якщо всі члени ряду – неперервні.

2) Якщо ряд збігається рівномірно, то його можна почленно інтегрувати:

,

причому одержаний в результаті інтегрування ряд рівномірно збігається на інтервалі .

Дійсно,

.

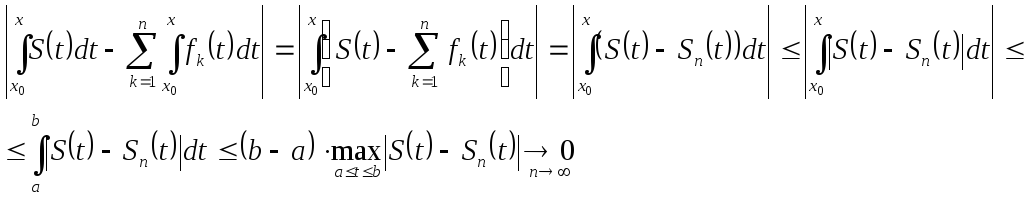3) Ряд із неперервних функцій, що рівномірно збігається, можна почленно диференціювати, якщо після цього одержується ряд, який збігається рівномірно:

Дійсно, нехай .

Інтегруючи почленно цей ряд на основі попередньої властивості, маємо:

.

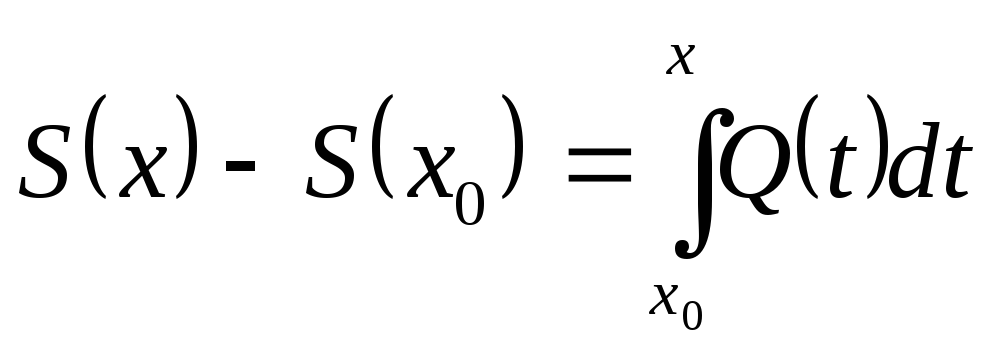Диференціюючи цю рівність по , знаходимо:. Властивість доведена.