
- •Змістовий модуль 2
- •2. Основні властивості невизначеного інтеграла Враховуючи означення невизначеного інтеграла
- •3. Таблиця найпростіших інтегралів
- •4. Незалежність виду невизначеного інтеграла від вибору аргументу
- •6. Комплексні числа.
- •3. Інтегрування дробів
- •4.Інтегрування найпростіших ірраціональностей
- •5. Підстановки Ейлера
- •6. Інтегрування диференціальних біномів
- •7. Інтегрування тригонометричних функцій
- •Семінарське заняття 11
- •Тема 10. Визначений інтеграл. Невласні інтеграли. Кратні інтеграли
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Визначений інтеграл. Невласні інтеграли 1-го і 2-го роду
- •1. Визначений інтеграл та його геометрична інтерпретація
- •2. Властивості визначеного інтеграла
- •3. Формула Ньютона-Лейбніца
- •4. Наближене обчислення інтеграла
- •5. Невласні інтеграли першого і другого роду. Поняття про кратні інтеграли
- •Наприклад
- •Наприклад. Інтеграл – абсолютно збіжний інтеграл, оскільки, а– збіжний інтеграл (читачеві рекомендується перевірити це самостійно).
- •6. Застосування визначеного інтегралу
- •Економічні застосування інтегралів
- •Семінарське заняття 12
- •Тема 11. Числові ряди
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •2. Властивості збіжних рядів
- •Дійсно, якщо –– на частинна сума ряду (1), а–– на частинна сума ряду (2), то , і.
- •Якщо ряд (1) збігається, то його – ний член прямує до нуля при необмеженому зростанні.
- •Семінарське заняття 13
- •2. Інтервал і радіус збіжності.
- •3. Властивості степеневих рядів
- •Так, якщо
- •4. Ряди Тейлора і Маклорена. Приклади
- •Підкреслимо, що ряд Тейлора представляє дану функцію тільки тоді, коли(в противному випадку ряд може збігатися до іншої функції). Наведемо кілька важливих рядів Маклорена
- •Ряди по ортогональних функціях
- •Ряди Фур'є Функціональний ряд
- •Розглянемо ряд
- •2. Властивості функціональних рядів
- •Семінарське заняття 14
- •Тема 13. Загальні відомості про диференціальні рівняння. Деякі типи диференціальних рівнянь першого порядку
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Семінарське заняття 15
- •Тема 14. Диференціальні рівняння вищих порядків
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Рівняння виду
- •Семінарське заняття 17
- •Семінарське заняття 18
- •Тема 14. Диференціальні рівняння вищих порядків. Лдр вищого порядку з правою частиною спеціального виду
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •9.1. Основні поняття
3. Властивості степеневих рядів
Відзначимо основні властивості степеневих рядів.
Сума степеневого ряду є функція, неперервна в інтервалі збіжності ряду. Відзначимо, що в тому кінці інтервалу, де степеневий ряд збігається, його сума також неперервна.
Степеневий ряд можна почленно інтегрувати в інтервалі збіжності.
Так, якщо
![]()
то
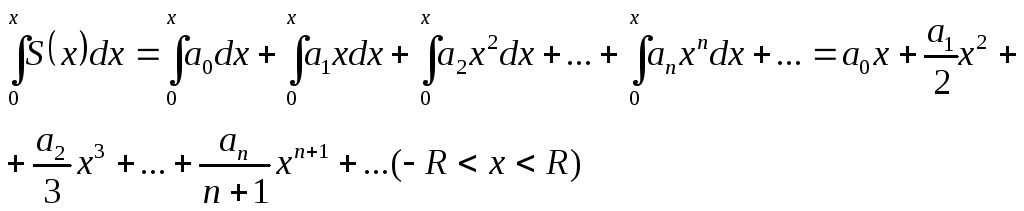
Степеневий ряд можна почленно інтегрувати в інтервалі збіжності.
![]()
Продовжуючи послідовно диференціювання, одержимо:
![]()
![]() і
так далі. Степеневий ряд в інтервалі
його збіжності можна почленно
диференціювати будь-яке число раз. При
цьому інтервал збіжності кожного ряду,
одержаного в результаті диференціювання,
є той же інтервал
і
так далі. Степеневий ряд в інтервалі
його збіжності можна почленно
диференціювати будь-яке число раз. При
цьому інтервал збіжності кожного ряду,
одержаного в результаті диференціювання,
є той же інтервал
![]() .
.
4. Ряди Тейлора і Маклорена. Приклади
Для
функції
![]() ,
яка має всі похідні до
,
яка має всі похідні до![]() -го
порядку включно, в околі точки
-го
порядку включно, в околі точки![]() має місце вже відома нам формула Тейлора:
має місце вже відома нам формула Тейлора:
![]()
![]()
де
залишковий член
![]() обчислюється за формулою:
обчислюється за формулою:
![]()
Припустимо, що і
функція
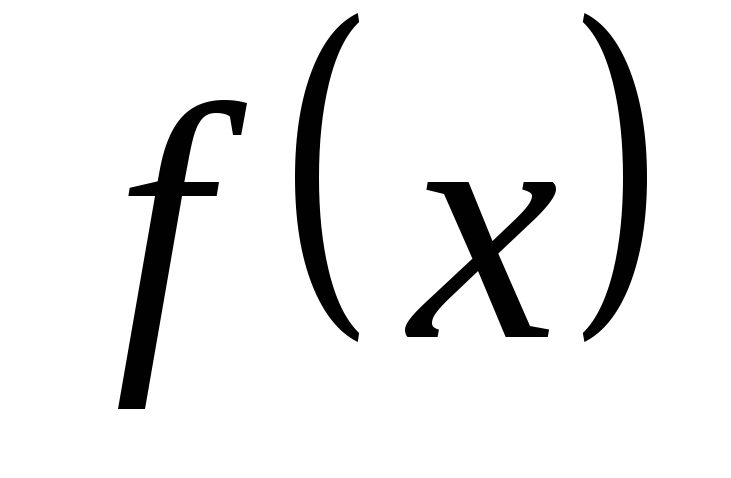 має похідні всіх порядків в околі точки
має похідні всіх порядків в околі точки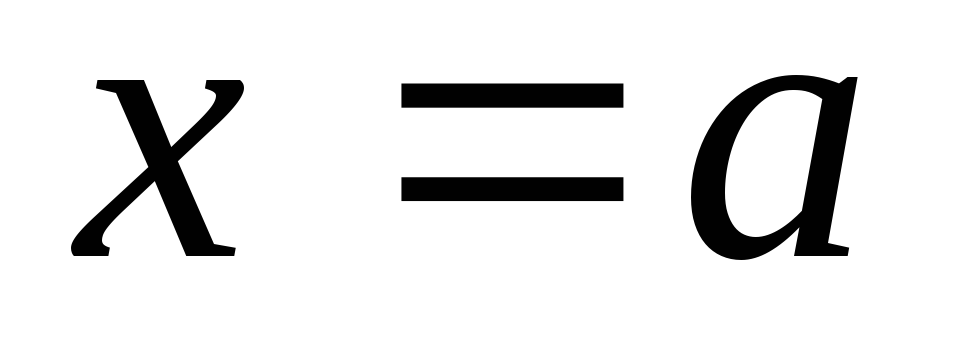 ;
;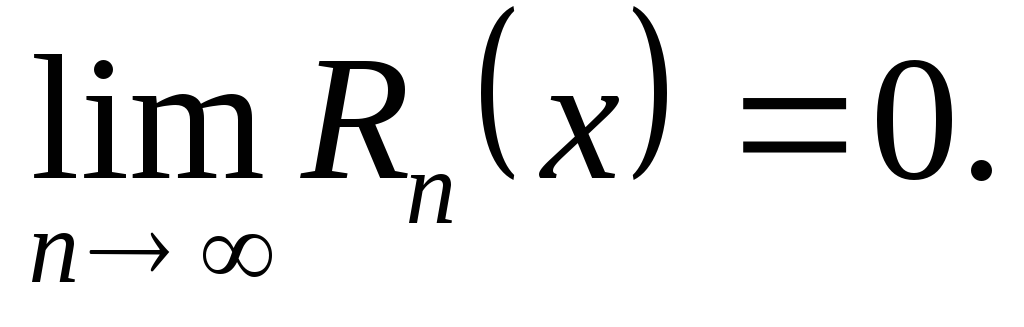
Представимо формулу
![]() у вигляді
у вигляді
![]() ,
,
![]()
де
![]()
Перейдемо до границі у формулі (6):
![]() звідки
одержуємо:
звідки
одержуємо:
![]()
Отже,
![]()
![]()
Нескінченний
ряд
![]() називаєтьсярядом
Тейлора (при
називаєтьсярядом
Тейлора (при
![]() – рядом Маклорена).
– рядом Маклорена).
Підкреслимо, що ряд Тейлора представляє дану функцію тільки тоді, коли(в противному випадку ряд може збігатися до іншої функції). Наведемо кілька важливих рядів Маклорена
![]()
![]()
Приклад
№2.
Розкладемо в ряд Маклорена функцію
![]() .
.
Оскільки
![]() і
і![]() то ряд Маклорена для функції
то ряд Маклорена для функції![]() має вигляд:
має вигляд:
![]() .
.
Приклад
№3.
Розкладемо в ряд Маклорена функцію
![]() .
.
Аналогічно прикладу №2 мажмо:
![]()
Цей
ряд збігається при всіх значеннях
![]() до функції
до функції![]() .
.
Приклад
№4.
Розкладемо в ряд Маклорена функцію
![]()
![]() .
.
Цей
ряд збігається при
![]() .
.
Зокрема,
при
![]() маємо:
маємо:
![]()
![]() ,
при
,
при
![]() –
–
![]() при
при
![]() –
–
![]()
![]()
Приклад
№6.
Одержимо ряд Маклорена для функції
![]() .
.
Для цього застосуємо теорему про інтегрування степеневих рядів до ряду
![]()
Маємо:
![]() і, отже,
і, отже,
![]()
Приклад№7.
Ряд Маклорена для функції
![]() одержується шляхом інтегрування ряду
одержується шляхом інтегрування ряду
![]()
в
межах від 0 до
![]()
![]() :
:
![]() .
.
Приклад
№8.
Розкладемо в ряд Маклорена функцію
![]()
Використовуючи
біномний розподіл функції
![]() та замінивши
та замінивши![]() на
на![]() ,
будемо мати:
,
будемо мати:![]()
Оскільки
![]() ,
то, інтегруючи останній ряд, будемо
мати:
,
то, інтегруючи останній ряд, будемо
мати:
![]() .
.
Ряди по ортогональних функціях
Дамо
означення ортогональних функцій. Дві
дійсні функції
![]() та
та![]() ,
задані на скінченому або нескінченному
інтервалі
,
задані на скінченому або нескінченному
інтервалі![]() ,
називаютьсяортогональними
одна одній на цьому інтервалі, якщо
,
називаютьсяортогональними
одна одній на цьому інтервалі, якщо
![]() (вважаємо, що функції
(вважаємо, що функції![]() та
та![]() абсолютно інтегровані). система функцій
називається ортогональною на деякому
інтервалі, якщо кожні дві функції з цієї
системи ортогональні одна одній на
цьому інтервалі.
абсолютно інтегровані). система функцій
називається ортогональною на деякому
інтервалі, якщо кожні дві функції з цієї
системи ортогональні одна одній на
цьому інтервалі.
Приклад
№1.
Ортогональною є система функцій 1,
![]()
![]() на інтервалі
на інтервалі![]() .
Це дійсно так, оскільки при
.
Це дійсно так, оскільки при![]() виконуються умови:
виконуються умови:
![]()
при
будь-яких
![]() – умова
– умова![]() .
Ортогональною на інтервалі
.
Ортогональною на інтервалі![]() є система функцій
є система функцій
![]() .
.
Приклад
№2.
При
![]() ортогональні один одному многочлени
Лежандра:
ортогональні один одному многочлени
Лежандра:
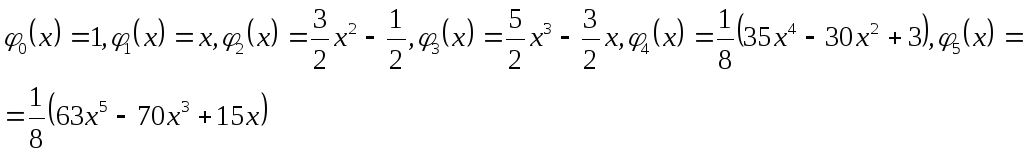 і
т.д.
і
т.д.
Вивчимо
питання про ряди по ортогональних на
проміжку
![]() функціях
функціях![]() тобто про ряди виду
тобто про ряди виду![]() де
де![]() – числові коефіцієнти.
– числові коефіцієнти.
Якщо
представлення (2) можливе для будь-якої
скінченої функції
![]() ,
то система функцій
,
то система функцій![]()
![]() називаєтьсяповною.
називаєтьсяповною.
Нехай
жодна з функцій
![]() не дорівнює тотожно нулю. Знайдемо
коефіцієнти
не дорівнює тотожно нулю. Знайдемо
коефіцієнти![]() в формулі (2). Для цього помножимо обидві
частини цієї рівності на
в формулі (2). Для цього помножимо обидві
частини цієї рівності на![]() та про інтегруємо результат по інтервалу
та про інтегруємо результат по інтервалу![]() :
:
![]()
В
силу ортогональності системи функцій
![]() майже всі інтеграли справа (крім одного)
перетворюються в нуль. Звідси одержуємо
формулу для коефіцієнтів
майже всі інтеграли справа (крім одного)
перетворюються в нуль. Звідси одержуємо
формулу для коефіцієнтів
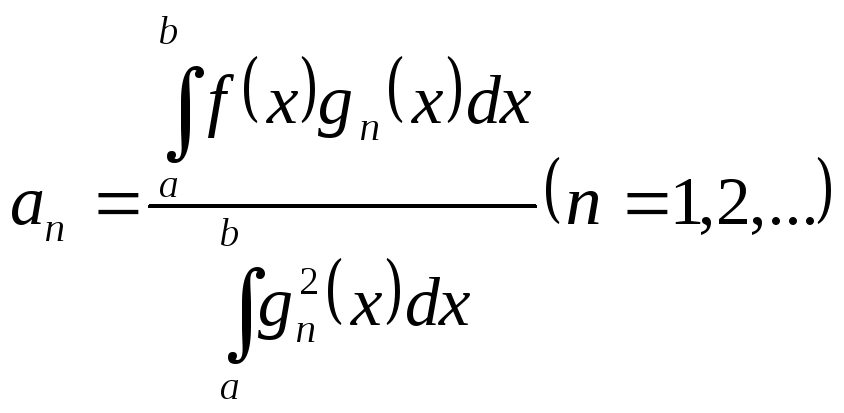 (3)
(3)
