Вариант № 6

1. Для данного определителя найти миноры и алгебраические дополнения элементов. Вычислить определитель: а) разложив его по элементамi-ой строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-ой строки.

i = 1, j = 2

2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г).

3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

4. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

5. Решить однородную систему линейных алгебраических уравнений.

6. Решить однородную систему линейных алгебраических уравнений.

Вариант № 7

1. Для данного определителя найти миноры и алгебраические дополнения элементов. Вычислить определитель: а) разложив его по элементамi-ой строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-ой строки.

i = 2, j = 3

2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г).

3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

4. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

5. Решить однородную систему линейных алгебраических уравнений.

6. Решить однородную систему линейных алгебраических уравнений.

Вариант № 8

1. Для данного определителя найти миноры и алгебраические дополнения элементов. Вычислить определитель: а) разложив его по элементамi-ой строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-ой строки.

i = 3, j = 2

2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г).

3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

4. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

5. Решить однородную систему линейных алгебраических уравнений.

6. Решить однородную систему линейных алгебраических уравнений.

Вариант № 9

1. Для данного определителя найти миноры и алгебраические дополнения элементов. Вычислить определитель: а) разложив его по элементамi-ой строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-ой строки.

i = 4, j = 3

2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г).

3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

4. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

5. Решить однородную систему линейных алгебраических уравнений.

6. Решить однородную систему линейных алгебраических уравнений.

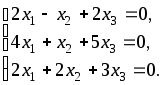
Вариант № 10

1. Для данного определителя найти миноры и алгебраические дополнения элементов. Вычислить определитель: а) разложив его по элементамi-ой строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-ой строки.

i = 4, j = 2

2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г).

3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

4. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

5. Решить однородную систему линейных алгебраических уравнений.

6. Решить однородную систему линейных алгебраических уравнений.