Примеры решения типовых задач

Свойства сходящихся последовательностей

Последовательность, имеющая предел, называется сходящейся,а последовательность, не имеющая предела, называетсярасходящейся.

• Сходящаяся последовательность имеет только один предел.

• Сходящаяся последовательность ограничена.

Вычислить пределы числовых последовательностей

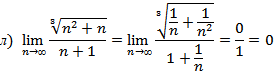
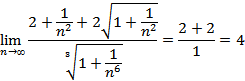
Основные свойства пределов функций

1. , где С =const.

2. 

3. 

4. 

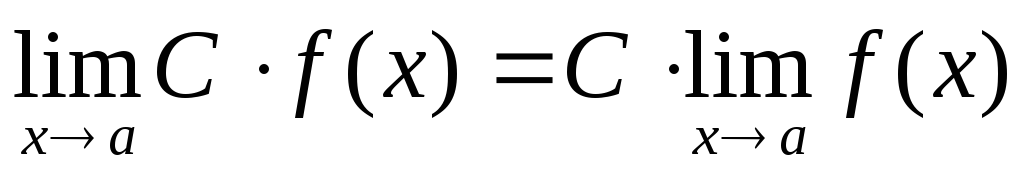
Вычислить предел функции в точке

Найти производные функций:

1)

2)

4)

а) - производная произведения двух функций

б) - производная отношения двух функций

в) - производная суммы двух сложных функций

Найти производную функции второго порядка:

Составить уравнение касательной и нормали к графику функции в точке:

Исследовать функцию и построить ее график.

• D(у) = (-; -1)(-1; 1)(1;).

В свою очередь, прямые х= 1,х= -1 являютсявертикальными асимптотамикривой.

Е(у) = (-;).

• Точками разрывафункции являются точких= 1,х= -1.

• Если у = 0, то=0х=0 – проходит через начало координат

Если х = 0, тоу ==0у=0

• Проверим на четность: у(-х) === -у(х) –функция нечетная, следовательно график симметричен относительно начал координат.

• Найдем производную функции

Критические точки: x= 0;x= -;x= ;x= -1;x= 1 и помечаем их на числовой прямой

+ - - - - + y ’

--1* 0* 1*х

y

max min

y_max(-) =и y_min() =

• Найдем вторую производную функции

.

Определим выпуклость и вогнутость кривой на промежутках х=0,х = -1,х =1

- + - + f’’

-1 0 1x

f

• Про вертикальные асимптотыбыло уже сказано выше. Теперь найдемнаклонные асимптоты.

Итого, уравнение наклонной асимптоты – y=x.

• Построимграфикфункции:

Свойства неопределенного интеграла:

1. 

2. производная неопределенного интеграла равна подынтегральной функции;

3. - интегрирование – действие обратное дифференцированию с точностью доconst;

4. , гдеu,v– некоторые функции отх;

5. 

6. Если F(x) - первообразная дляf(x), то– первообразная для

Непосредственное интегрирование

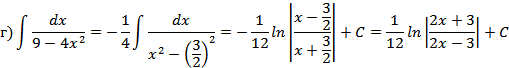
Метод замены переменной

Метод интегрирования по частям

Свойства определенного интеграла

Найти площадь плоской фигуры

_б)

_{Найдем точки пересечения функций, ограничивающих на плоскости фигуру, которая разбивается на 2 фигуры:}

Следует учесть, что фигура ограничена горизонтальной прямой, т.е. при нахождении площади криволинейной трапеции необходимо вычесть площадь квадрата, не включенного в фигуру.

Найти объемы тел, образованных при вращении вокруг осей Ох и Оу плоских фигур, ограниченных линиями: