shporapowushci

7. Теорема про проміжну послідовність.

Нехай при такій умові, що

існує тоді послідовність - збіжна і її границя = a. Оскільки

Оскільки

Згадаймо про теорему ,

Достатня умова існування гр. пос Якщо послідовність монотонно не спадна, обмежена зверху (або монотонно не зростаюча, обмежена знизу), то в неї є границя.

9. Границя ф-ції у т. за Коші і Гейне, при x до нескінченності.

Гейне. Нехай ф-ція f(x) визначена в деякому околі точки а, за виключенням можливо самої точки. Тоді А – назив. границею ф-ції f(x) у точці x = a, якщо.

. За Коші Число А називається границею ф-ції f(x) в точці А, якщо для будь-якого при якому: .

Границя при x до безк. Число А назив. гр. ф-ції f(x), при х до безк. Якщо для будь якого >0 існує таке число М залежне від і яке > 0, для будь якого x, x>M виконується р-сть .

1. 

2. Кінець однаковий |f(x)-A| <lim f(x)=A

10.Односторонні границі.

А назив. правосторонньою границею ф-ції f(x) при x прямує до а, якщо

А назив. лівосторонньою границею ф-ції f(x) при x прямує до а, якщо

Якщо ф-ція f(x) у точці x=a має границю, то існують лівосторонні і правосторонні границі у цій точці і вони рівні між собою.

11. Нескінченно малі і нескінченно великі.

Ф-ція назив. НВ при , якщо

Ф-ція назив. НВ при , якщо

Ф-ція назив. НМ при , якщо

Властивості НМ: 1. Скінчена сума НМ ф-цій при є НМ.

2. Добуток НМ на обмежену ф-цію є НМ.

3. Добуток скінченого числа НМ ф-цій є НМ.

4. Якщо f(x) – НМ, , то 1 / f(x) - НВ, .

12. Властивості гр. ф-ції у точці. Критерій існування ф-ції у т.

Нехай ф-ції f(x) і g(x) визначені околом точки а і існують границі і . Тоді існують і такі границі:

; ;

Критерій. Для того щоб існувала границя ф-ції f(x) в точці а необхідно і достатньо, щоб f(x)-A=d(x) була НМ, де .

Достатні умови існування ф-ції в точці.

1. Всяка обмежена і монотонна при ф-ція має границю в т. а

2. Якщо f(x), g(x), h(x) визначені в О(а) і Задовольняють в цьому околі ,

то .

x

. Доведення: Розгл. коло радіуса R.

S(три-ка OAC)<S(сектораOAC)<S(три-каOAB)

; ;

; ; ;

. Наслідки:

14. Друга чудова границя. Її наслідки.

Доведення.Нехай x>1, , тоді знайдеться n є N, що n x < n+1. N=[x]-ціла част. х.

1-й і 3-й вирази наближаються до e,n і до нескінченності. Отже і 2-й теж до e.

Наслідки:

15. Порівняння НМ.

НМ одного порядку малості позначають x(x)), x прямує до a.

, xє НМ більш високого порядку малості, ніж (x).

, навпаки.

. Еквівалентні.

16. Ланцюжок еквівалентності.

Теж саме з f(x) замість x. Теорема: у відношеннях та добутках НМ ф-цій під знаком lim можна змінювати на еквівалентні їм ф-ції.

Доведення:

;

Алгебраїчна сума НМ різного порядку малості еквівалентна НМ найменшого порядку малості.

17. Неперервність.

f(x) наз. неперервною у т. x₀ якщо:

1. Вона визначена у т. х. 2. Існує границя ф-ції у цій точці.

3. lim f(x)=f(x ₀) х прямує до х ₀.

За Коші. Ф-ція неперервна у т. х₀ якщо

f(x) назив. неперервною у т. х₀, якщо НМ приросту аргументу відповідає НМ приріст ф-ції.

f(x) наз. неперервною у т. х₀, якщо

18. Властивості неперервних.

Якщо f(x), g(x) – неперервні, то

. теж неперервні.

Якщо ф-ція x=t неперервна у т. t₀ ? а f(x) – неперервна у т. х₀=t то f((t)) тепер у т. t₀.

Теорема про неперервність оберненої ф-ції: y=f(x) неперервна у т. x₀ є x - числ. множина і надій множині існ. оберн. ф-ція x=f^-1(y) , то ця ф-ція є неперервною у т. y₀; y₀=f(x₀).

19. Точки розриву та їх класифікація.

Точки у яких ф-ція не існує або не визначена назив. точк. розриву.

1. . Розрив типу стрибка.

2. х₀ - т. усувного розриву.

3. Якщо одна з одностор. Границь не існує, або = нескінч. у т. х₀ , то х₀ – точка розриву 2-го порядку.

20. Функції неперервні на відрізку.

Ф-ція назив. неперервною на відрізку ab, якщо вона неперервна в кожній точці цього відрізку причому f(a+)=f(a), f(b-)=f(b).

1 теорема Вейерштрасса: Ф-ція неперервна на відрізку є обмеженою на цьому відрізку.

2 теорема Вейерштрасса:

Неперервна на відрізку ab ф-ція, набуває на цьому відрізку свого найбільшого значення.

1 теорема Бальцано-Коші: Якщо ф-ція неперервна на відрізку і на кінцях відрізка набуває протилежних знаків, то на відрізку існує хоча б 1 точка, в якій ф-ція вертається в “0”.

2 теорема Бальцано-Коші: Якщо ф-ція неперервна на відрізку і набуває на ньому свого max і min то вона набуває на відрізку і всі проміжні значення

21. Поняття похідної ф-ції.

Границя відношення приросту ф-ції до приросту аргументу, коли приріст аргументу прямує до нуля, назив. похідною ф-ції у т. х.

21-23. Похідна суми.

Похідна добутку.

Похідна частки.

24. Геометричний зміст похідної.

- р-ня дотичної у т. х₀.

Пряма перпендикулярна до дотичної у т. х₀ назив. нормаллю.

Економічний зміст похідної. Похідна – це швидкість зміни деякого екон. процесу. Якщо y=f(x) це ф-ція витрат залежна від х-кількості однорідної продукції, то похідна виражає граничні витрати виробництва. Коефіцієнт еластичності показує на скільки зміниться ф-ція при зміні аргумента на 1%. (при дослідж. попиту)

25. Необхідні умови існування похідної ф-ції у точці.

Ф-ція дифференційована у т. якщо в цій т. існує похідна, і недиференційована, якщо похідна не існує або = нескінч.

Якщо ф-ція диференційована у т. х₀, то вона неперервна у цій точці. Обернене твердження не вірне.

26. Похідна складеної і оберненої ф-цій.

Т1. Нехай ф-ція х=tдифер. у т. t, а ф-ція y=f(x) – диференційована у т. х₀=t₀, тоді ф-ція y=f((x)(t)) – дифер. у т.t₀.

Наслідок:

Т2. Якщо ф-ція y=f(x) дифер. у т. х₀ - дифер у т. y₀=f(x₀).

27. Похідні ф-цій, що задані неявно і параметрично.

Якщо ф-ція задана р-ням y=f(x) розв’язаним відносно y , то кажуть, що ф-ція задана явно. Якщо ф-ція задана р-ням F(x;y)=0 не розв. Відносно y , то кажуть, що ф-ція задана неявно. Щоб знайти похідну неявної ф-ції необхідно взяти похідну за змінною х від рівності F(x;y)=0 пам’ятаючи, що y – є ф-ція від х, а потім розв. р-ня відносно похідної y. Похідна буде виражаится через змінні х та y.

Якщо ф-ціональна залежність між х та y задається рівнянням:

, t – належить одному й тому ж проміжку, то кажуть що ф-ція задана параметрично. Якщо y=t строго монотонна, то існує обернена ф-ція і y можна записати у вигляді . Похідна: =

=

28. Логарифмічне диференціювання.

29. Правило Лопіталя.

Т1. Нехай ф-ції f(x), g(x) – дифер. в околі х₀. ,

у т. х₀ тоді якщо

то

Т2. Якщо ф-ція f(x), g(x) дифер. в околі т. х₀ і і то .

30. Поняття вищих порядків. Тейлор та Маклорен.

- друга похідна. Похідна від другої – третя..

Похідною n–го порядку ф-ції f(x) на інтервалі (a,b) назив. першу якщо вона існує від похідної n–го порядку. Похідні порядку вище першого назив. похідн. вищих або старших порядків.

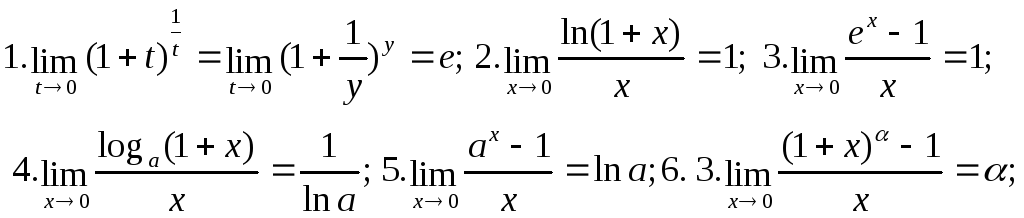
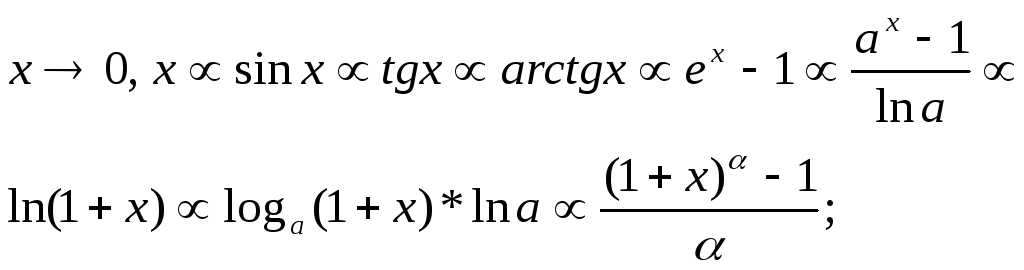
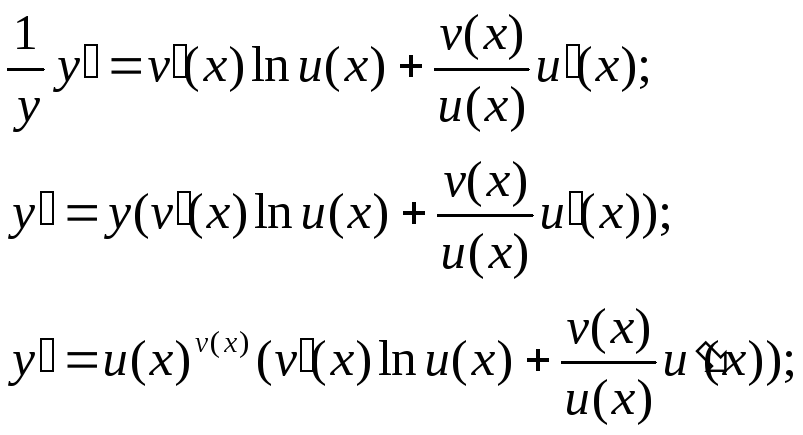
Ф-ла Тейлора. Нехай ф-ція дифер. в околі т. х₀ і має похідні (n+1)-порядку, x є околу т. х₀, тоді є така т. с що лежить між х і х₀ і ф-л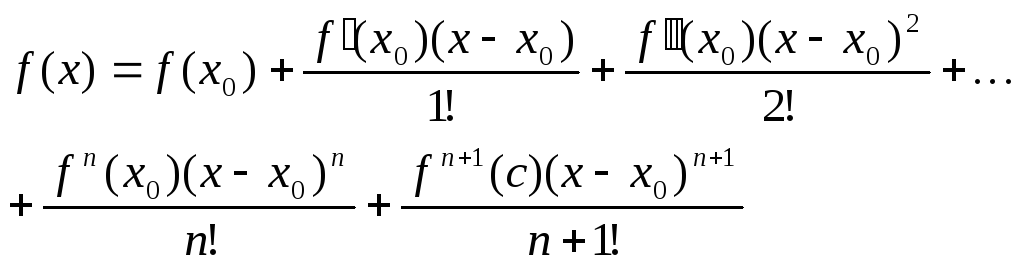а: Останній доданок – залишковий член, а все інше – “многочлен Тейлора”. При x₀ ф-ла назив. Маклорена.