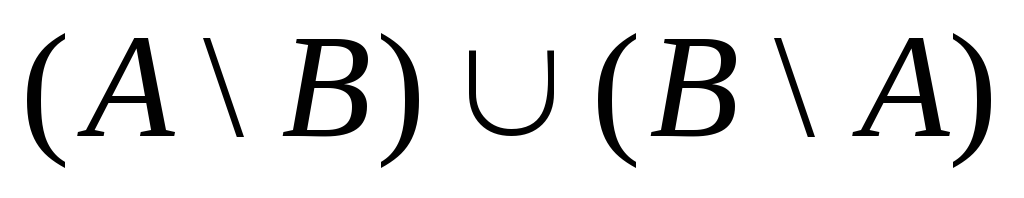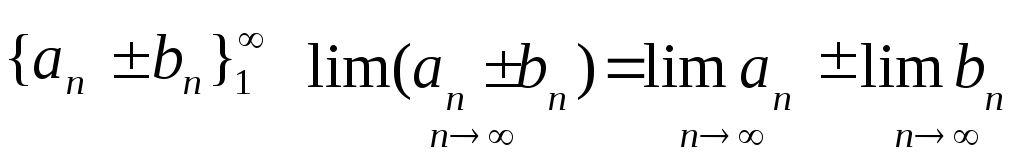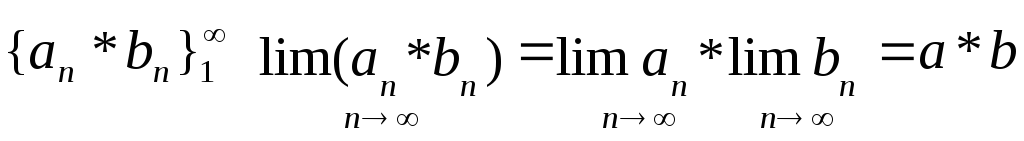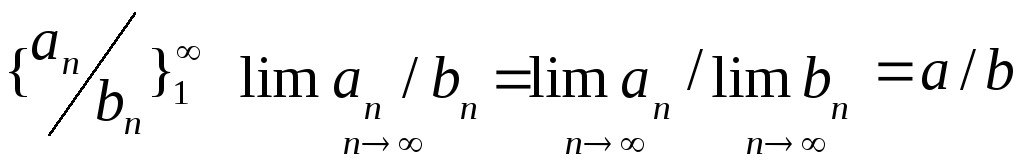shporapowushci
.doc|
1. Визначники другого та третього порядку їх властивості.
Детермінантом
або визначником другого порядку
квадратної матриці називають вираз
|
Визначник
3-го порядку Властивості.
|
|
2. Визначники n-ого порядку, означення. Властивості ті ж самі, що і в першому питанні. Визначники квадратної матриці, що складається з n^2 елементів, називається алгебраїчна сума n! доданків, кожен доданок є добутком n-доданків взятих по одному з кожного рядка і кожного стовпчика квадратної матриці і помножених на (-1)^t де t – це число інверсії в других індексах, якщо елементи доданку розташовані в порядку зростання перших індексів. 3. Обчислення визначників розкладом їх за елементами рядка чи стовпчика, теорема Лапласа.
Теорема Лапласа: Визначник n-го порядку дорівнює сумі добутків елементів деякого рядка (стовпчика) на їх алгебраїчні доповнення. Алгебраїчним доповненням Aij елемента aij називається мінор Mij взятий із знаком (-1)^i+j. |
4. Визначник розкладений за елементами рядка чи стовпчика та алгебраїчними доповненнями іншого рядка чи стовпчика.
5. Елементарні перетворення матриць. Застосування.
число. |
|
6. Зведення матриць до трапецієподібного вигляду за допомогою елементарних перетворень.
7. Ранг матриці та його властивості. Рангом матриці А називається найвищий порядок відмінного від нуля мінора цієї матриці.
r(A)=rank A= rang A Властивості.
|
8. Способи обчислення рангу матриці.
Вибираємо М2 , складаються мінори третього порядку , що місять цей мінор. Якщо всі мінори 3-го порядку = 0, тоді ранг = 2. Якщо хоча б один мінор 3-го порядку , повторюємо те саме.
Ранг трапецеподібної матриці = max числу її ненульових рядків. 9.Мінори матриці, базисний мінор. Мінор матриці, за розмірністю якого визначають ранг, називається базисним мінором. 10. Системи лінійних алгебраїчних рівнянь. Правило Крамера. n-рівнянь і m-невідомих. Система називається сумісною, якщо існують такі х1=в1, х2=в2, …, хм=вм,які при підстановці в систему задовольняють всі рівняння. Сукупність таких значень називають розв’язком системи. Однорідна система (всі частки системи дорівнюють 0) завжди сумісна.
|
|
Правило Крамера.
11. Метод Гаусса. Зводимо до трапецеподібної форми. Якщо потрібно, вводимо константи. Перетворюємо матрицю назад в систему. Обчислюємо систему. 12.Теорема Кронекера-Капеллі. Система однорідних рівнянь сумісна тоді і тільки тоді, коли ранг основної матриці системи = рангу розширеної. Система має єдиний розв’язок, якщо ранг = кількості невідомих і безліч, якщо ранг < кількості невідомих. |
13. Однорідні системи лінійних рівнянь. Критерій єдиності розв’язку. Однорідна система (всі частини системи дорівнюють 0) завжди сумісна.
Для того, щоб однорідна система мала ненульовий розв’язок необхідно і достатньо, щоб ранг матриці А < кількості невідомих, тоді цих розв’язків безліч. Якщо ранг (А) = кількості невідомих – матриця квадратна, визначник матриці коефіціентів , то однорідна система має єдиний розв’язок.
|
|
14.Операції над матрицями: транспонування, множення на число, додавання, властивості цих операцій. 1. Додавання.
Властивості: - А + В = В + А комутативна
2. Множення на дійсне число. Властивості: дистрибутивні (А+В)=А+В; ()А=А+А; асоціативна (А= (А); 3. Транспонування Заміна рядків стовпчиками, а стовпчики рядками.
|
15.Множення матриць, властивості добутку матриць.
Властивості: А(В+С)=АВ+АС; (А+В)С=АС+ВС; (АВ)С=А(ВС) 16. з 9 і 17.
|
|
17. Обернені матриці. Правило обчислення і властивості обернених матриць. Якщо А – квадратна матриця, то матриця А^-1 називається оберненою до А, якщо А^-1*A=A*A^-1=E. Щоб квадратна матриця А мала обернену необхідно і достатньо, щоб вона була невиродженою, тобто щоб її визначник не дорівнював 0.
Властивості оберн. матриць:
|
18. Власні числа та власні вектори матриць. Ненульовий вектор х такий, що АХ=Х, називають власним вектором матриці А. Число назив. власним числом матриці А.
Система має ненульовий розв’язок коли визначник дорівнює 0. Розкриваючи визначник отримаємо рівняння n-го степеня відносно . Розв’язуючи це рівняння знаходимо власні числа матриці А. Для кожного знаходять власний вектор. |
|
19. Вектори на площині і у просторі. Основні поняття. Геометричним вектором називається напрямлений відрізок прямої. Довжину цього відрізка називають модулем або довжиною вектора. Задати вектор означає вказати його довжину і напрям. Вектор довжина якого дорівнює нулю називається нуль-вектором. Напрям нуль-вектора не заданий. Вектори назив. рівними, якщо вони мають однакову довжину і напрям. Вектор довжина якого = 1 назив. одиничним. Одиничний вектор співнапрямлений вектору а назив. ортом. Оскільки геометричні вектори можна переміщувати по площині, то їх називають вільними. Кутом між векторами а і b зведеними до спільного початку назив. найменший кут на який треба повернути вектор a , щоб напрями a і b співпали. Поворот проти годинникової стрілки вважається додатнім. Кути між вектором та координатними осями Ох та Оу назив. напрямленими, а cos цих кутів напрямленими косинусами. На площині напрямлені cos пов’язані співвідношенням cos^2+cos^2=1. |
20. Вектори на площині і лінійні операції над векторами, їх властивості. 1. Добутком дійсного числа на вектор назив. новий вектор довжина якого дорівнює довжині вектора помноженого на модуль числа , а напрямок співпадає з напрямком вектора , якщо >0, і протилежно напрямлений, якщо <0. 2. Сумою векторів називають такий вектор c, у якого початок співпадає з початком вектора , а кінець співпадає з кінцем вектора , за умови, що початок вектора співпадає з кінцем вектора Різницею назив. такий вектор c, напрямлений з кінця вектора в кінець вектора , за умови, що початки векторів і співпадають.
Властивості:
|
|
Координати кінця вектора називають координатами вектора. Позначимо через i одиничний вектор, напрям якого співпадає з віссю Ох. Через j одиничний вектор напрям якого співпадає з віссю Оу.
Якщо відомо координати початку А=(Х1;У1) і кінця В=(Х2;У2), то АВ=(Х2-Х1; У2-У1). 22. Проекція вектора на вісь, вектор на вектор. Проекцією вектора АВ на вісь t називається число, що дорівнює довжині відрізка А1В1 взятий зі знаком + якщо кут між вектором АВ і t гострий, і зі знаком – якщо цей кут тупий.
A1 ) B1 |
Проекцією вектора a на вектор b називається проекція вектора a навісь напрям якої збігається з напрямом вектора b. Властивості проекцій : 1. Проекція сум скінченного числа векторів на вісь t дорівнює сумі проекцій кожного з векторів на цю вісь
2. Проекція вектора помноженого на ненульове число лямбда дорівнює добутку цього числа лямбда на проекцію вектора.
23. Умови колінеарності та компланарності. Вектори
a і b називаються колінеарними,
якщо вони лежать на одній або паралельних
прямих.
Три вектори a, b, c називаються компланарними, якщо вони лежать в одній або паралельних площинах, зокрема якщо хоча б 2 із 3-ох векторів колінеарні, або хоча 1 є нуль-вектором.
|
|
24. Скалярний добуток векторів, його властивості. Скалярним добутком векторів a і b називають число, що дорівнює добутку модулів a і b на косинус кута між ними.
Властивості:
Вектори a і b перпендикулярні тоді, коли їх скалярний добуток дорівнює 0. Якщо хоча б один з векторів є нуль-вектором, то скалярний добуток = 0.
|
25. Базис у R^2. Ортонормований базис. Будь-яка пара впорядкованих неколінеарних векторів утворює R^2 базис. i,j – ортонормований базис. Нехай a=(Xa,Ya) b=(Xb,Yb), то ці вектори будуть утворювати базис за умови Xa/XbYa/Yb. Теорема: Якщо вектори E1 та E2 утворюють базис R^2, то будь-який третій вектор можна подати у вигляді лінійної комбінації двох перших векторів. a=X1E1+X2E2 a(X1, X2) Таке представлення вектора а називається розкладом його за базисом E1 та E2. Теорема2. Розклад за базисом єдиний
26.Базис R^3. Базисом R^3 наз. будь-яка впорядкована трійка некомпланарних векторів. Базис i,j,k – ортонормований. Теорема: Якщо вектори E1 , E2, E3 утворюють базис, то будь-який четвертий вектор а можна подати у вигляді лінійних комбінацій цих векторів. a=X1E1+X2E2+X3E3 a(X1, X2, X3) |
|
27. Обчислення скалярного добутку векторів, які задані своїми координатами. Якщо вектори задані своїми координатами, то скалярний добуток дорівнює сумі добутків відповідних координат. 28. Прямі на площині та їх рівняння. Рівняння прямої, що проходить через дві задані точки.
Рівняння з кутовим коефіцієнтом:
Канонічне рівняння прямої: Параметричні рівняння прямої:
Кут
між прямими:
|
29. Площини та прямі в R^3, їх рівняння. Рівняння площини, що проходить через 3 задані точки.
Потрібно знайти детермінант. Вийде р-ня вигляду ax+by+cz+d=0 Рівняння площини, що проходить через точку перпендикулярно до заданого вектора
Пряму у просторі можна задати як перетин 2 площин.
|
|
Лінії, які задаються р-ням 2-го степеня відносно Х та У називаються кривими 2-го порядку.
Еліпсом наз. геометричне місце точок, сума відстаней яких від двох даних точок (фокусів) є величина стала.
Канонічне
р-ня еліпса:
Графік еліпса: d B2 d
A1 A2 F1 F2
B1 |
Гіперболою назив. геометричне місце точок, різниця відстаней яких від двох даних точок є величина стала.
Канонічне
р-ня гіперболи:
Графік: l2 d d l1
B2
F1 F2 -a a A1 A2
B1
|
|
Канонічне
рівняння параболи:
Графік:
NM=MF Y1^2=2p1x Y2^2=2p2x
N M
0 F Y1 P
Y2 |
|
A={a;b;c;…} Множина A скл. З елементів a,b,c,… Для
задання конкретної множини необхідно
чітко описати ті елементи, які належать
цій множині.
Множини
назив. рівними якщо вони скл. з
однакових елементів. Якщо множина А
скл. з всіх тих елементів множини В,
які мають визначену властивість, то
пишуть
2. Об’єднання та перетин множин, їх властивості. Для
двох будь-яких множин А,В множина, що
скл. з тих і тільки тих елементів, які
належать хоча б одній з множин А,В,
назив. об’єднанням множин А і В і
позначається
Для
двох будь-яких множин А,В множина, що
скл. з тих і тільки тих елементів, які
належать і А, і В, навзив. перетином
множин А і В і познач.
|
Для будь-яких двох множин А і В множина всіх елементів В, що не належать множ. А, назив. різницею множ. А і В і познач. B\A.
Якщо множина А явл. підмножиною В, то В\А назив. доповненням А в В.
3. Відображення множин, поняття функції. Якщо для кожного x є X за визначеним правилом вибраний елемент y є Y, то кажуть, що задана функція(відображення) f множини X в множину Y, при цьому пишуть f: XY. Елемент х є Х назив. аргументом функції, елемент у є Y – значенням функції, відповідним елементу х є Х, y = f(x), а сама ф-ція є правилом, що перероблює кожний х є Х в y = f(x). Множина Х назив. областю визначення ф-ції, а множина всіх елементів у є Y, для яких існують х є Х такі, що f(x) = y – множиною значень ф-ції f. |
|
4. Поняття числової послідовності, способи задання. Нескінченною
числовою послідовністю наз. відображення
множини N у множ. R.
Числа an наз. елементами числової послідовності. n – номер елемента. Числову послідовність можна задати точками на числовій прямій або точками на площині. Послідовність вважається заданою, якщо відомо правило знаходження її n-го члена. Якщо відомо номер члена, то можна знайти і сам елемент. Найчастіше послідовність задають формулою її n-го члена. Інколи задається рекурентна формула n-го члена, тобто задаються перші кілька елементів, а потім формула для знаходження наступних елементів через попередні. Іноді числові послідовності записуються словами. 5. Сталі, монотонні, обмежені послідовності. Їх границі.
Числова послідовність
|
Числова
послід. назив. зростаючою, якщо
Чис.
посл. наз. не спадною, якщо
Число
а наз. границею послідовності
|
|
6. Властивості збіжних послідовностей. Теорема про суму збіжних послідовностей. Послідовність, що має скінчену границю назив. збіжною. Якщо границя не існує або нескінченна, послідовність назив. розбіжною.
Нехай
послід.
1. |
Оскільки
|

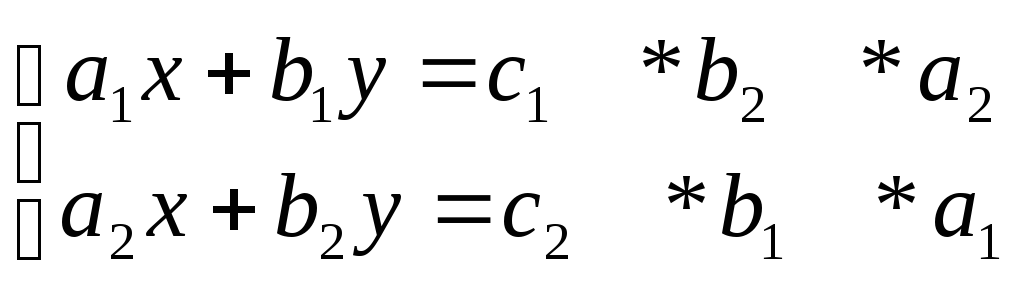
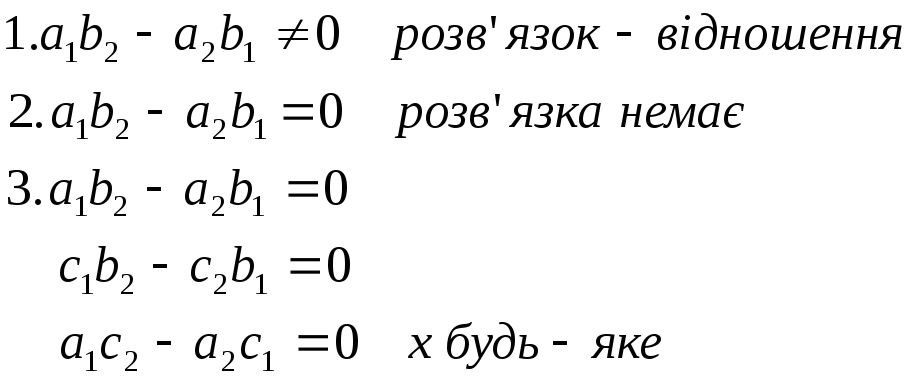
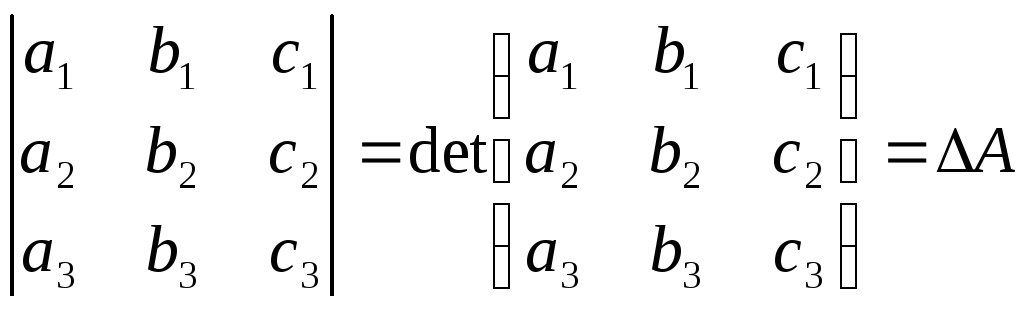
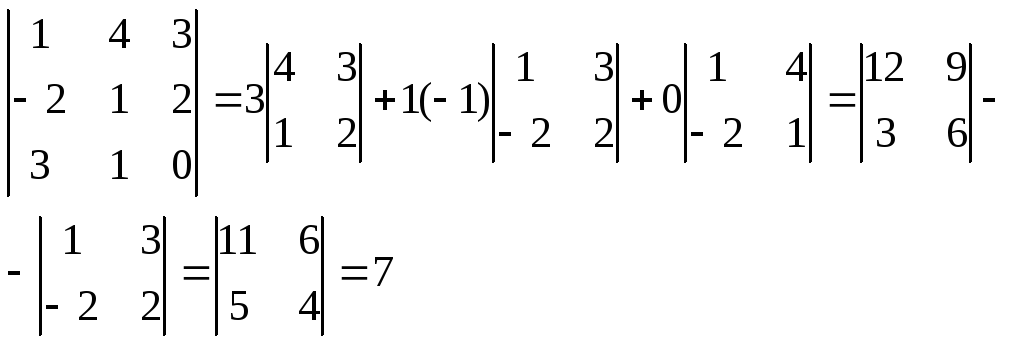
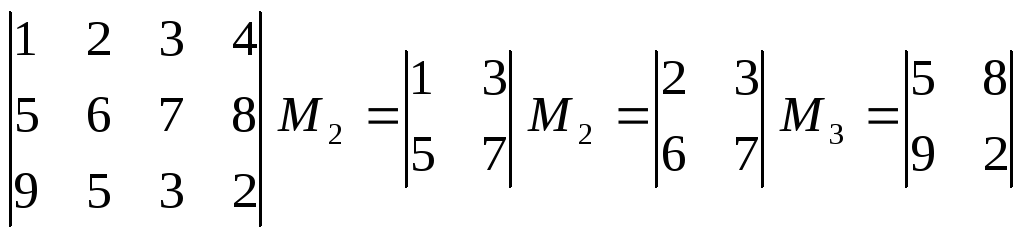
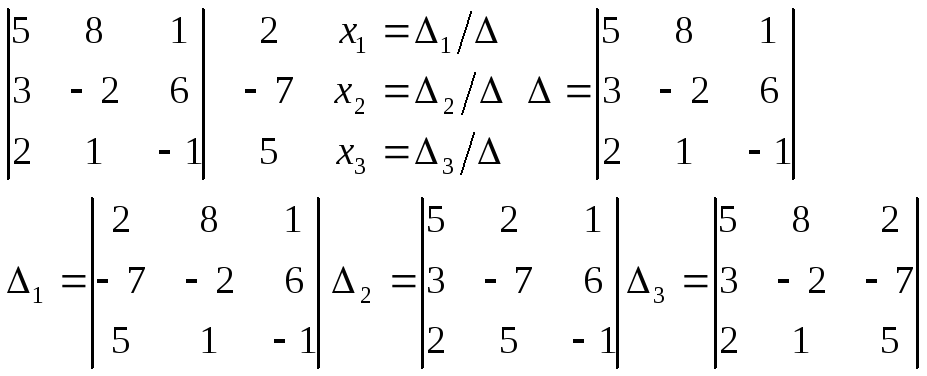
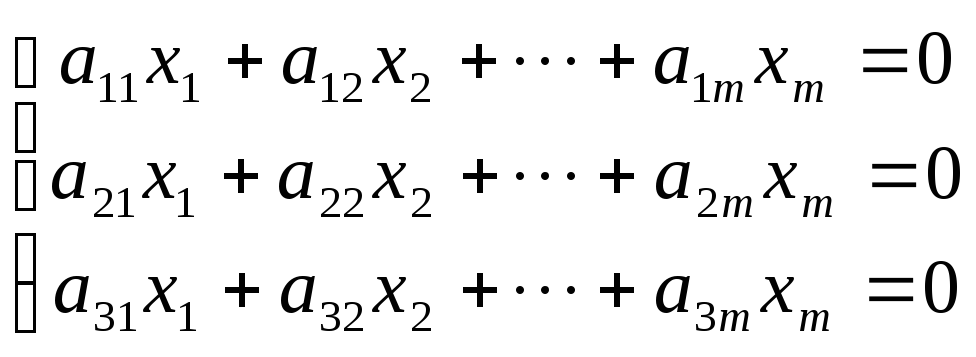
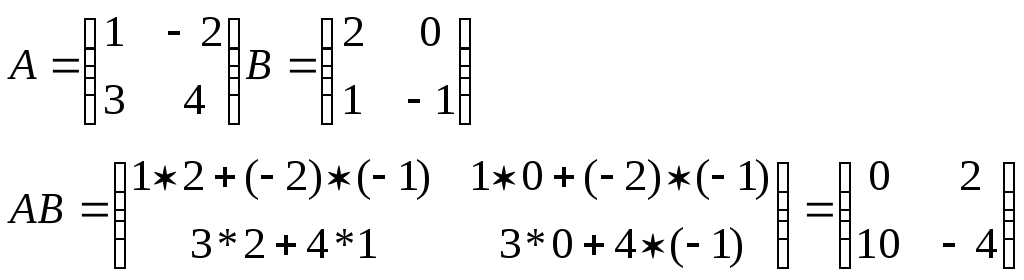
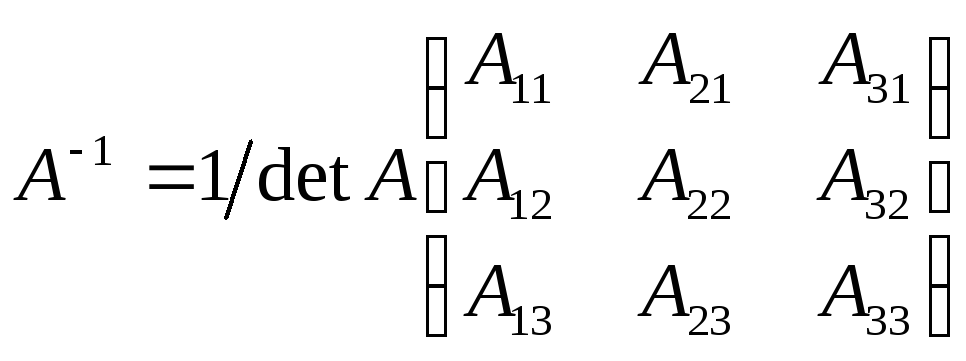
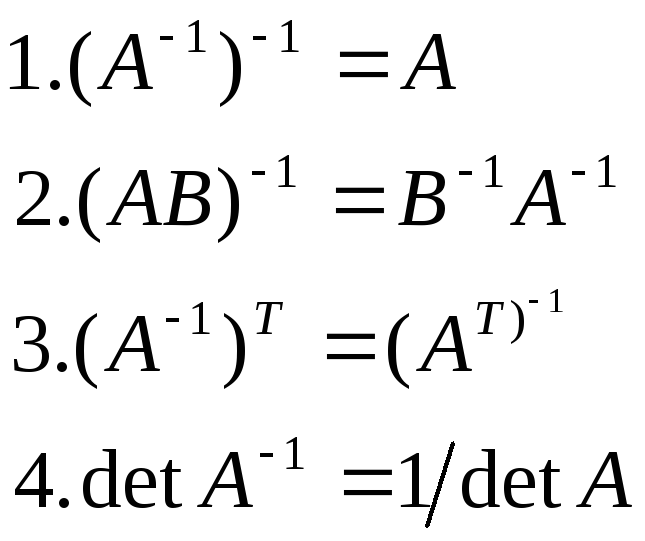
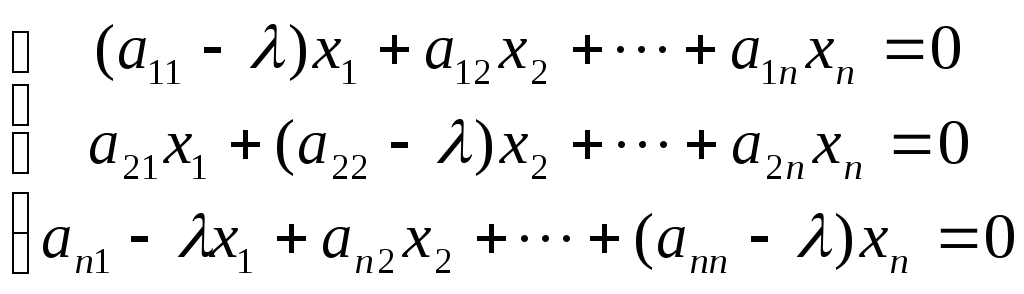
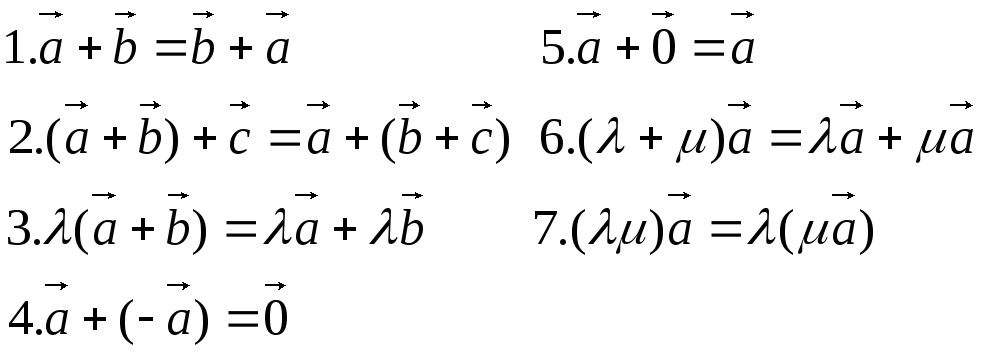


 21.
Координати вектора. Лінійні операції
над векторами у координатній формі.
21.
Координати вектора. Лінійні операції
над векторами у координатній формі.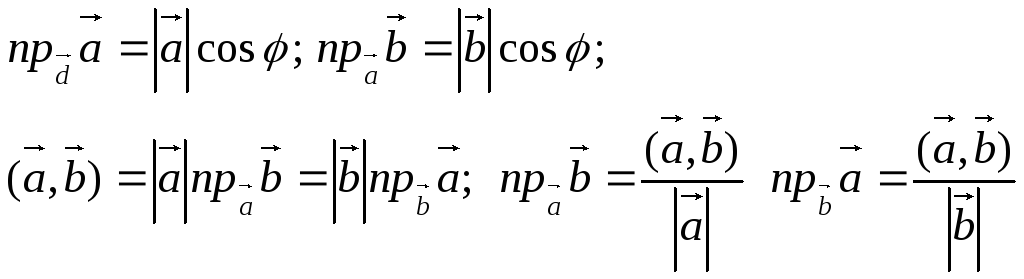
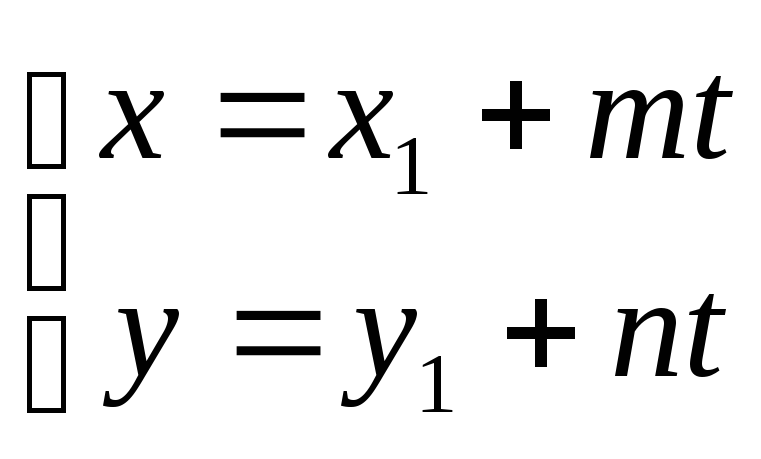
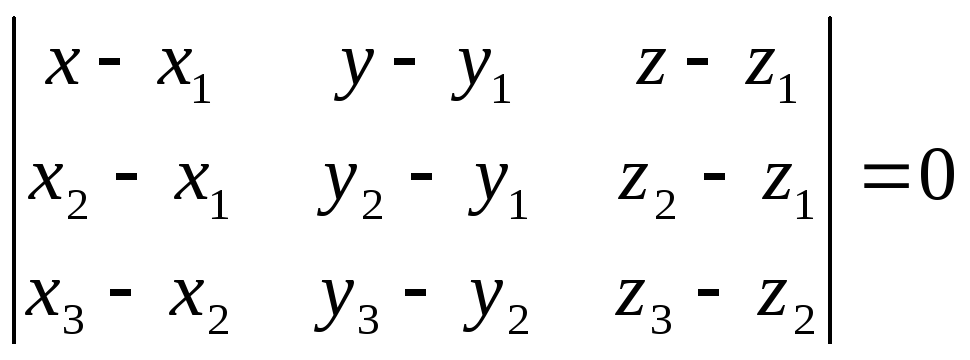
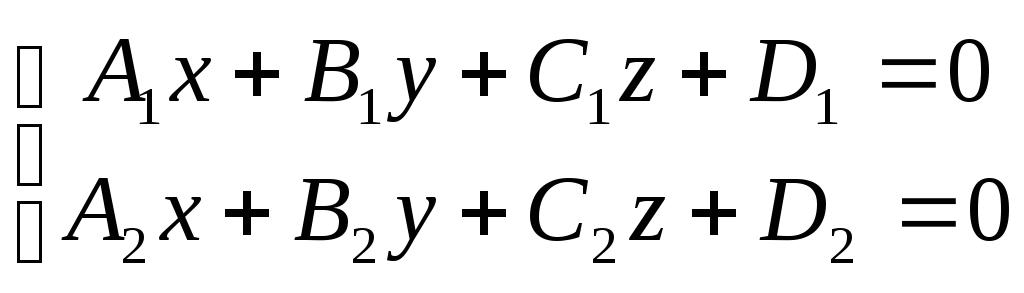

















 30.
Криві другого порядку, їхнє значення,
графіки і канонічні рівняння. (еліпс,
гіпербола, парабола).
30.
Криві другого порядку, їхнє значення,
графіки і канонічні рівняння. (еліпс,
гіпербола, парабола).





 Параболою
наз.
геометричне місце точок, рівновіддаленої
від даної точки і даної прямої
(директрис).
Параболою
наз.
геометричне місце точок, рівновіддаленої
від даної точки і даної прямої
(директрис).