3. Розрахунок міцності похилих перерізів

Розрахунок міцності похилих перерізів виконується в тій же послідовності, за тими ж формулами, що й в другорядній балці (15, с. 678).

Армування панелі виконати зварними каркасами і сітками.

Приклади розрахунку і конструювання ребристої панелі за першою групою граничних станів наведені в (15, с. 647-651).

3. Розрахунок панелі за другою групою граничних станів

1. Розрахунок панелі за деформаціями.

Відповідно до (9, п. 1.20) прогини елементів залізобетонних конструкцій не повинні перевищувати допустимих значень з урахуванням естетичних вимог. Розрахунок прогинів у цьому випадку повинен бути орієнтований на дію постійних і довготривалих навантажень, які беруться за (2, п.7) з коефіцієнтом надійності за навантаженням, що дорівнює одиниці.

Для окремих виробничих будівель, для яких прогини панелей перекриття обмежуються технологічними вимогами, розрахунок проводиться на дію постійних, тривалих і короткодіючих навантажень.

Поперечний переріз панелі приводиться до еквівалентного двотаврового або таврового перерізу.

Згідно з (9, п. 1.16 і табл.. 2) до панелей, що проектуються, ставляться вимоги третьої категорії тріщиностійкості, стосовно яких допускається обмеження по ширині, короткочасне і тривале розкриття тріщин.

Для елементів залізобетонних конструкцій, для яких допускається утворення тріщин, нормальних до повздовжньої осі елементів, прогини визначаються за кривизнами осі елемента, який згинається (9, пп.. 4.27-4.36).

Для елементів прямокутного, таврового та двотаврового перерізу кривизна визначається за формулою (170) в (9).

,

де - початкова кривизна від короткочасної дії всього навантаження;

- початкова кривизна від короткочасної дії тривало діючого навантаження;

- повна кривизна від тривало діючої частини навантаження.

Значення кривизни ;;визначаються за формулою

.

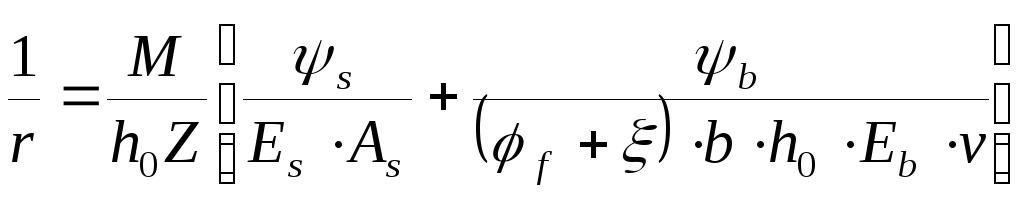Розрахунок панелі перекриття за деформаціями рекомендується виконувати в такій послідовності:

1. Визначаємо коефіцієнт пружності . Його значення для важкого бетону беремо:

а) при тривалій дії навантаження - = 0,10 сухий режим роботи будівлі≤ 40%;= 0,15 нормальний режим роботи> 40%;

б) при короткочасному навантаженні = 0,45.

2. Визначається коефіцієнт 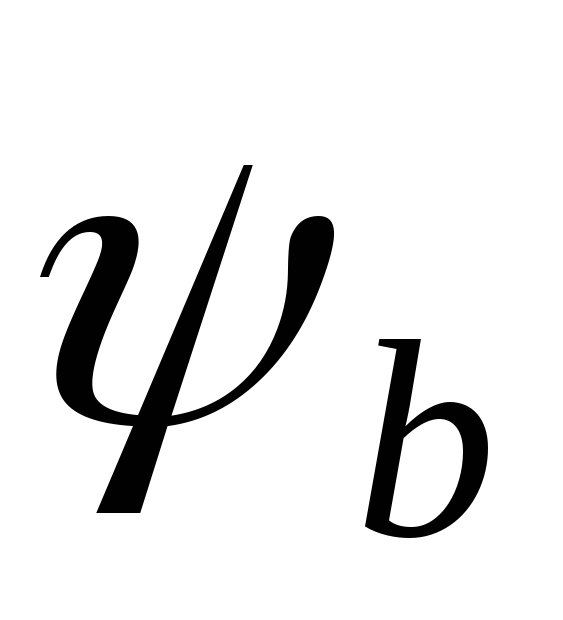, що враховує нерівномірність розподілу деформацій крайнього стиснутого волокна за довжиною ділянки з тріщинами і береться рівним для важкого бетону= 0,9.

3. Вираховуємо модульне відношення :

.

4. Знаходимо коефіцієнт армування :

.

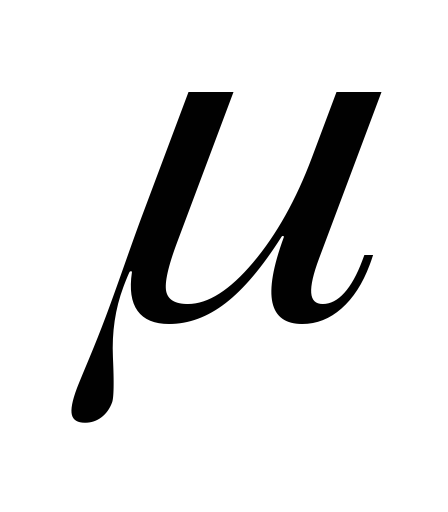5. Вираховуємо значення коефіцієнта:

.

Для перерізу у вигляді тавра полицею вниз і прямокутного = 0.

6. Визначаємо значення коефіцієнта відносної несучої здатності :

.

7. Знаходимо значення коефіцієнта :

.

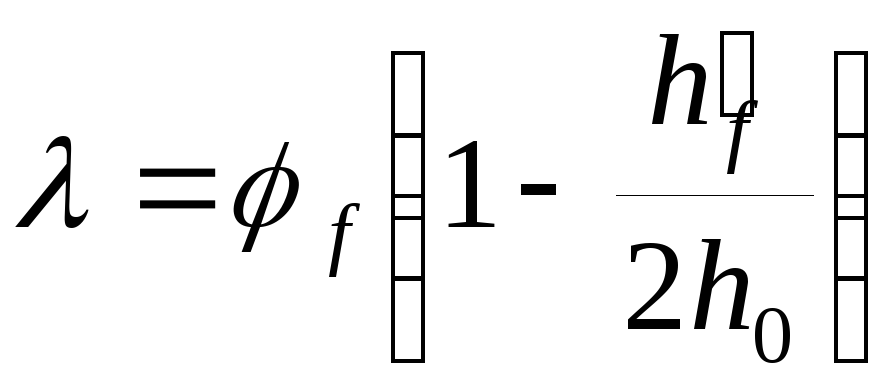Для перерізу у вигляді тавра полицею донизу і прямокутника значення = 0.

8. Вираховуємо відносну висоту стиснутої зони бетону:

.

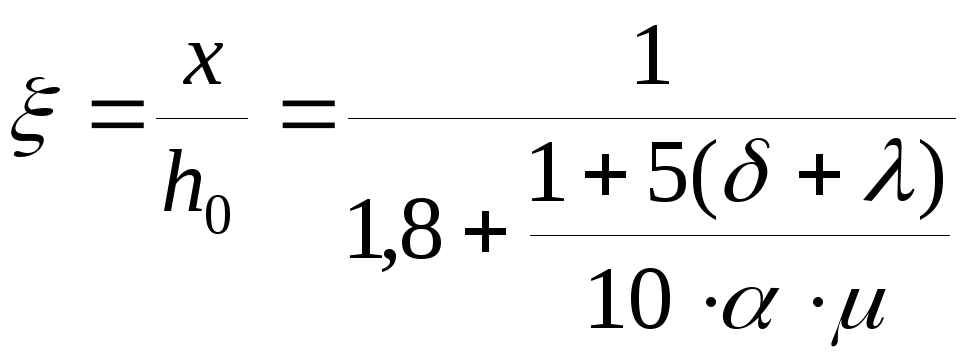Примітка. Якщо для тавра полицею догори або двотавра виявиться, що нейтральна вісь проходить у полиці, а саме , то необхідно виконати перерахунокяк для прямокутного перерізу шириною, попередньо визначивши значеннята, а саме пп. 4.6 даного алгоритму при.

9. Визначаємо плече внутрішньої пари сил:

.

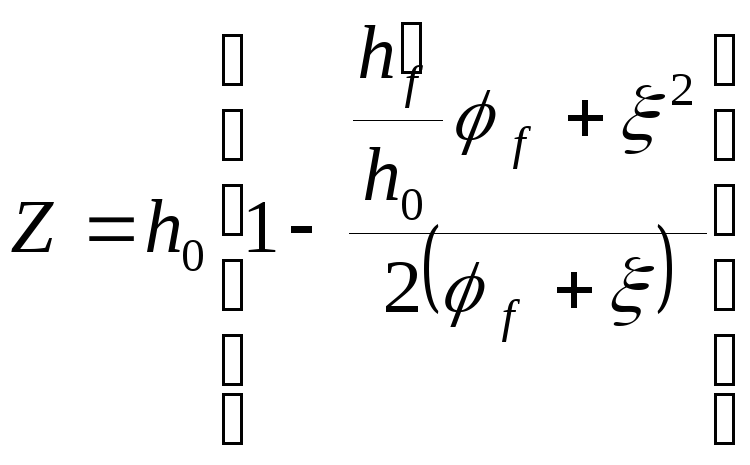Для прямокутного перерізу значення має вигляд

10. Знаходимо пружний момент опору 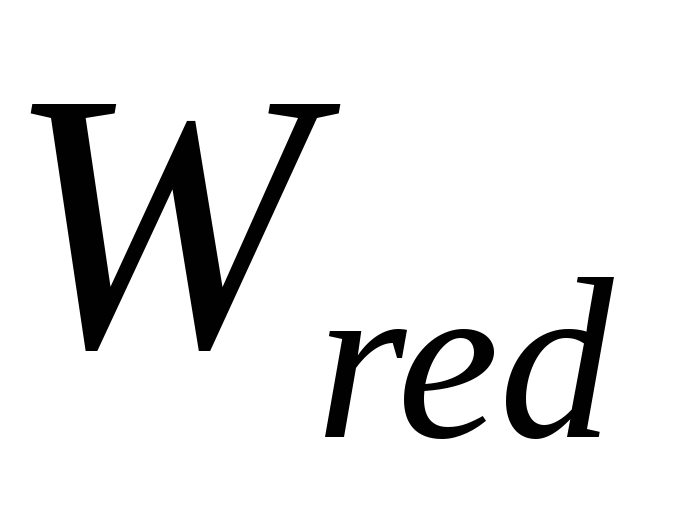по крайній розтягнутій зоні

,

де - момент інерції перерізу відносного центра ваги перерізу;

- відстань від центра ваги перерізу до крайнього розтягнутого волокна.

11. Вираховуємо пружнопластичний момент опору по розтягнутій зоні:

,

де - коефіцієнт, який береться рівним для прямокутного перерізу 1,75, для таврового – 1,5.

12. Визначаємо значення коефіцієнта , що враховує вплив дії навантаження за (9, п. 4.29). Тут= 1,1 – при короткочасній дії навантаження для арматури періодичного профілю;= 1,0 – при короткочасній дії навантаження для гладкої арматури;= 0,8 – при тривалій дії навантаження незалежно від профілю арматури.

13. Знаходимо коефіцієнт, що враховує роботу розтягнутого бетону на ділянці з тріщинами

14. Вираховуємо значення кривизни , і прогин. Для двохопорної балки, завантаженої рівномірно розподіленим навантаженням із шарнірним опиранням,=5/48.

15. Визначаємо значення і:

;

,

де - відповідно момент від тривало діючої частини навантаження;

- момент від повного навантаження.

16. Визначаємо значення (для цього необхідно виконати всі 14 попередніх пунктів, тому що міняються коефіцієнти)і. Завизначають прогин:

.

17. Значення повного прогину:

.

18. Знаходимо значення відносного прогину і порівнюємо з допусковими (9, с. 5):

.