
- •Розділ 1. Предмет, особливості та сфери застосування математичного програмування в економіці. Класифікація задач
- •1.1. Предмет курсу «математичне програмування»
- •1.2. Найпростіша класифікація задач математичного програмування
- •1.3. Програма дисципліни «Оптимізаційні методи та моделі»
- •Тема 9. Задачі динамічного програмування
- •Тема 10. Моделі та методи стохастичного програмування
- •Тема 11. Елементи теорії ігор
- •Розділ 2. Загальна задача лінійного програмування та методи її розв’язування
- •2.1. Загальна математична модель лінійного програмування
- •2.2. Форми запису задач лп
- •2.3. Геометрична інтерпретація злп
- •2.4. Основні аналітичні властивості розв’язків задач лінійного програмування
- •2.5. Графічний метод розв’язування задач лінійного програмування
- •2.5.1. Основи графічного методу
- •2.5.2. Навчальні завдання. Розв’язування задач графічним методом
- •2.6. Симплексний метод розв’язування задач лп
- •2.6.1. Теоретичні відомості
- •2.6.2. Навчальні завдання розв’язування задач симплекс-методом
- •Розділ 3. Двоїстість у лінійному програмуванні
- •3.1. Поняття двоїстості. Правила побудови двоїстих задач
- •3.2. Теорема двоїстості
- •3.3. Навчальні завдання
- •Розділ 4. Економічна інтерпретація двоїстих задач. Аналіз оптимальних планів лінійних економіко-математичних моделей
- •4.1. Економічна інтерпретація двоїстої задачі
- •4.2. Навчальні завдання
- •Розділ 5. Транспортна задача
- •5.1. Постановка транспортної задачі
- •5.2. Метод потенціалів
- •5.3. Навчальні завдання
- •Розділ 6. Вибрані розділи математичного програмування
- •6.1. Цілочислове програмування
- •6.1.1. Постановка задачі
- •6.1.2. Метод Гоморі
- •6.1.3. Метод «віток і меж»
- •6.1.4. Приклади цілочислових економічних задач
- •6.2. Дробово-лінійне програмування
- •6.2.1. Постановка задачі та алгоритм розв’язування
- •6.2.2. Приклади дробово-лінійних задач
- •6.3. Нелінійне програмування
- •6.3.1. Постановка задачі
- •6.3.2. Труднощі розв’язування задач нелінійного програмування
- •6.3.3. Метод множників Лагранжа
- •6.3.4. Приклади задач нелінійного програмування
- •6.4. Динамічне програмування
- •6.4.1. Сутність динамічного програмування. Принципи оптимальності
- •6.4.2.Методикарозв’язування динамічних задач
- •6.4.3. Приклади розв’язування динамічних задач
- •6.5 Теорія ігор
- •6.5.1. Основні поняття теорії ігор
- •6.5.2. Зведення матричної гри до задачі лінійного програмування
- •6.6. Стохастичне програмування
- •6.6.1 Постановка задач і методи розв’язування
- •6.6.2. Приклади стохастичних економічних задач
6.1.3. Метод «віток і меж»
Ефективнішим за метод Гоморі розв’язування задач цілочислового програмування є метод «віток і меж». Спочатку, як і в разі методу Гоморі, розв’язується послаблена (відкиданням умови цілочисловості) задача.
З цією метою застосовується симплексний метод.
Нехай
потрібно знайти хj
— цілочислову змінну, значення якої
![]() в оптимальному плані послабленої задачі
є дробовим. Тоді можна стверджувати, що
в інтервалі
в оптимальному плані послабленої задачі
є дробовим. Тоді можна стверджувати, що
в інтервалі![]() цілих значень немає.
цілих значень немає.
Наприклад,
якщо
![]() дістаємо інтервал (2,3), де, очевидно,
немаєхj,
яке набуває цілого значення.
дістаємо інтервал (2,3), де, очевидно,
немаєхj,
яке набуває цілого значення.
Значенню
![]() відповідає інтервал (–3; –2), де також
не існує цілого значенняхj.
Отже, допустиме ціле значення xj
має задовольняти одну з нерівностей
відповідає інтервал (–3; –2), де також
не існує цілого значенняхj.
Отже, допустиме ціле значення xj
має задовольняти одну з нерівностей
![]() або
або
![]() .
.
Приписавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві не пов’язані між собою задачі. Тобто початкову задачу цілочислового програмування (6.1)—(6.4) розіб’ємо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими. Це означає, що симплекс-методом розв’язуватимемо дві такі задачі:
![]() (6.5)
(6.5)
за умов
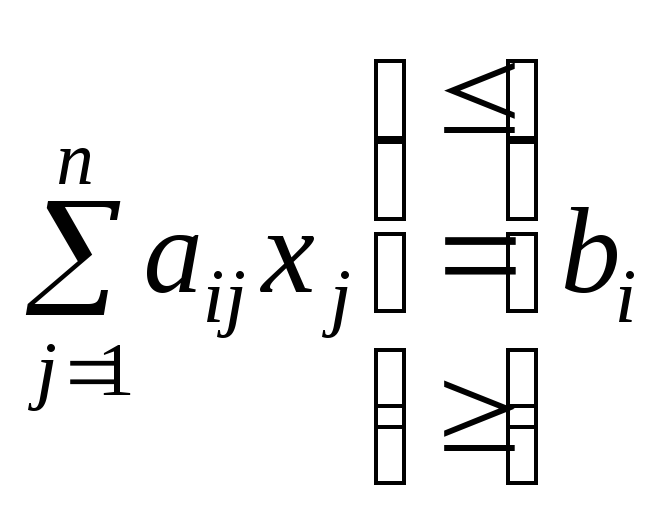 (6.6)
(6.6)
![]() ,
,
![]()
![]() ,
(6.7)
,
(6.7)
![]() — цілі, (6.8)
— цілі, (6.8)
![]() ;
(6.9)
;
(6.9)
![]() (6.10)
(6.10)
за умов
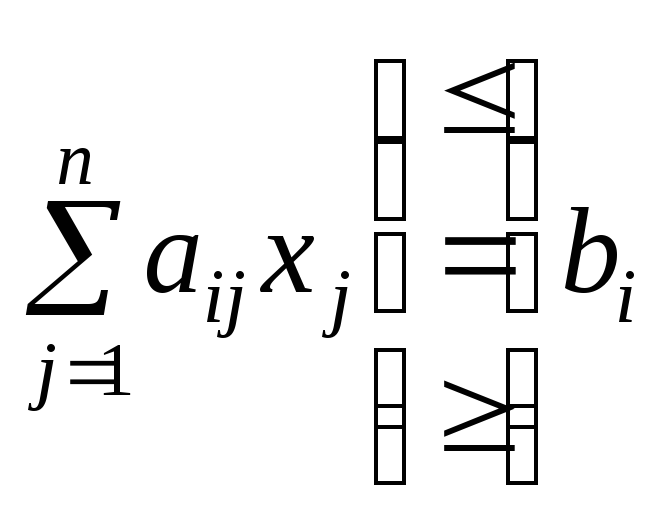 (6.11)
(6.11)
![]() ,
,
![]()
![]() , (6.12)
, (6.12)
![]() — цілі,
— цілі,![]() (6.13)
(6.13)
![]() ,
(6.14)
,
(6.14)
де
![]() — компонент розв’язку задачі (6.1)—(6.4).
— компонент розв’язку задачі (6.1)—(6.4).
Далі симплекс-методом розв’язуємо послаблені задачі (6.6)—(6.9) і (6.10)—(6.14), тобто з відкиданням обмежень (6.8) і (6.13). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв’язками задачі (6.1)—(6.4). Інакше пошук розв’язку задачі триває. Для подальшого розгалуження беремо задачу з найбільшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з найменшим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв’язку. Здобутий план — оптимальний.
Розв’язування цілочислових задач методом «віток і меж» можна значно прискорити, приєднавши обмеження виду (6.9) і (6.14) до останньої симплекс-таблиці не початкової (6.1)—(6.4), а відповідних задач.
Розв’яжемо методом «віток і меж» задачу 6.1.
Відкинувши
умову цілочисловості, дістанемо розв’язок
х1 = 1,
х2 = ![]() .
Отже, допустиме ціле значеннях2
має задовольняти одну з нерівностей
.
Отже, допустиме ціле значеннях2
має задовольняти одну з нерівностей
![]() або
або![]() .
Далі приєднуємо до задачі кожне з
обмежень, нехтуючи умовою цілочисловості,
і розв’язуємо по черзі обидві утворені
задачі. Для першої (з обмеженням
.
Далі приєднуємо до задачі кожне з
обмежень, нехтуючи умовою цілочисловості,
і розв’язуємо по черзі обидві утворені
задачі. Для першої (з обмеженням![]() )
оптимальним буде розв’язок
)
оптимальним буде розв’язок![]() ,
,![]() ,
,![]() ,
а для другої (з обмеженням
,
а для другої (з обмеженням![]() )
— розв’язок
)
— розв’язок![]() ,
,![]() ,
,![]() .
Оскільки цілочислового плану не знайдено,
процес необхідно продовжити, узявши
для наступного розгалуження першу
задачу, оптимальний план якої дає більше
значення функціоналу. Далі розв’язуємо
задачу, приєднуючи до неї обмеження
.
Оскільки цілочислового плану не знайдено,
процес необхідно продовжити, узявши
для наступного розгалуження першу
задачу, оптимальний план якої дає більше
значення функціоналу. Далі розв’язуємо
задачу, приєднуючи до неї обмеження![]() і
і![]() ,
звідки й знаходимо оптимальний план
,
звідки й знаходимо оптимальний план
![]() ,
,![]() ,
що збігається з розв’язком, здобутим
за методом Гоморі.
,
що збігається з розв’язком, здобутим
за методом Гоморі.
6.1.4. Приклади цілочислових економічних задач
Задача 6.2.
Побудувати загальну і числову модель лінійного розкрою. За критерій оптимізації є сенс узяти мінімум відходів.
Розв’язування.
Нехай
![]() — вид заготівки. Кожний прут можна
розрізати різними
— вид заготівки. Кожний прут можна
розрізати різними![]() способами.
способами.
Скористаємося такими позначеннями:
![]() —вихід
заготовок і-го
виду в разі розрізування прута j-м
способом;
—вихід
заготовок і-го
виду в разі розрізування прута j-м
способом;
cj — відходи в разі розрізування прута j-м способом;
А— кількість наявних прутів;
Bi, Di — відповідно нижня і верхня межі потреби в і-й заготівці;
xj — кількість прутів, які розрізані за j-м варіантом.
Запишемо загальну економіко-математичну модель лінійного розкрою.
Критерій оптимальності:
![]()
за умов
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() —цілі
—цілі
![]() .
.
Побудуємо числову економіко-математичну модель розрізування прутів, розглянувши можливі варіанти такого розрізування:
|
Довжина заготівки, м |
Варіанти розрізування прутів | ||||||
|
|
|
|
|
|
|
| |
|
1,4 |
4 |
— |
— |
1 |
1 |
2 |
2 |
|
2 |
— |
3 |
— |
1 |
2 |
1 |
— |
|
2,5 |
— |
— |
2 |
1 |
— |
1 |
1 |
|
Довжина відходів, м |
0,4 |
0 |
1 |
0,1 |
0,6 |
1,2 |
0,7 |
Бажано, щоб у множину ввійшли всі можливі варіанти, навіть такі, які на перший погляд здаються неефективними, наприклад x6.
Запишемо числову економіко-математичну модель розрізування прутів:
![]()
за умов
а) щодо кількості заготівок завдовжки 1,4 м:
![]() ;
;
2 м:
![]() ;
;
2,5 м:
![]() ;
;
б) щодо кількості наявних прутів:
![]() ;
;
в) щодо невід’ємності змінних:
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
г) щодо цілочисловості змінних:
![]() —цілі числа.
—цілі числа.
Пропонуємо розв’язати цю задачу одним із методів цілочислового програмування.
Задача 6.3.

Рис. 6.2
Записати загальну і числову економіко-математичну модель.
Розв’язування. Нехай маємо n пунктів, де має побувати комівояжер.
Позначимо:
![]()
Отже, хij — бульові (цілочислові) змінні. Цільовою функцією цієї задачі є мінімізація всього маршруту комівояжера:
![]()
де сij — відстань між містами і та j.
Обмеження щодо одноразового в’їзду в кожне місто:
![]()
![]() .
.
Обмеження щодо одноразового виїзду з кожного міста:
![]()
![]() .
.
Ці
обмеження не повністю описують допустимі
маршрути і не виключають можливості
розриву маршруту. Щоб усунути цей
недолік, введемо додаткові змінні ui(uj)
![]() ,
які набувають невід’ємних цілих значень.
Запишемо обмеження, які виключають
можливість існування підмаршрутів:
,
які набувають невід’ємних цілих значень.
Запишемо обмеження, які виключають
можливість існування підмаршрутів:
![]()
![]() ,
,
де ui (uj) — порядковий номер міста за маршрутом прямування комівояжера.
Запишемо числову економіко-математичну модель комівояжера за розглядуваних умов.
Критерій оптимальності:
![]()
![]() ;
;
а) обмеження щодо одноразового в’їзду в кожне місто:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
б) обмеження щодо одноразового виїзду з кожного міста:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
в) обмеження щодо виключення підмаршрутів:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
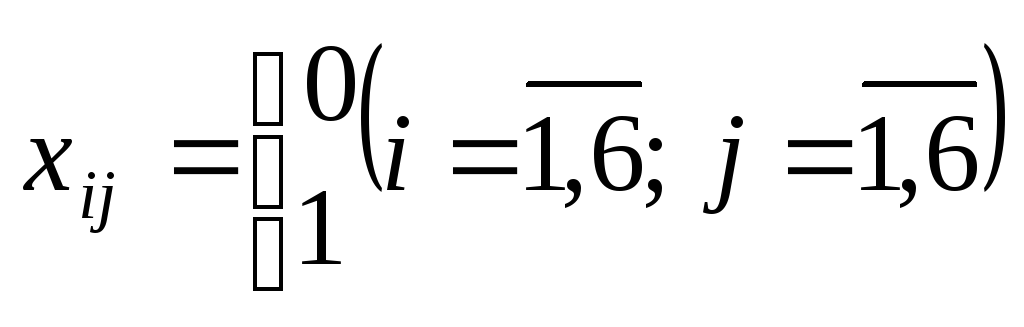 ,
,
ui(uj)
— цілі числа
![]() .
.
Такі задачі розв’язуються спеціальними методами [1; 10].
Зауважимо, що аналогічні задачі нерідко постають на практиці, наприклад, у дрібному бізнесі.
Фірма у місті має 25 кіосків, які торгують безалкогольними напоями. Щоденно з бази автомобілем розвозять до них товар. Як оптимально організувати розвезення відповідної кількості товару?
Задача 6.4.
|
Показник |
Вид продукції | ||
|
Озима пшениця, т |
Цукровий буряк, т |
Молоко, т | |
|
Постійні витрати, тис. грн. |
40 |
70 |
20 |
|
Поточні витрати на одиницю продукції, грн. |
400 |
150 |
500 |
|
Норма витрат ріллі, га |
0,2 |
0,02 |
0,25 |
|
Ціна одиниці продукції, грн. |
800 |
300 |
1000 |
Визначити оптимальний план виробництва продукції кожного виду, якщо з цією метою використовується 100 га ріллі.
Розв’язування.
Нехай xj
— обсяг виробництва j-го
виду продукції,
![]() .
Функція сумарних витрат на виробництвоj-ї
продукції набуває вигляду:
.
Функція сумарних витрат на виробництвоj-ї
продукції набуває вигляду:

Як цільову функцію беремо максимізацію валового прибутку:
![]()
де yj — ціна одиниці j-ї продукції.
Обмеження щодо ріллі:
![]()
де аj — норма витрат ріллі на одиницю j-ї продукції; А — ресурс ріллі.
Цільова функція цієї задачі не є лінійною, оскільки має розрив у початку координат. Отже, ця задача не може бути розв’язана симплексним методом.
Щоб розв’язати цю задачу, скористаємося штучним прийомом. Введемо бульові змінні такою умовою:
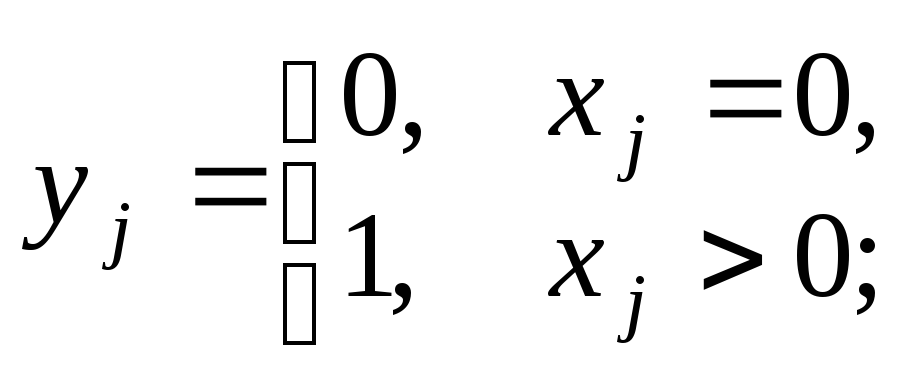
її можна записати у вигляді лінійної нерівності
![]()
![]() ,
,
де М
— досить велике число, за якого умова
![]()
![]() виконується для всіх допустимих обсягів
виробництва продукції.
виконується для всіх допустимих обсягів
виробництва продукції.
У результаті маємо таку економіко-математичну модель:
![]()
за умов
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Запишемо
числову економіко-математичну модель.
Очевидно, що максимум пшениці становить
![]() 500 т,
цукрових буряків —
500 т,
цукрових буряків —![]() 5000 т,
молока —
5000 т,
молока —![]() 400 т.
Отже,М може
дорівнювати 5000. Звідси маємо:
400 т.
Отже,М може
дорівнювати 5000. Звідси маємо:
![]()
за умов
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
Пропонуємо розв’язати аналогічну задачу, оцінивши ефективність нового бізнесу.
Звичайно, у реальній ситуації існує більший набір можливих видів продукції, а також багато обмежень щодо ресурсів.
Задача 6.5.
Оптимізувати режим функціонування виробничої лінії, яка охоплює 11 операцій з виготовлення двох виробів. Лінію обладнано одним багатоопераційним верстатом. Послідовність і тривалість (у хвилинах) виконання операцій відбиває рис. 6.3.
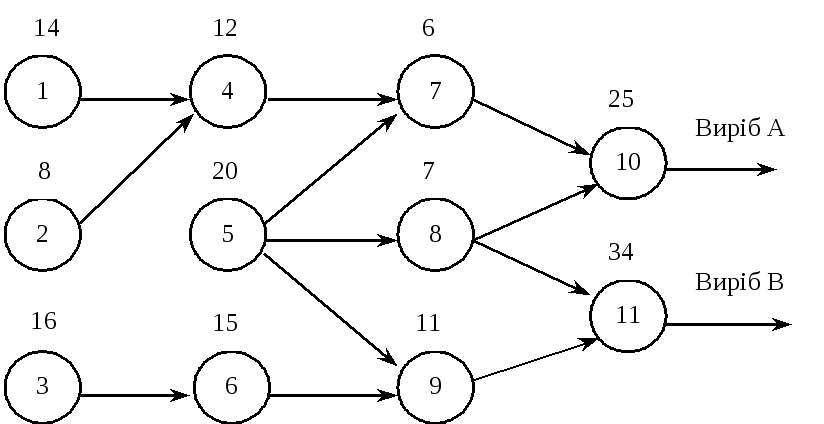
Рис. 6.3
Установлено термін виготовлення кожного з виробів А та В як проміжок часу від деякого початкового моменту. Нехай це буде відповідно 120 і 150 хв. Передбачається, що в кожний момент часу на верстаті може виконуватися одна операція.
Визначити оптимальний термін початку кожної операції.
Розв’язування. Розглянемо спочатку задачу в загальному вигляді, скориставшись позначеннями:
aj(k)
— час виконання j-ї
операції
![]() ;dj
— момент часу (термін) для j-го
виробу, до якого необхідно завершити
операцію j;
хj
— час (термін) початку j-ї
операції; t
— сумарний час виконання всіх операцій.
Економіко-математична модель містить
три типи обмежень.
;dj
— момент часу (термін) для j-го
виробу, до якого необхідно завершити
операцію j;
хj
— час (термін) початку j-ї
операції; t
— сумарний час виконання всіх операцій.
Економіко-математична модель містить
три типи обмежень.
1. Послідовність
виконання i-ї
операції записується для всіх пар
операцій
![]()
![]() якщоi-та
операція передує в часі j-й
операції.
якщоi-та
операція передує в часі j-й
операції.
2. Обмеження нерозгалуженості виробничого процесу для операцій і та j, які не виконуються одночасно (i ≠ j), має вигляд:
або xi – хj ≥ aj, якщо операція j передує в часі операції і; або xj – хi ≥ ai, якщо операція і передує в часі операції j.
Зауважимо, що логічні обмеження виду «або-або» не можуть входити до економіко-математичної моделі задачі лінійного програмування, оскільки породжують неопуклу множину допустимих розв’язків. Тому необхідно ввести допоміжні змінні, які дозволяють записати наведені щойно логічні умови у вигляді лінійних обмежень. Це такі бульові змінні:
![]()
Увівши змінні yij, запишемо шукані обмеження:
![]()
![]() ,
,
![]()
![]() ,
,
де М — досить велике число.
3. Обмеження щодо термінів виготовлення кожного виробу:
![]()
![]() ,
,
де j — остання операція для k-го виробу.
4. Усі операції мають бути виконанні до моменту часу t:
![]()
![]() .
.
Критерій оптимальності:
![]()
тобто ставиться задача, щоб обидва вироби були виготовлені за мінімальний час.
Запишемо числову економіко-математичну модель:
![]()
за наведених далі умов.
1. Послідовність виконання операцій:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Обмеження щодо нерозгалуженості виробничого процесу:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3. Обмеження щодо термінів виготовлення виробів:
![]() ,
,
![]() .
.
4. Усі операції мають бути виконані до моменту часу t:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
5. Обмеження на змінні:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Отже, маємо частково цілочислову задачу з бульовими змінними.
Задача 6.6.
Розподілити чотирьох робітників за чотирма видами устаткування так, щоб їх загальна продуктивність праці була максимальною. Дані стосовно продуктивності праці кожного робітника на устаткуванні кожного виду наведено в таблиці:
|
Робітник |
Продуктивність праці, грн./год, на устаткуванні | |||
|
1 |
2 |
3 |
4 | |
|
1 |
12 |
9 |
8 |
7 |
|
2 |
10 |
7 |
6 |
5 |
|
3 |
9 |
6 |
4 |
4 |
|
4 |
8 |
5 |
3 |
2 |
Розв’язування. Дану задачу можна розглядати як транспортну, в якій робітники ототожнюються з постачальниками вантажів, а види устаткування — зі споживачами цих вантажів. Обсяги пропозиції та попиту в кожному випадку дорівнюють одиниці. Отже, змінні будуть бульовими:
![]()
Якщо cij — продуктивність праці і-го робітника на j-му устаткуванні, то економіко-математичну модель про призначення у загальному вигляді можна записати так:
![]()
за умов
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
Числова модель набирає вигляду:
![]()
![]()
за умов
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() —цілі
числа
—цілі
числа
![]() .
.
З огляду на особливу структуру цієї задачі, зокрема її «транспортний» характер та рівність правих частин обмежень, для розв’язування можна застосувати ефективніший алгоритм, ніж для звичайної задачі цілочислового програмування з бульовими змінними. Пропонуємо читачеві ознайомитися з такими алгоритмами самостійно [9; 38].
