
Algebra_i_geometriya / ІІ модуль / NE_2.1 / Завдання для самостійної роботи до НЕ 2
.1.docЗавдання для самостійної роботи студентів:
-
За допомогою алгоритму Евкліда обчислити найбільший спільний дільник многочленів
 та
та
 .
.
-
Знайти найбільший спільний дільник многочленів
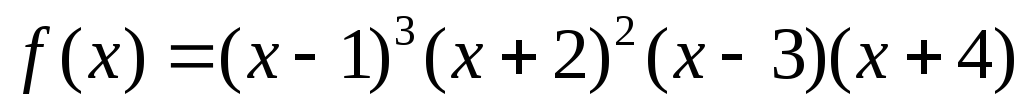 та
та
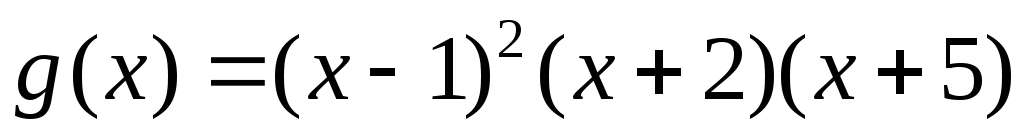 .
. -
Для многочленів
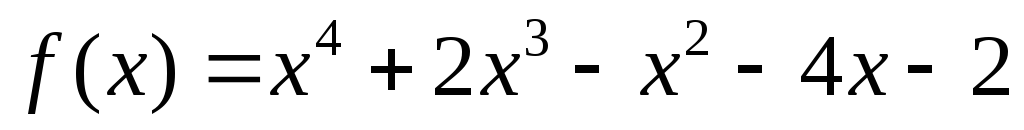 та
та
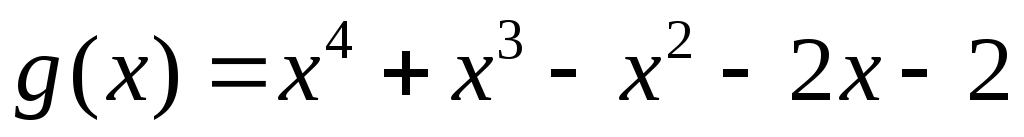 побудувати многочлени
побудувати многочлени
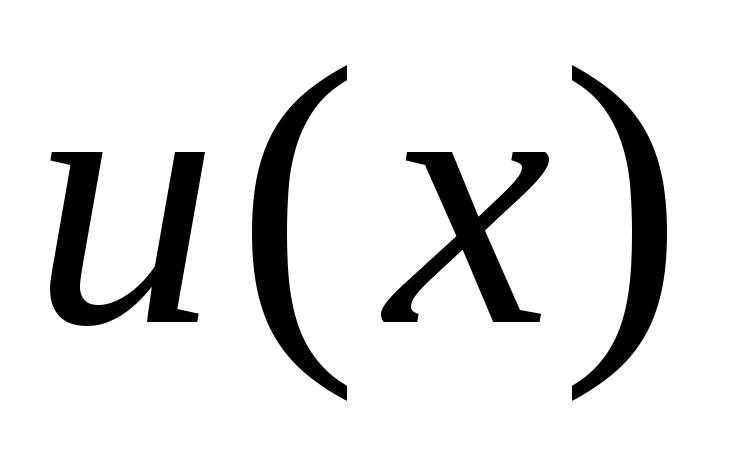 та
та
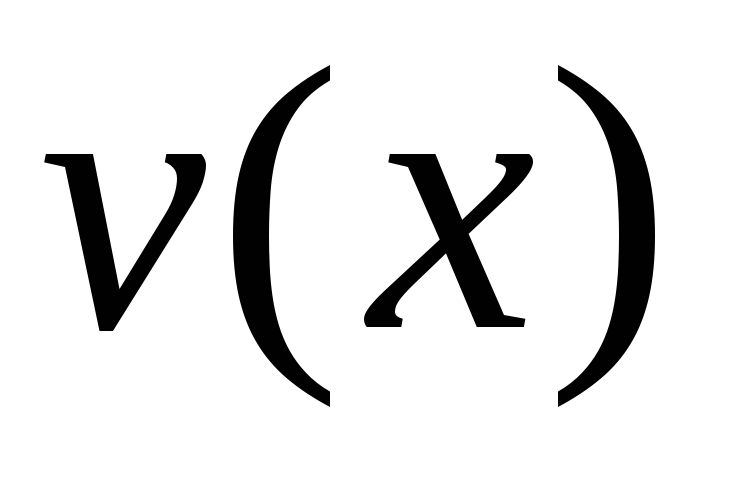 ,
які задовольняють рівність
,
які задовольняють рівність
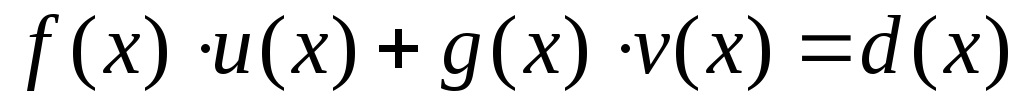 ,
де
,
де
 ,
використовуючи: а) алгоритм
Евкліда; б) метод невизначених
коефіцієнтів.
,
використовуючи: а) алгоритм
Евкліда; б) метод невизначених
коефіцієнтів. -
Розділити многочлен
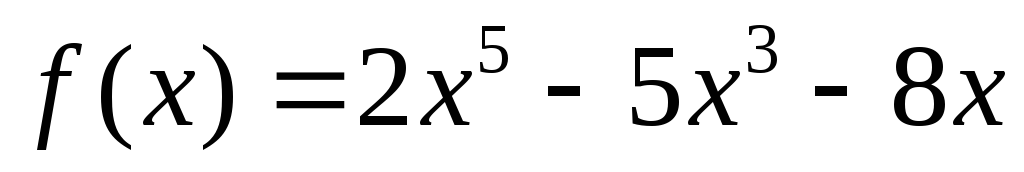 з остачею на
з остачею на
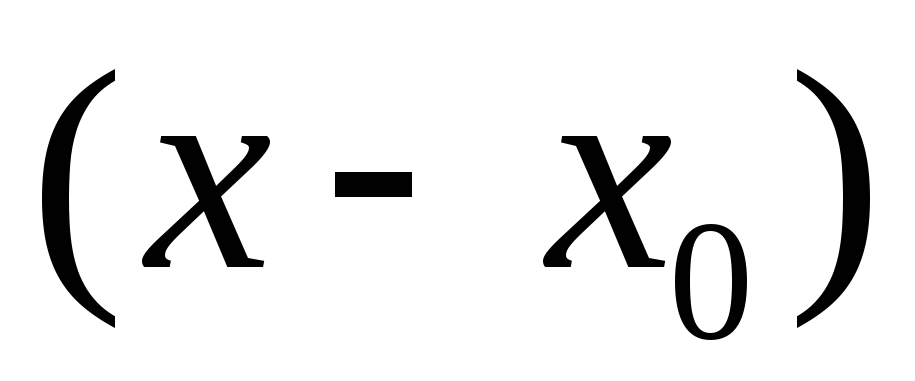 та обчислити значення
та обчислити значення
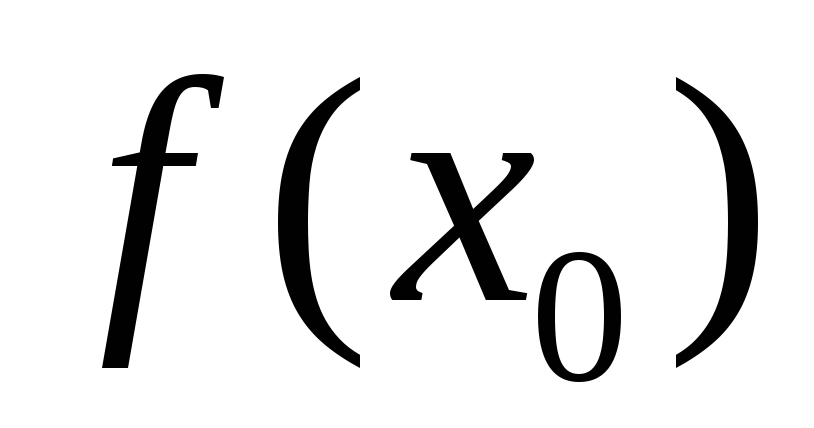 ,
якщо: а)
,
якщо: а)
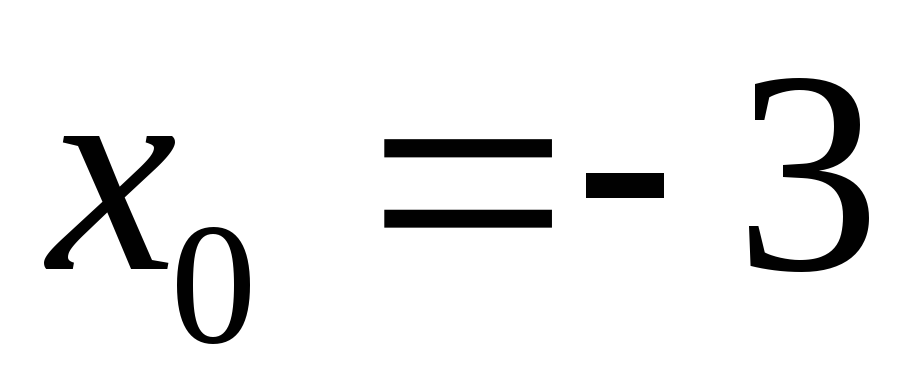 ;
б)
;
б)
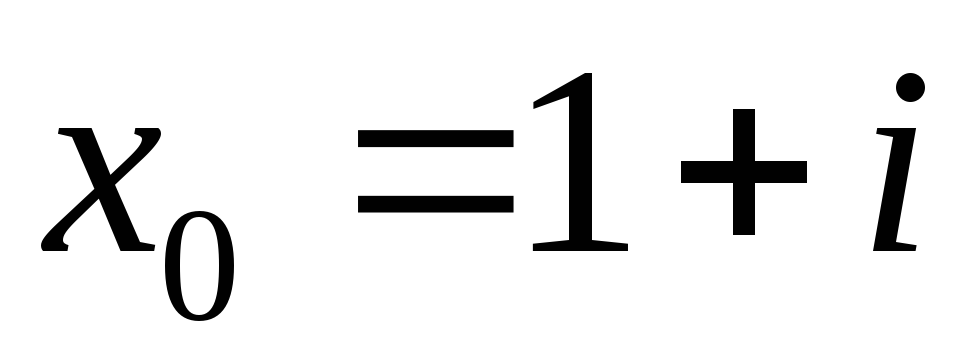 .
. -
Знайти значення многочлена
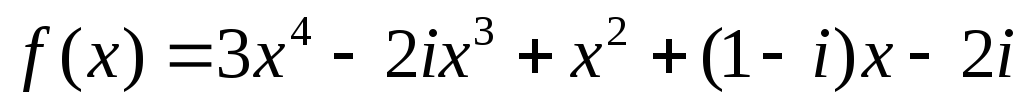 при: а)
при: а)
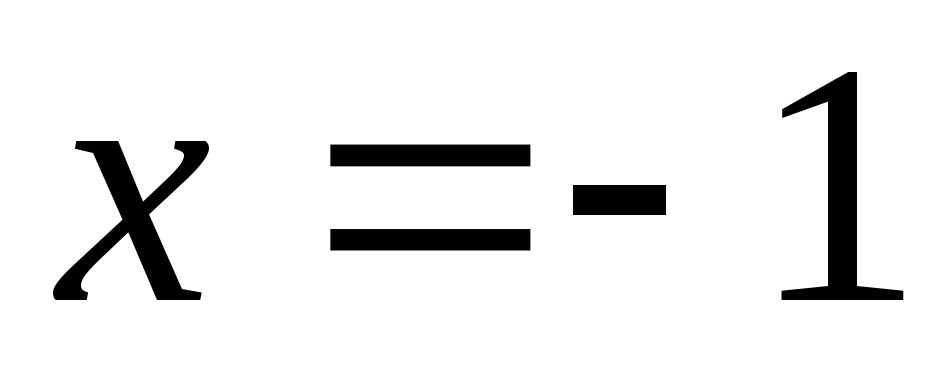 ;
б)
;
б)
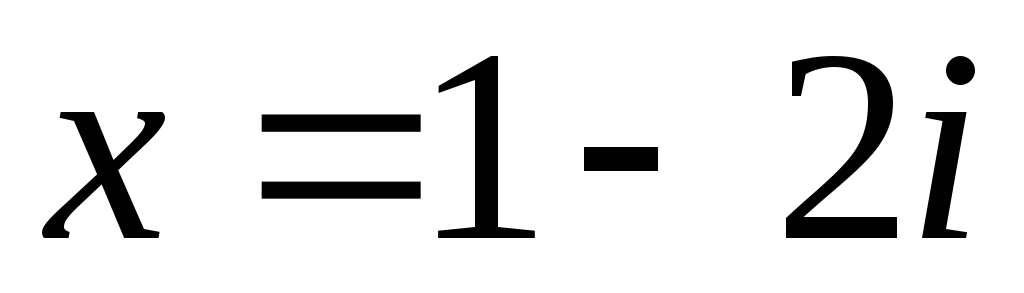 .
. -
Користуючись схемою Горнера, розкласти за степенями
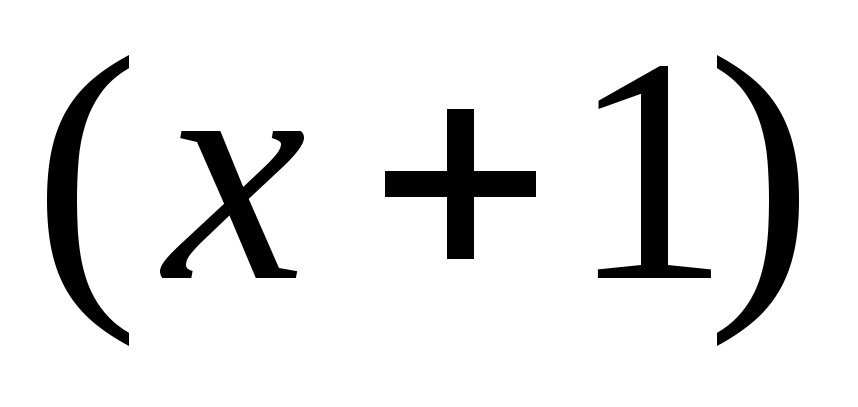 многочлен
многочлен
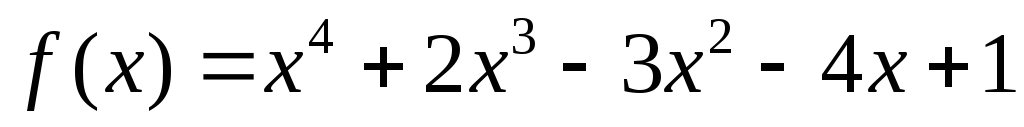 .
.
-
Виписати значення многочлена
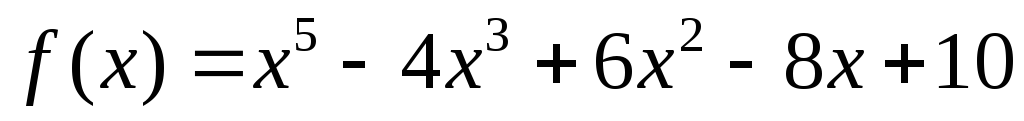 та всіх його похідних при
та всіх його похідних при
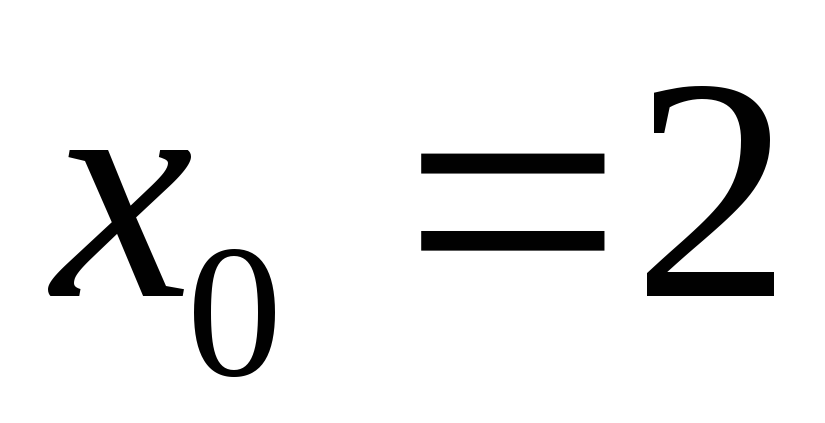 .
. -
Знайти значення для коефіцієнта
 так, щоб многочлен
так, щоб многочлен
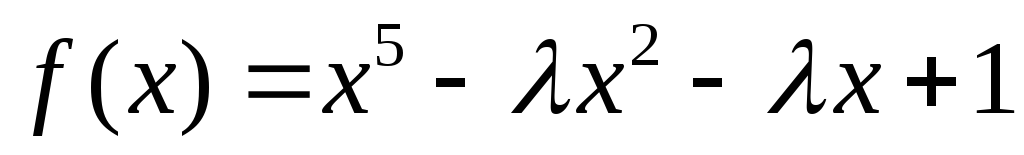 мав число
мав число
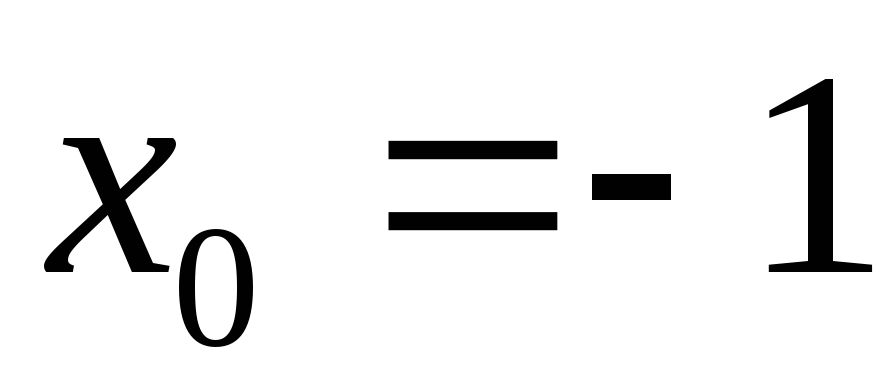 коренем не нижче другої кратності.
коренем не нижче другої кратності. -
При яких значеннях
 та
та
 многочлен
многочлен
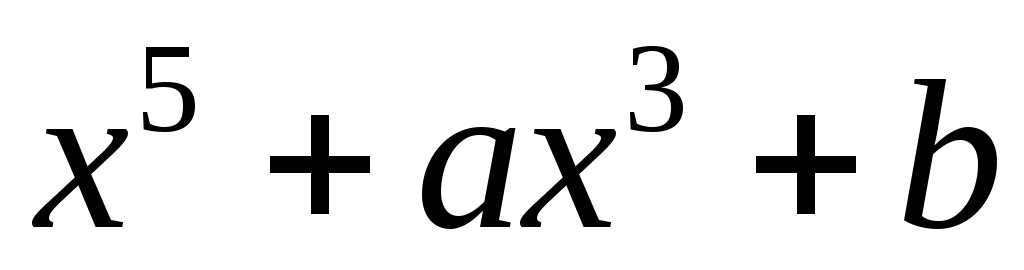 має двократний ненульовий
корінь?
має двократний ненульовий
корінь? -
Довести, що многочлен
 має число
має число
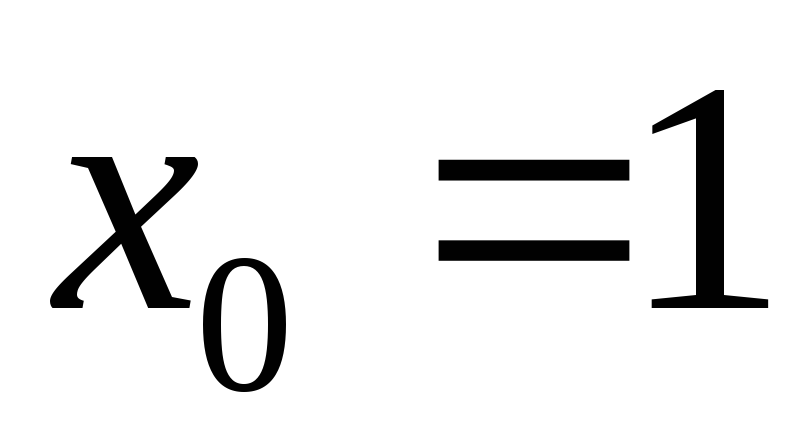 трикратним коренем.
трикратним коренем.
-
Чому дорівнює кратність кореня
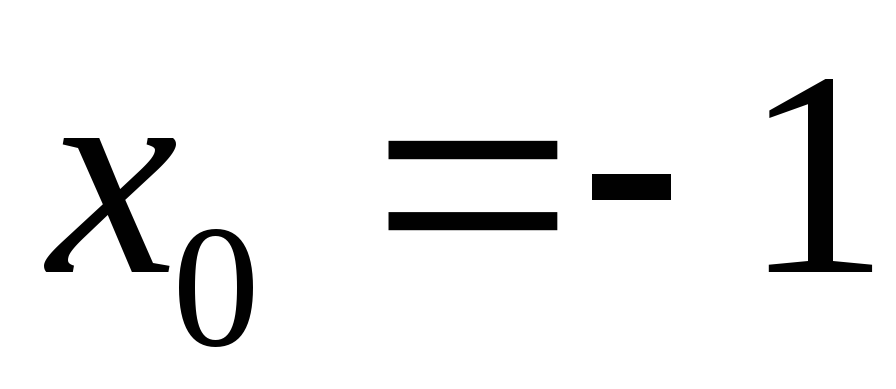 для многочлена
для многочлена
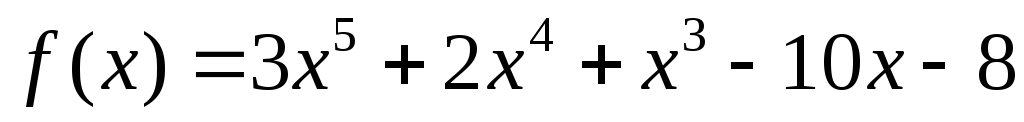 ?
? -
Розкласти на суму простіших дробів І і ІІ типу дріб: а)
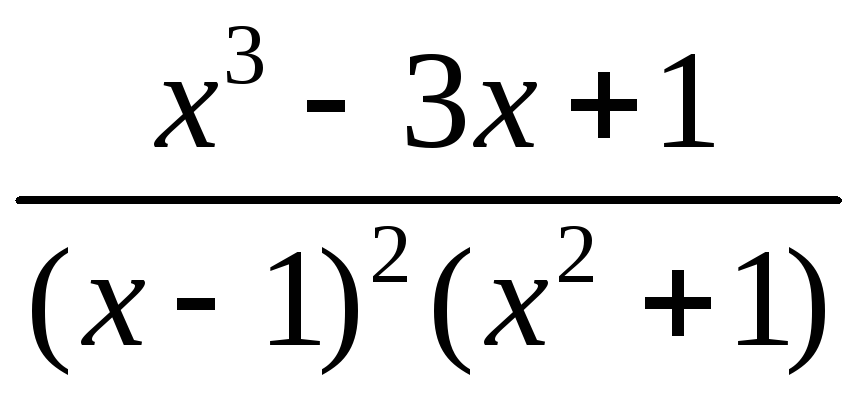 ;б)
;б)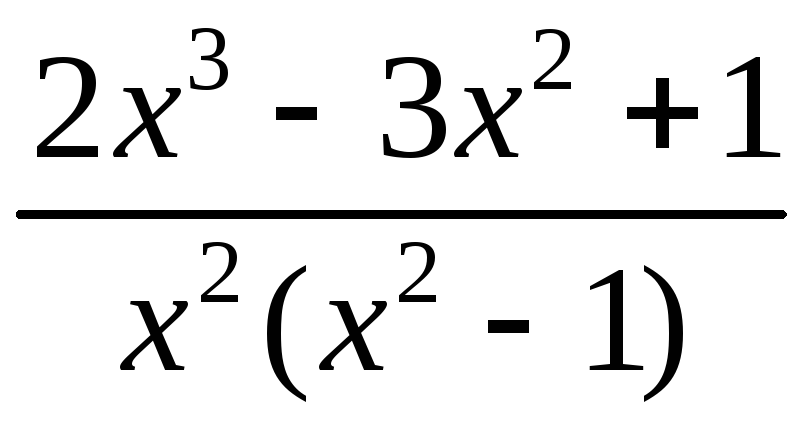 ;в)
;в)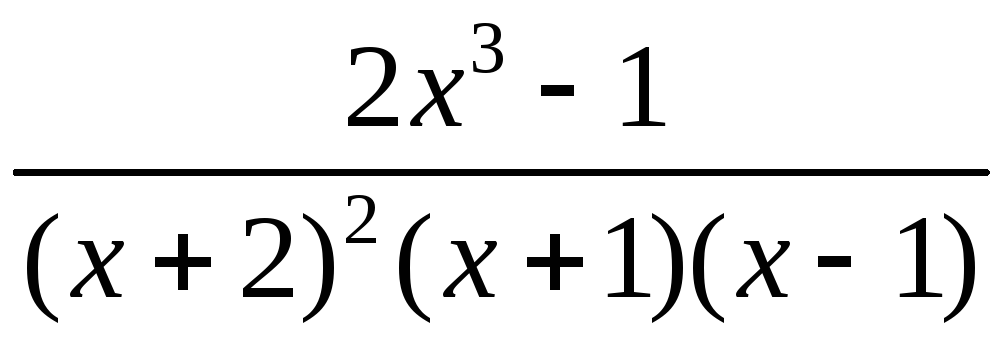 .
. -
Побудувати многочлен четвертого степеня зі старшим коефіцієнтом 1, який має: а) корені
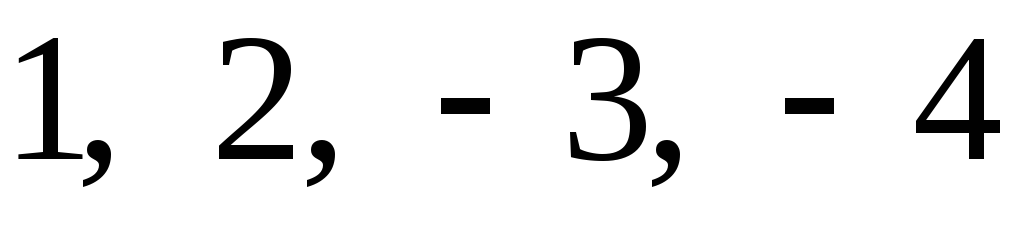 ;
;
б)
трикратний корінь –1 та простий корінь
![]() ;
;
в)
дійсні коефіцієнти та корені
![]() та
та
![]() .
.
-
Знайти многочлен найменшого степеня за таблицею його значень:
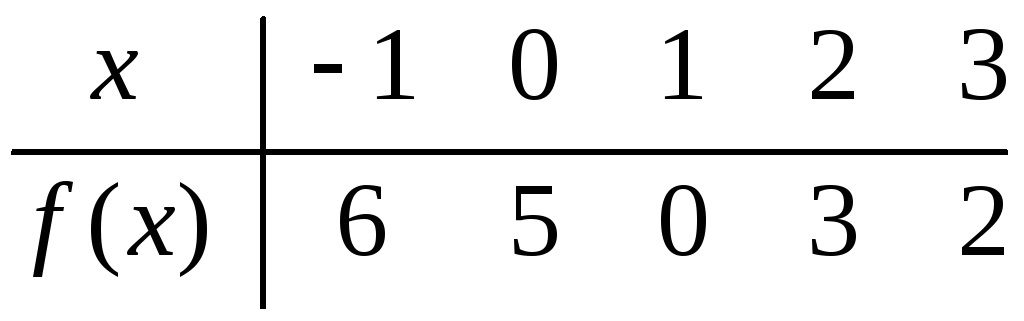 .
. -
Знайти раціональні корені многочлена:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
-
Використовуючи теорему Штурма, відокремити дійсні корені многочлена:
а)
![]() ;
;
б)
![]() .
.
