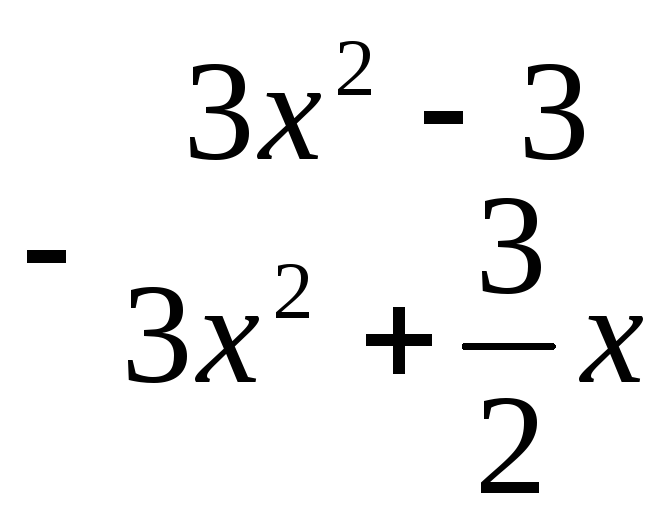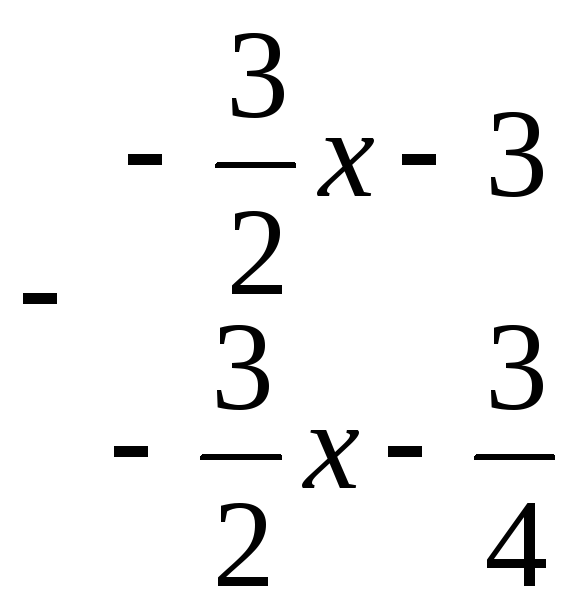Algebra_i_geometriya / ІІ модуль / NE_2.1 / Практичні заняття до НЕ 2

Приклад 11. Побудувати многочлен четвертого степеня зі старшим коефіцієнтом 1, який має:

а) корені 1, 7, -3, -4;

б) трикратний корінь –1 та простий корінь і;

в) дійсні коефіцієнти та корені 2-і та 1+2і.

Розв.

а) ‑ шуканий многочлен, у якого ‑ корені.

Тоді

‑ згідно з наслідком з основної т-ми алгебри. Отже:

‑ шуканий многочлен.

б) ‑ шуканий многочлен.

в)

Оскільки шуканий многочлен має дійсні коефіцієнти, то він має ще два корені, спряжені до та :

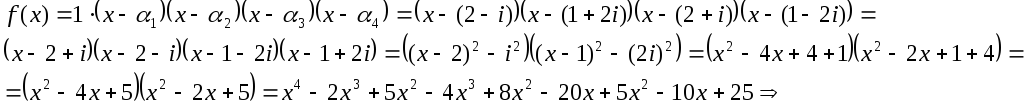
Отже, ‑ шуканий многочлен.

Приклад12. Знайти многочлен найменшого степеня за таблицею його значень:

	-1	0	1	2	3
	6	5	0	3	2

Розв. Скористаємося формулою Лагранжа:

де

Отже маємо:

Тому

Отже, ‑ шуканий многочлен.

Приклад 13. Знайти раціональні корені многочлена:

а)

Розв. Шукаємо спочатку цілі корені цього многочлена. Вони, якщо є, то є дільниками вільного члена . Тобто

Зменшимо степінь многочлена поділивши його на

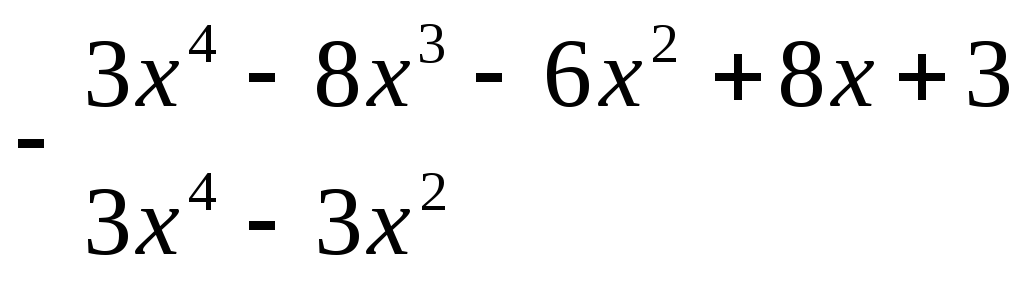
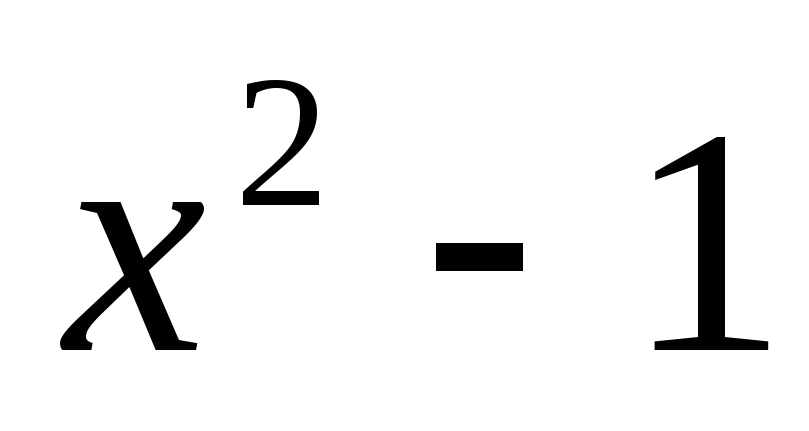
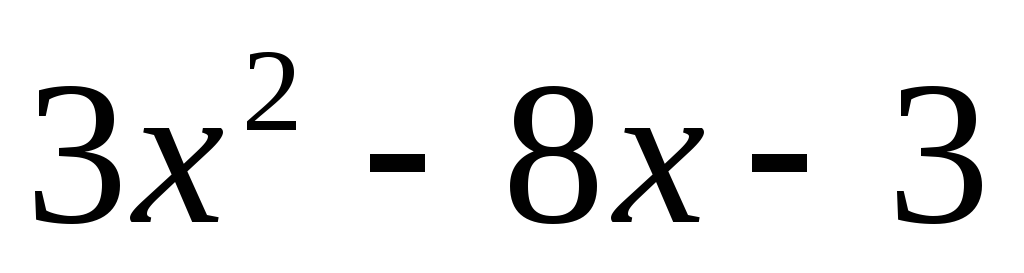
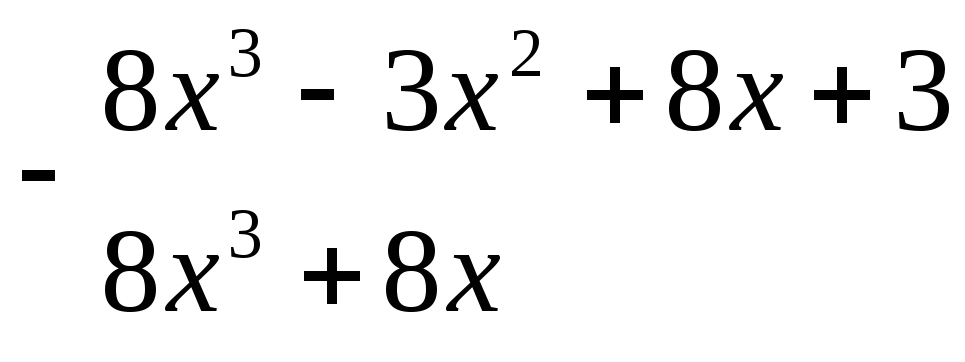
	0

Отже,

Знайдемо тепер корені многочлена

Отже,

В-дь: Раціональні корені многочлена

б)

Цілі корені даного многочлена, якщо існують, є дільниками вільного члена

	2	-1	-14	19	-6
1	2	1	-13	6	0

Отже,

‑ шукаємо його корені

та ‑ одночасно цілі

та

Можливі корені: 2; -3; ‑ Перев. за схемою Горнера.

	2	1	-13	6
2	2	5	-3	0
-3	2	-1	0

‑ корінь

‑ корінь

Отже,

Звідси має 4 корені:

в)

‑ дільники вільного члена

‑ корінь

та ‑ одночасно цілі

та ‑ одночасно цілі

Можливі корені: 2; -2; 3; -3; ‑ Перевіряємо за схемою Горнера.

	3	17	27	7	-6
2	3	23	73	153	3000
-2	3	11	5	-3	0
3	3	26	105	322	9600
-3	3	8	3	-2	0

Дробові корені мн-на знах. серед всіх нескоротних дробів вигляду , де ‑ дільники

‑ дільники (), .

‑ можливі корені.

та ‑ одночасно цілі.

та

Можливі корені:

Скористаємося схемою Горнера:

	3	17	27	7	-6
	3
	3
	3	18	33	18	0

‑ корінь .

Оскільки ‑ многочлен 4-го степеня, то в нього не більше 4-х дійсних коренів. Отже,

‑ шукані корені .

Приклад 14. Використовуючи теорему Штурма, відокремити дійсні корені многочлена:

а)

Розв.

Отже, система многочленів Штурма для даного така:

Будуємо таблицю для знаходження к-ті знакозмін у системі Штурма:

	-	+	-	+	3
0	+	-	-	+	2
	+	+	+	+	0

а) на інтерв. має 1 корінь;

б) на інтерв. має 2 корені.

Оскільки ‑ многочлен 3-го степеня, із якого 1 від’ємний та 2 додатні корені, то це означає, що всі його корені дійсні. Відокремимо тепер кожен з них.

1	-	+	+	+	1
2	+	+	+	+	0
-1	+	‑	‑	+	2
-2	+	‑	‑	+	2
-3	+	+	‑	+	2
-4	+	+	‑	+	2
-5	‑	+	‑	+	3

на (0;1) – 1 корінь

Отже, многочлен має три дійсні корені

б)

Розв.

Отже, система множників Штурма має вигляд:

	‑	+	‑	+	3
0	‑	‑	+	+	1
	+	+	+	+	0
1	‑	0	+	+	1
2	+	+	+	+	0
-1	+	0	‑	+	2
-2	‑	+	‑	+	3

На інтервалі є корені;

На інтервалі є корінь.

Отже, має 3 дійсні корені:

15