Algebra_i_geometriya / ІІІ модуль / NE_3.1 / Завд. для сам. роб

Завдання для самостійної роботи студентів:

1. Довести, що множина всіх многочленів степеня не вище 3 з дійсними коефіцієнтами, для яких , утворює дійсний лінійний простір. Вказати приклад бази та розмірність цього простору.

2. Довести, що сукупність усіх векторів-рядків довжини 5, у яких друга координата у три рази більша за останню, утворює дійсний лінійний простір. Знайти деякий базис і координати вектора 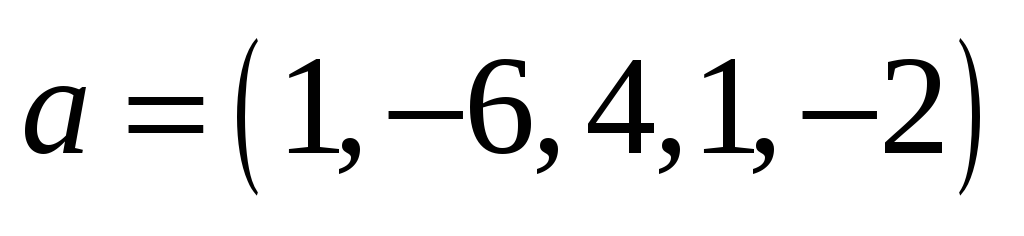у вибраному базисі.

3. Довести, що сукупність всіх симетричних матриць 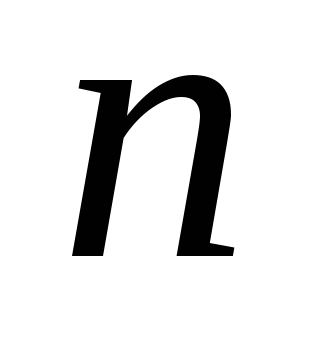-го порядку з дійсними елементами утворює дійсний лінійний простір. Знайти його розмірність та виписати приклад бази.

4. Довести, що множина матриць третього (четвертого) порядку, симетричних відносно обох діагоналей, з дійсними елементами, утворює дійсний лінійний простір. Знайти довільний базис і розмірність цьо­го простору.

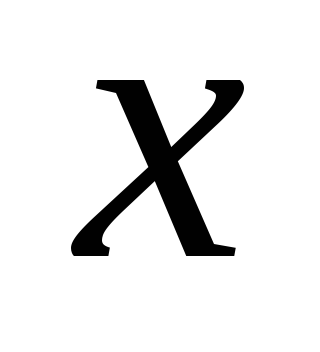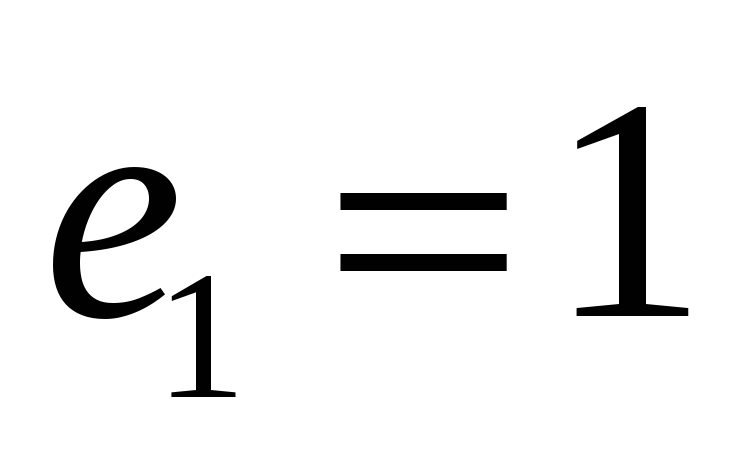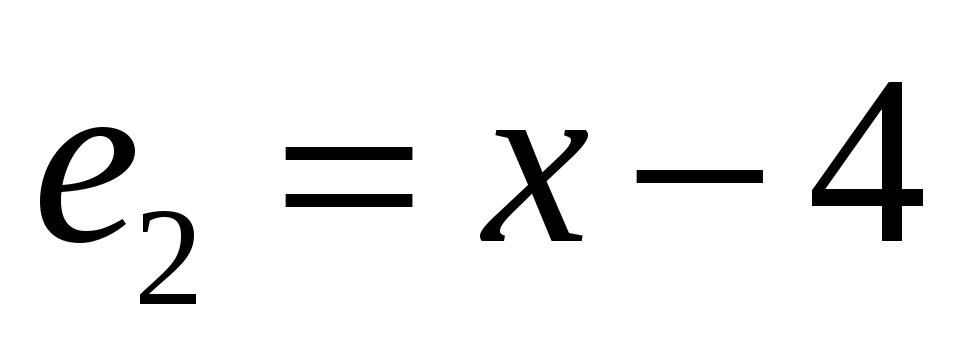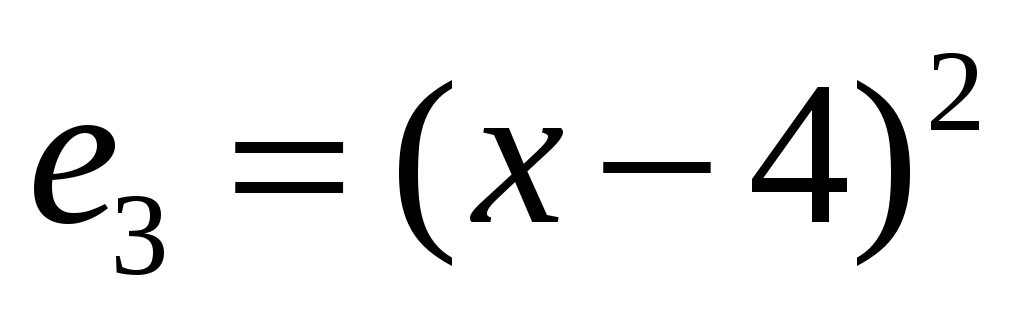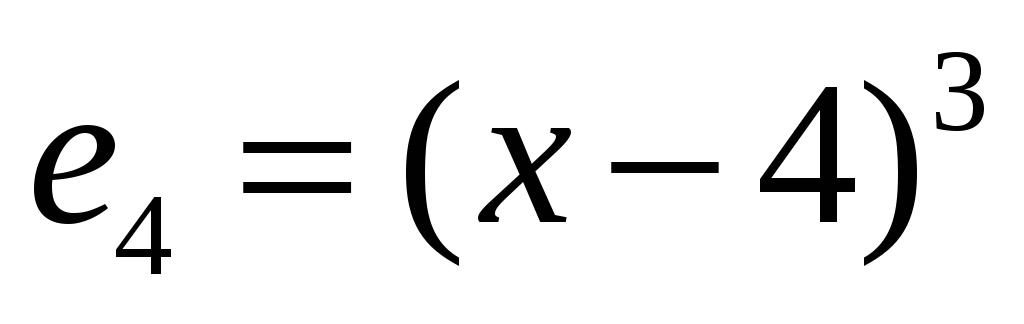5. У дійсному лінійному просторі многочленів від степеня не вище 3 знайти матрицю пе­реходу від базису , , , до базису , , , .

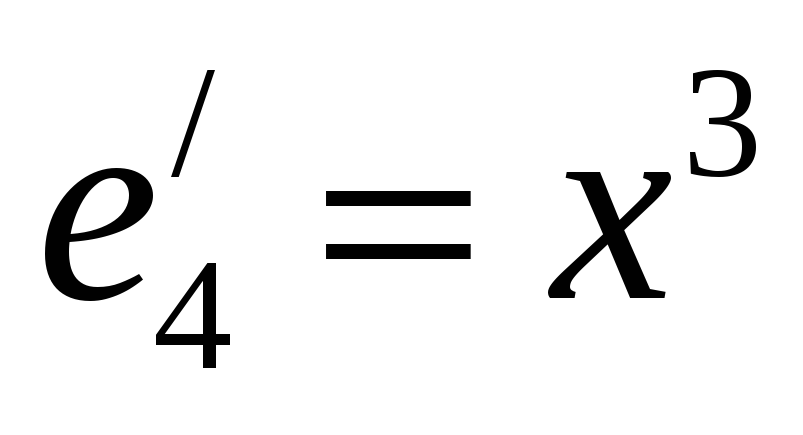6. У дійсному лінійному просторі знайти матрицю переходу від базису до базису: а) 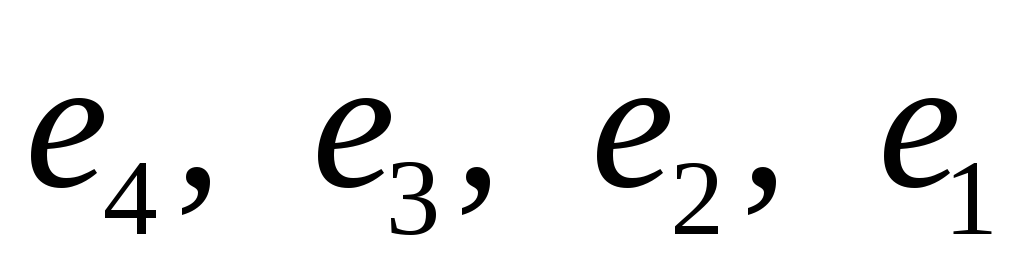; б) .

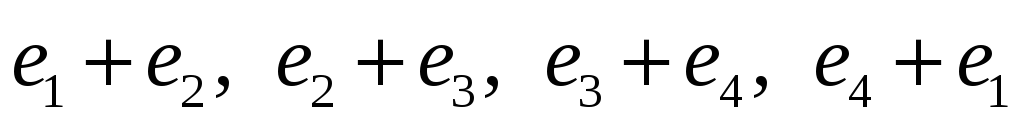7. Переконатися, що многочлени 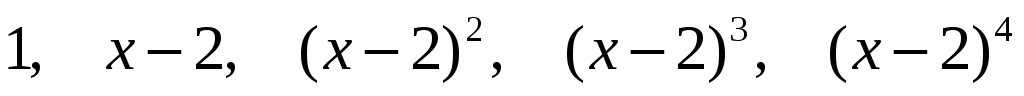утворюють базис у лінійному просторі многочленів степеня не вище 4. Знайти координати многочлена 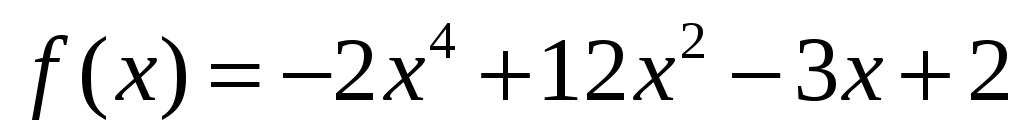у цьому базисі.

8. Довести, що кожна з систем векторів , 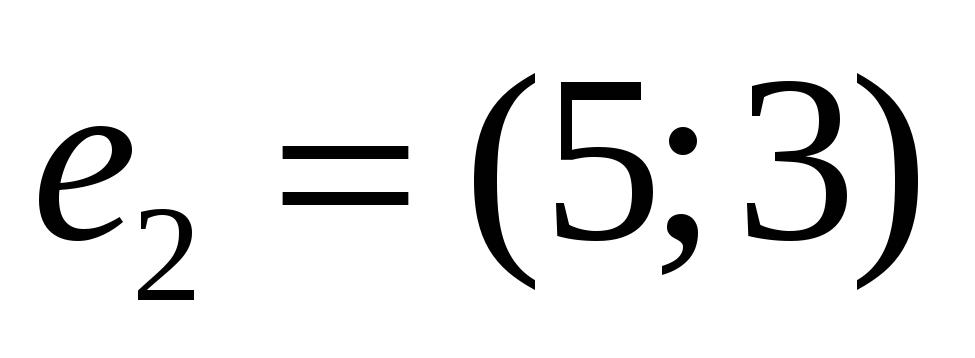та 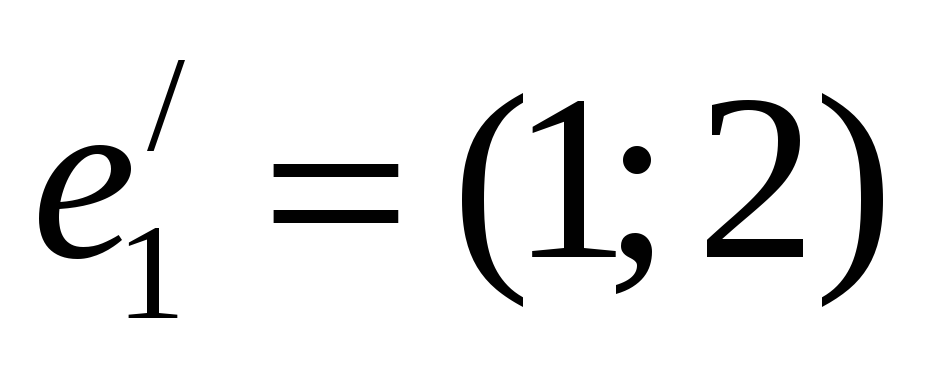, є базисом лінійного простору . Знайти зв’язок між координатами одного і того ж вектора відносно цих базисів.

9. Знайти розмiрнiсть суми i перетину лiнiйних пiдпросторiв, натягнутих на системи векторiв 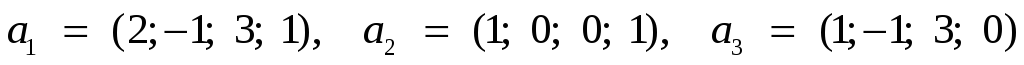та .

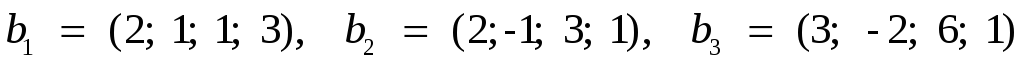10. Нехай –– оператор диференціювання у лінійному просторі многочленів степеня не вище 2 (тобто для довільного многочлена : 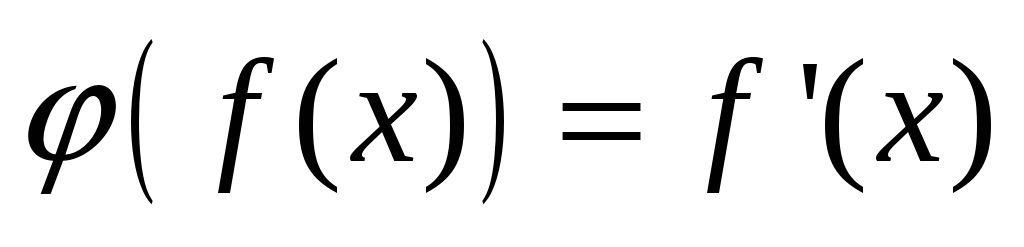). Знайти матрицю цього оператора у базисі , , .

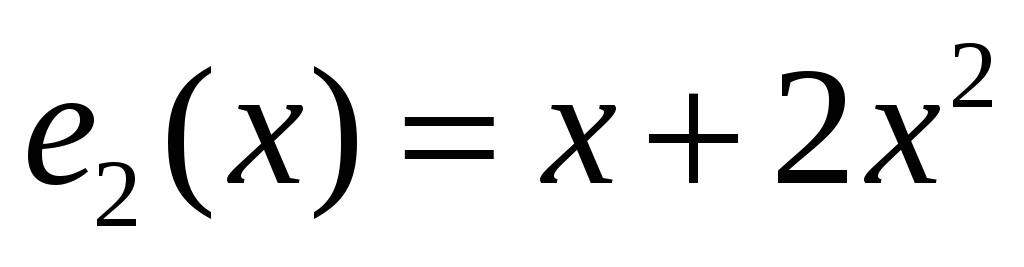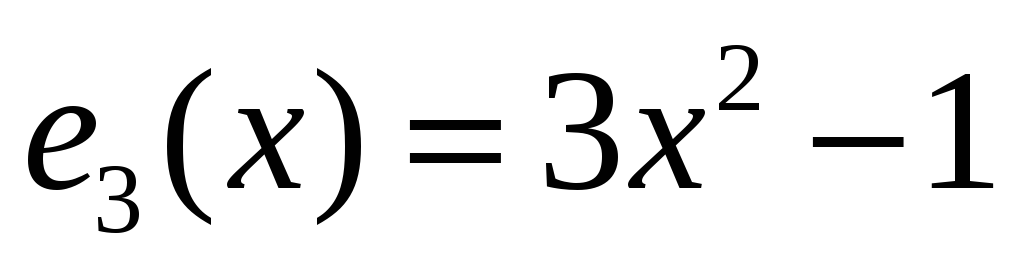11. У дiйсному лiнiйному просторi многочленiв f(x) степеня не вище 4 задано оператор 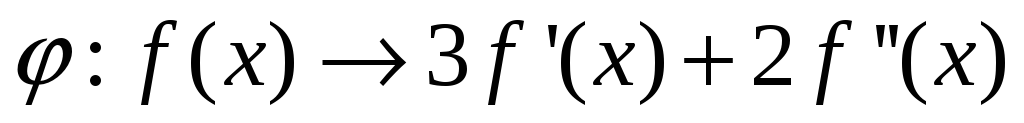. Довести, що цей оператор лiнiйний i знайти його матрицю в базi , , , , .

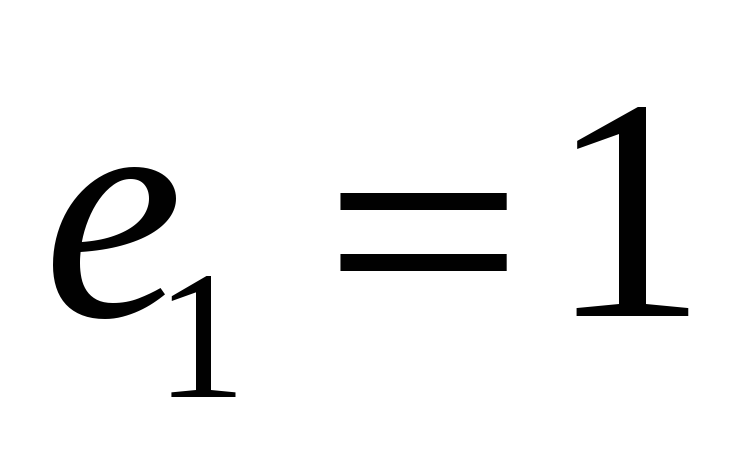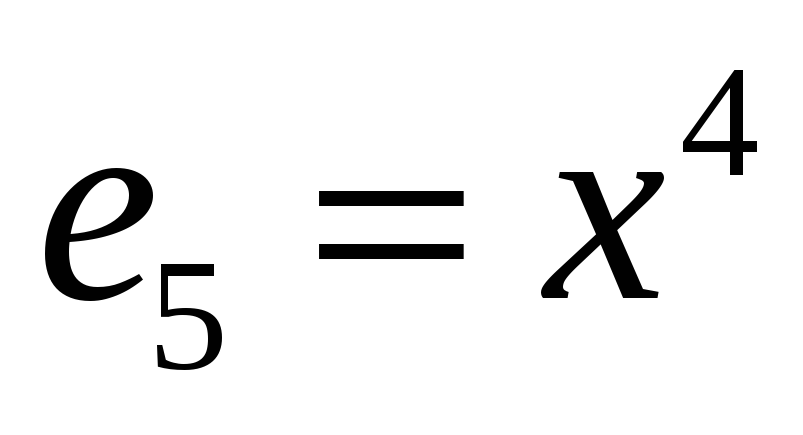12. Довести, що є лінійним оператор простору векторів з дійсними координатами (у якому визначене звичайне скалярне множення векторів), котрий діє за правилом 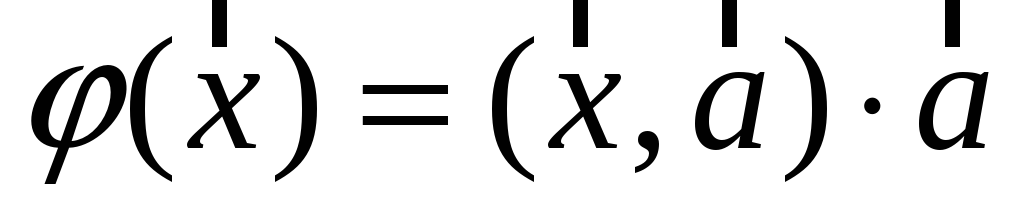, де . Знайти матрицю цього оператора в базисі , , .

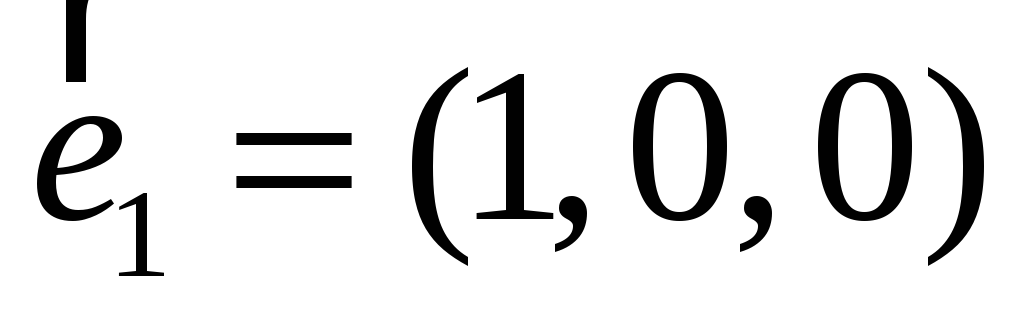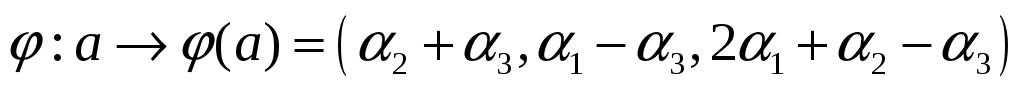13. Задано дiйсний лiнiйний простiр i оператор . Довести, що –– лiнiйний оператор i знайти його матрицю в базi .

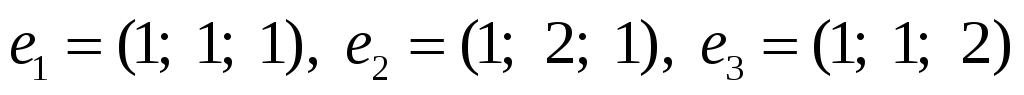14. Знайти матрицю оператора Х Х 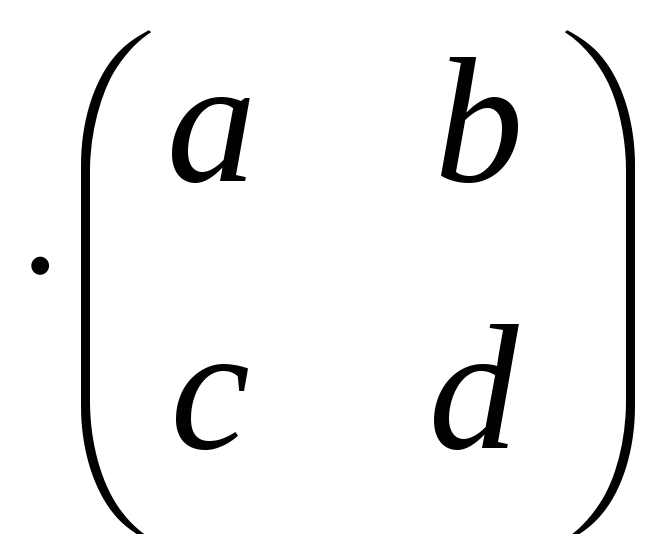() у просторі матриць другого порядку з дійсними елементами у базисі ,

, , .

15. Лінійний оператор у базі , , 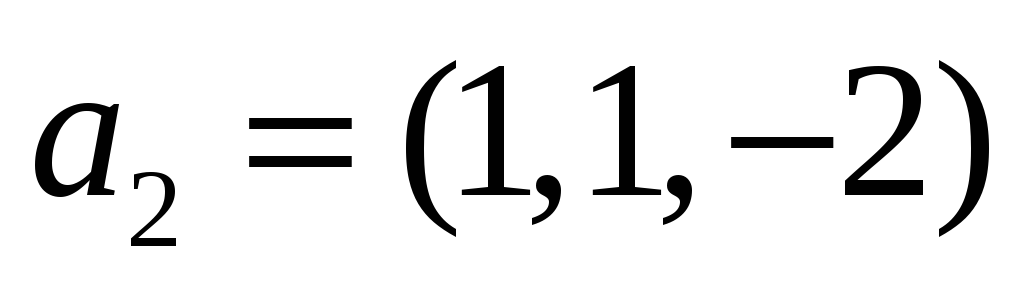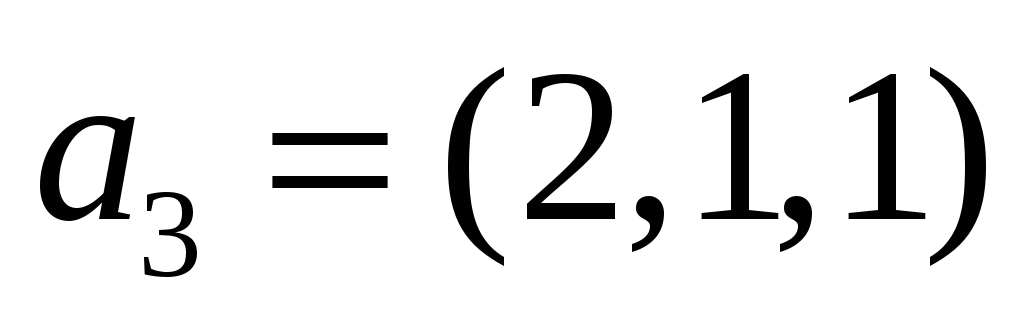задано матрицею . Знайти матрицю цього оператора в базисі , , .

16. Знайти ядро та образ лінійного оператора, заданого в деякому базисі матрицею . Чому дорівнює ранг та дефект цього оператора?

17. Знайти образ і ядро лінійного оператора:

а) , де ;

б) ; в) .

18. Знайти власні значення та власні вектори лінійноих операторів, що задаються в деякому базисі матрицею:

; ; .

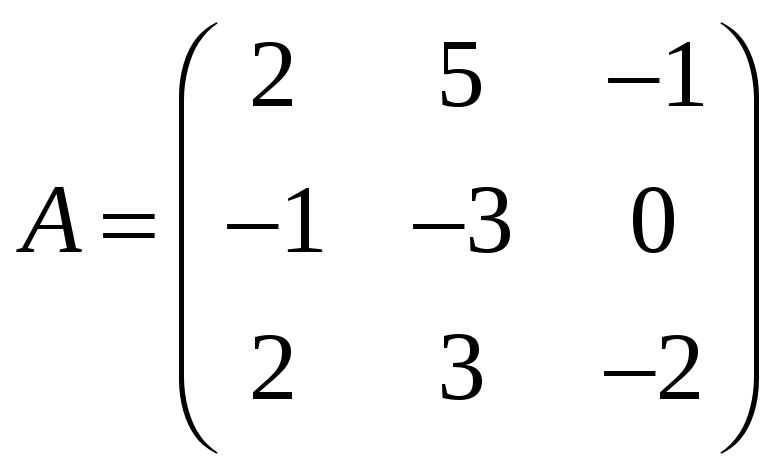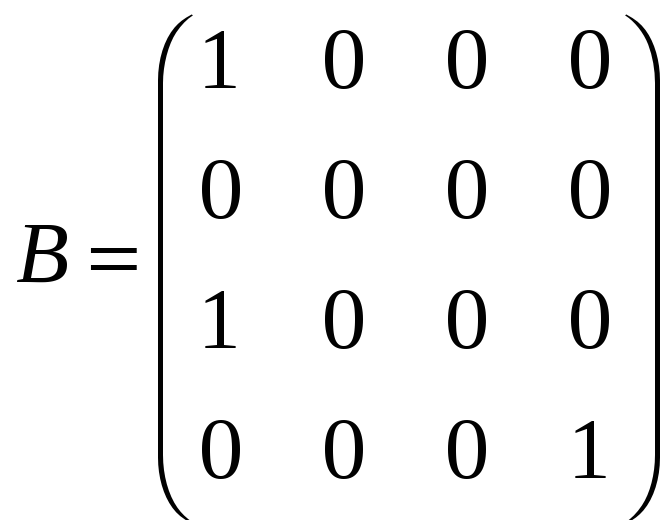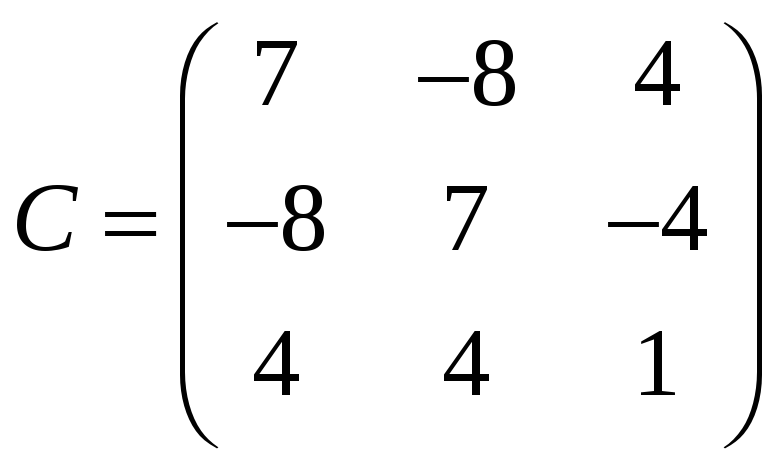19. З'ясувати, які з наступних матриць можна звести до діагонального виду шляхом переходу до нового базису ; .

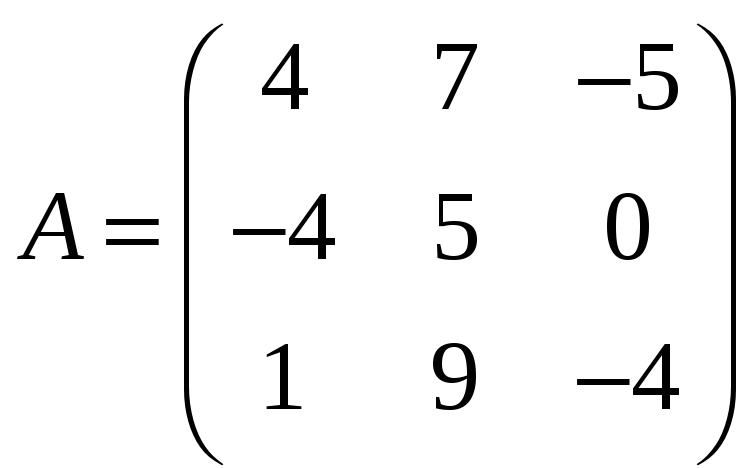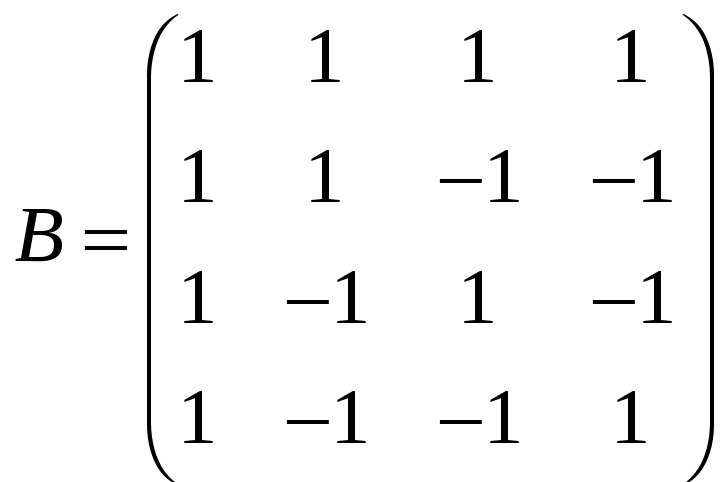2