5. Методи побудови математичних функцій

5.1. Загальний вигляд

Методи, розглянуті для правил і дерев рішень, працюють найбільш природно з категоріальними змінними. Їх можна адаптувати для роботи з числовими змінними, проте існують методи, які найбільш природно працюють з ними.

При побудові математичної функції класифікації або регресії основне завдання зводиться до вибору найкращої функції з усієї множини варіантів. Справа в тому, що може існувати безліч функцій, однаково класифікуючих одну і ту ж навчальну вибірку. Дана проблема проілюстрована на рис. 5.

Рис. 5. Варіанти лінійного поділу навчальної вибірки

Кожна з трьох ліній успішно поділяє всі точки на два класи (представлені на малюнку квадратами і кружками), проте модель повинна бути представлена однією функцією, яка найкращим чином вирішить завдання для нових об'єктів.

У результаті завдання побудови функції класифікації і регресії можна формально описати як завдання вибору функції з мінімальним ступенем помилки:

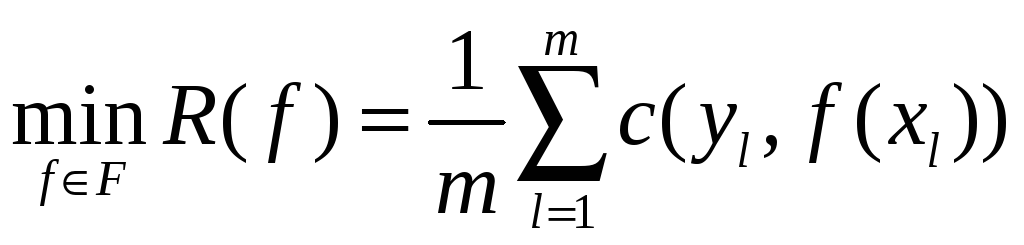, (5.1)

де – множина всіх можливих функцій; – функція втрат (loss function), в якій значення залежної змінної, знайдене за допомогою функції / для вектора , – її точне (відоме) значення.

Слід зазначити, що функція втрат враховує невід'ємні значення. Це означає, що неможливо отримати "винагороду" за дуже хороший прогноз. Якщо вибрана функція втрат все ж враховує від'ємні значення, то це легко виправити, вводячи позитивний зсув (можливо, із залежністю від ). Такими ж простими засобами можна домогтися нульових втрат при абсолютно точному прогнозі . Переваги подібного обмеження функції втрат полягають в тому, що завжди відомий мінімум і відомо, що він досяжний (принаймні, для даної пари ).

Для задач класифікації і регресії такі функції мають різний вигляд. Так, у випадку бінарної класифікації (приналежності об'єкта до одного з двох класів; далі перший клас позначається через +1, а другий клас через-1) найпростіша функція втрат (звана "0-1 loss" в англомовній літературі) приймає значення 1 у випадку неправильного прогнозу і 0 в іншому випадку:

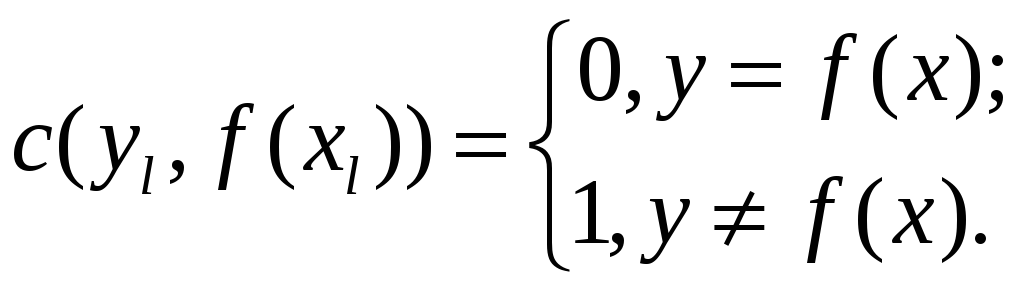
Тут не враховується ні тип помилки ( – позитивна помилка), ( – негативна помилка), ні її величина.

Невелика зміна дозволяє врахувати характер помилки:

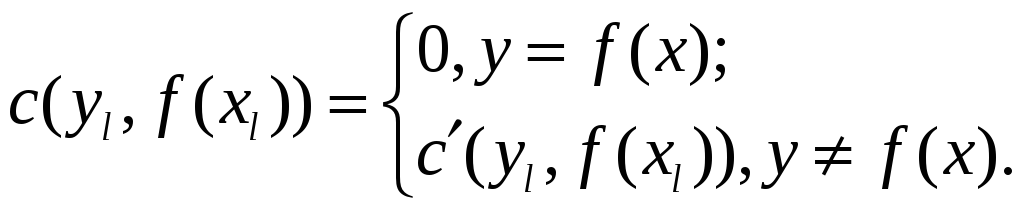
Тут може враховувати багато параметрів класифікованого об'єкта і характер помилки.

Ситуація ускладнюється у випадку класифікації з числом класів більше двох. Кожен тип помилки класифікації в загальному випадку вносить свій тип втрат таким чином, що виходить матриця розміру (де – число класів).

При оцінці величин, що приймають дійсні значення, доцільно використовувати різницю для оцінки якості класифікації. Ця різниця у разі регресії має цілком певний сенс (наприклад, розмір фінансових втрат при неправильній оцінці вартості фінансового інструменту на ринку цінних паперів). Враховуючи умову незалежності від положення, функція втрат буде мати вигляд

.

Найчастіше застосовується мінімізація квадратів різниць . Цей варіант відповідає наявності адитивного нормально розподіленого шума, що впливає на результати спостережень .

Відповідно, мінімізуємо:

. (5.2)

5.2. Лінійні методи. Метод найменших квадратів

Розрізняють два види функцій: лінійні і нелінійні. У першому випадку функції множини мають вигляд

,

де – коефіцієнти при незалежних змінних.

Завдання полягає в знаходженні таких коефіцієнтів , щоб задовольняти умову (5.1). Наприклад, при вирішенні завдання регресії, використовуючи квадратичну функцію втрат (5.2), і множину лінійних функцій :

,

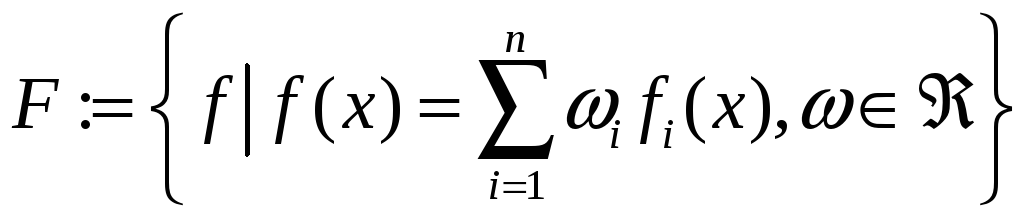де .

Необхідно знайти рішення наступного завдання:

.

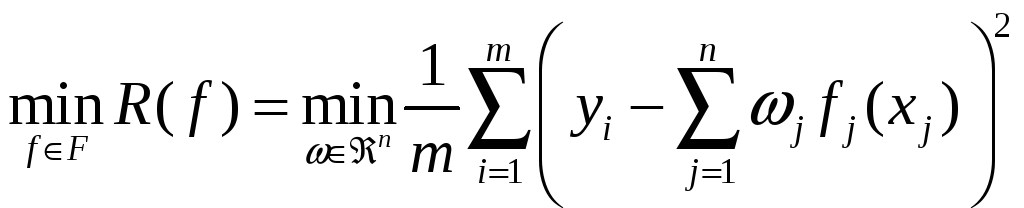Обчислюючи похідну по і вводячи позначення , отримуємо, що мінімум досягається за умови:

.

Рішенням цього виразу буде:

.

Звідки і виходять шукані коефіцієнти . Розглянутий приклад ілюструє пошук оптимальної функції методом найменших квадратів.

5.2. Нелінійні методи

Нелінійні моделі краще класифікують об'єкти, проте їх побудова більш складна. Завдання також зводиться до мінімізації виразу (5.1). При цьому множина містить нелінійні функції.

У найпростішому випадку побудова таких функцій все-таки зводиться до побудови лінійних моделей. Для цього початковий простір об'єктів перетвориться до нового:

.

У новому просторі будується лінійна функція, яка у вихідному просторі є нелінійною. Для використання побудованої функції виконується зворотне перетворення в початковий простір (рис. 6).

Рис. 6. Графічна інтерпретація прямого і зворотного перетворень з лінійного простору в нелінійне

Описаний підхід має один істотний недолік. Процес перетворень досить складний з точки зору обчислень, причому обчислювальна складність зростає із збільшенням числа даних. Якщо врахувати, що перетворення виконується два рази (пряме і зворотне), то така залежність не є лінійною. У зв'язку з цим побудова нелінійних моделей з таким підходом буде неефективним. Альтернативою йому може служити метод Support Vector Machines (SVM), який не виконує окремі перетворення всіх об'єктів, а враховує це в розрахунках.

5.3. Support Vector Machines (SVM)

У 1974 р. вийшла перша книга Вапніка і Червоненкіса "Теорія розпізнавання образів", що поклала початок цілій серії їх робіт у цій області. Запропоновані авторами методи розпізнавання образів і статистична теорія навчання, яка лежить в їх основі, виявилися досить успішними і увійшли в арсенал методів Data Mining. Алгоритми класифікації та регресії під загальною назвою SVM в багатьох випадках успішно замінили нейронні мережі і в даний час застосовуються дуже широко.

Ідея методу ґрунтується на припущенні про те, що найкращим способом поділу точок у -мірному просторі є площина (задана функцією ) рівновіддалена від точок, що належать різним класам. Для двовимірного простору цю ідею можна уявити у вигляді, зображеному на рис. 7.

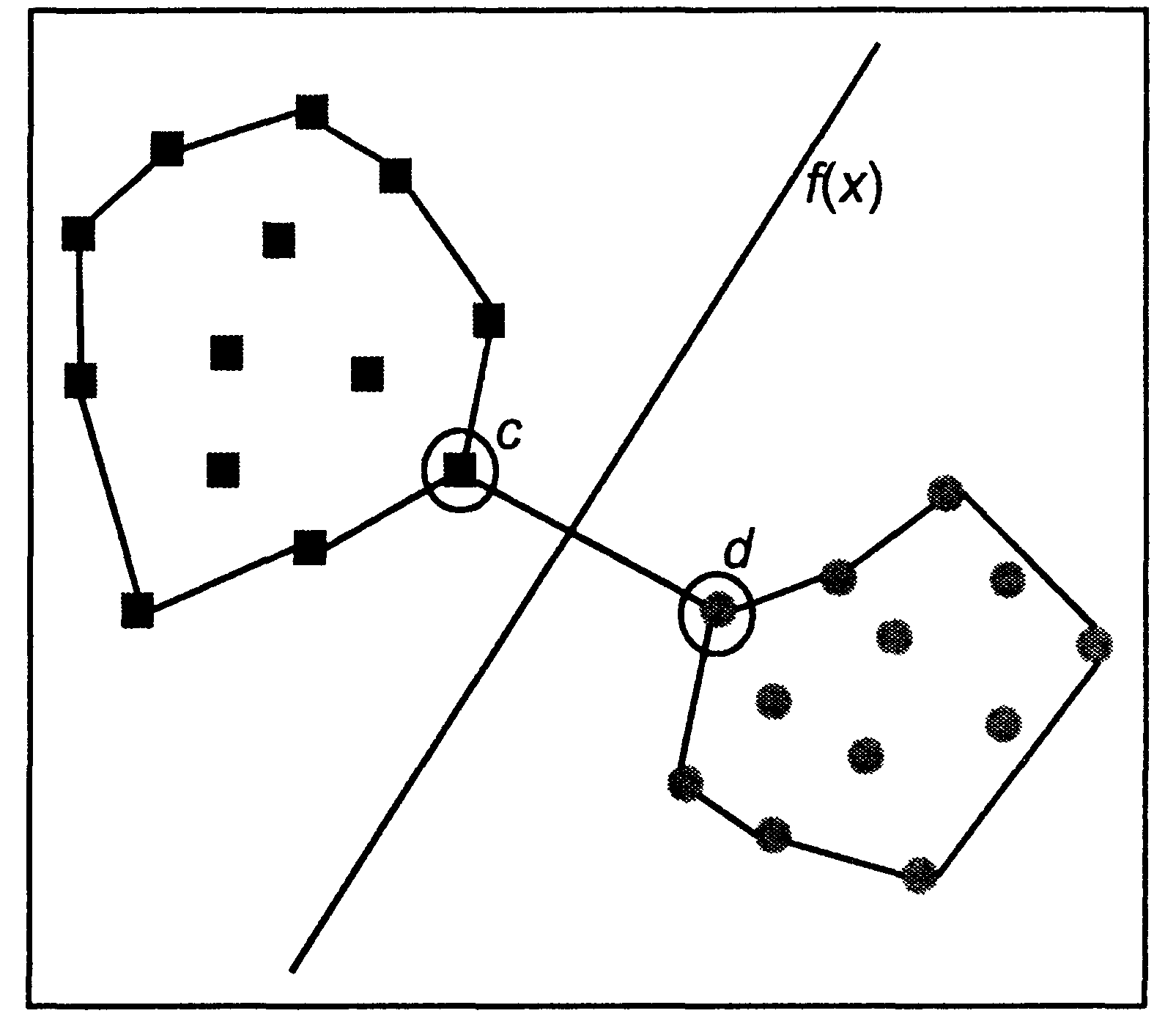
Рис. 7. Графічна інтерпретація ідеї методу SVM

Як можна помітити, для вирішення цього завдання досить провести площину, рівновіддалену від найближчих один до одного точок, що відносяться до різного класу. На малюнку такими точками є точки с і d. Даний метод інтерпретує об'єкти (і відповідні їм у просторі точки) як вектори розміру . Іншими словами, незалежні змінні, що характеризують об'єкти, є координатами векторів. Найближчі один до одного вектори, які відносяться до різних класів, називаються векторами підтримки (support vectors).

Формально це завдання можна описати як пошук функції, відповідає таким умовам:

для деякого кінцевого значення помилки .

Якщо лінійна, то її можна записати у вигляді:

, , ,

де – скалярний добуток векторів і , – константа, що замінює коефіцієнт .

Введемо поняття площини функції таким чином, що більшому значенню площини відповідає менше значення евклідової норми вектора :

.

Тоді задачу знаходження функції можна сформулювати наступним чином – мінімізувати значення за умови:

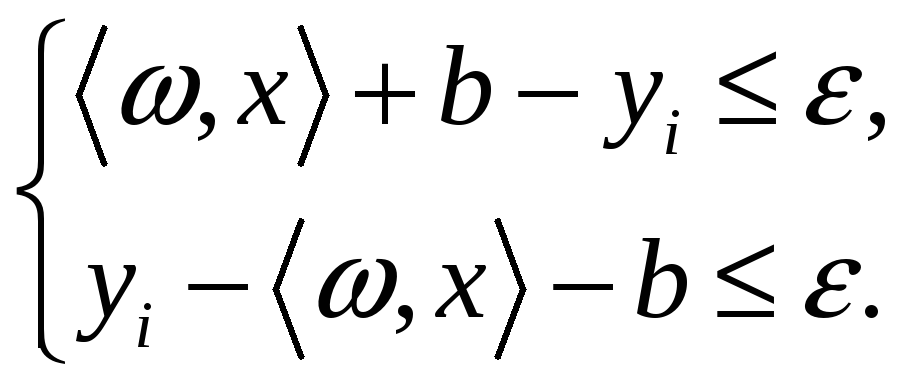
Рішенням цієї задачі є функція виду:

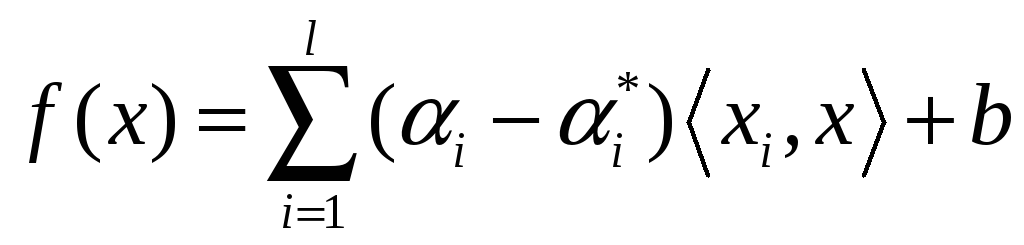, (5.3)

де і – позитивні константи, що задовольняють наступним умовам:

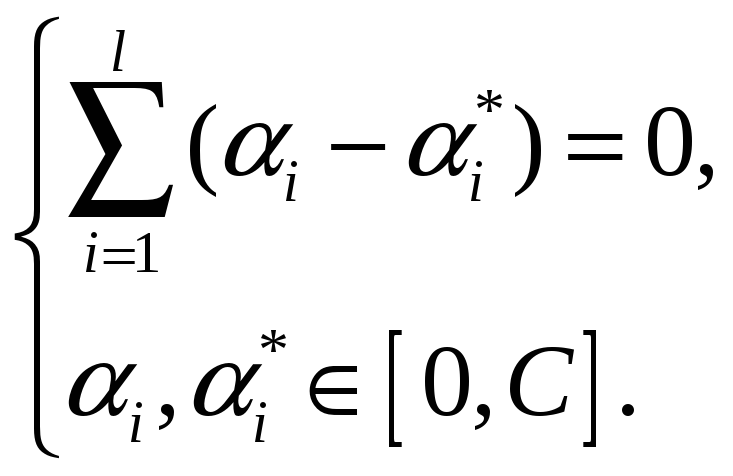
Константа задає співвідношення між площиною функції і допустимими значеннями порушення межі .

Незважаючи на те що розглянутий випадок з лінійною функцією , метод SVM може бути використаний і для побудови нелінійних моделей. Дня цього скалярний добуток двох векторів необхідно замінити на скалярний добуток перетворених векторів:

.

Функція називається ядром.

Тоді вираз 5.3 можна переписати у вигляді:

.

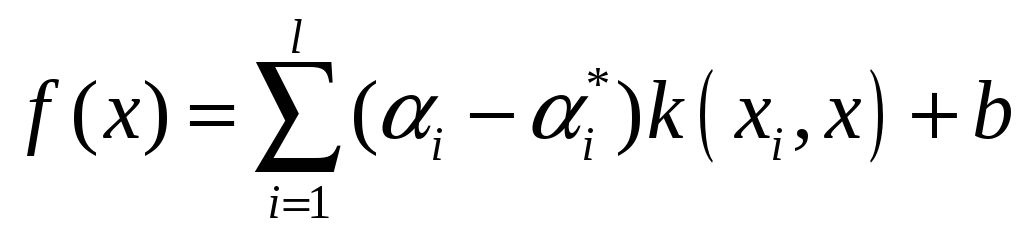Відмінність від лінійного варіанта SVM тут у тому, що тепер знаходиться не безпосередньо, а з використанням перетворення . Необхідно також зауважити, що при створенні нелінійних моделей з використанням методу SVM не виконується пряме, а потім зворотне перетворення об'єктів з нелінійного в лінійний простір. Перетворення закладено в самій формулі розрахунку, що значно знижує обчислювальні витрати.

Вид перетворення, а точніше функція , може бути різного типу і вибирається залежно від структури даних. У табл. 6 наведені основні види функцій класифікації, що застосовуються в SVM-методі.

Таблиця 6

Ядро	Назва
	Лінійна
	Поліном ступеня d
	Базова радіальна функція Гауса
	Сигмоїдальна

До переваг методу SVM можна віднести наступні фактори:

• теоретична і практична обґрунтованість методу;

• загальний підхід до багатьох задач. Використовуючи різні функції 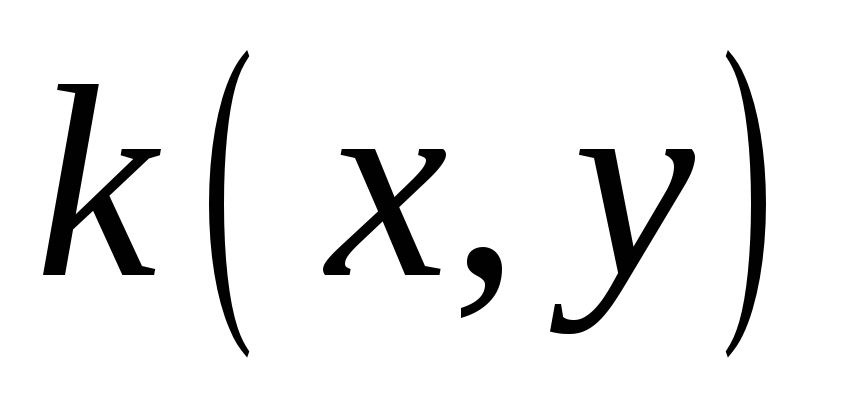, можна одержати рішення для різних задач;

• стійкі рішення, немає проблем з локальними мінімумами;

• не схильний до проблеми overfitting;

• працює за будь-якої кількості вимірювань.

Недоліками методу є:

• невисока продуктивність у порівнянні з більш простими методами;

• відсутність загальних рекомендацій щодо підбору параметрів і вибору ядра;

• побічні ефекти нелінійних перетворень;

• складності з інтерпретацією результату.