4. Методи побудови дерев рішень

4.1. Методика "розподіляй і володарюй"

Загальний принцип – підхід до побудови дерев рішень, оснований на методиці "розподіляй і володарюй", полягає у рекурсивному розбитті множини об'єктів з навчальної вибірки на підмножини, що містить об'єкти, які відносяться до однакових класів.

Щодо навчальної вибірки і множини класів можливі три ситуації:

• множина містить один або більше об'єктів, що відносяться до одного класу . Тоді дерево рішень для – це лист, який визначає клас ;

• множина 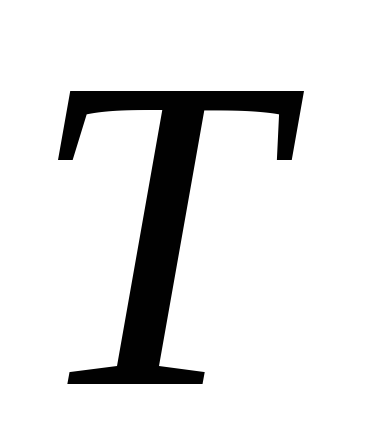не містить жодного об'єкта (порожня множина). Тоді це знову лист, і клас, асоційований з листом, вибирається з іншої множини, відмінної від , наприклад з множини, асоційованої з батьком;

• множина містить об'єкти, пов'язані з різними класами. У цьому випадку слід розбити множину на деякі підмножини. Для цього вибирається одна з незалежних змінних , що має два і більше відмінних один від одного значень ; розбивається на підмножини , де кожна підмножина містить всі об'єкти, що мають значення для обраної ознаки. Ця процедура буде рекурсивно тривати до тих пір, поки в кінцевій множині не будуть об'єкти тільки одного класу.

Очевидно, що при використанні даної методики побудова дерева рішень буде відбуватися зверху вниз. Описана процедура лежить в основі багатьох алгоритмів побудови дерев рішень. Більшість з них є "жадібними алгоритмами". Це означає, що якщо один раз змінна була обрана і по ній було вироблено розбиття на підмножини, то алгоритм не може повернутися назад і вибрати іншу зміну, яка дала б краще розбиття. Тому на етапі побудови не можна сказати, чи дасть обрана змінна в кінцевому підсумку оптимальне розбиття.

При побудові дерев рішень особливу увагу приділяється вибору змінної, по якій буде виконуватися розбиття. Для побудови дерева на кожному внутрішньому вузлі необхідно знайти таку умову (перевірку), яка б розбивала множину, асоційовану з цим вузлом, на підмножини. В якості такої перевірки повинна бути обрана одна з незалежних змінних. Загальне правило для вибору можна сформулювати наступним чином: вибрана змінна повинна розбити множину так, щоб отримані у результаті підмножини складалися з об'єктів, що належать до одного класу, або були максимально наближені до цього, тобто кількість об'єктів з інших класів ("домішок") в кожної з цих множин була мінімальної. Різні алгоритми реалізують різні способи вибору.

Іншою проблемою при побудові дерева є проблема зупинки його розбиття. На додаток до основного методу побудови дерев рішень були запропоновані наступні правила:

• використання статистичних методів для оцінки доцільності подальшого розбиття, так звана рання зупинка (prepruning). У кінцевому рахунку "рання зупинка" процесу побудови приваблива в плані економії часу навчання, але тут доречно зробити одне важливе застереження; цей підхід будує менш точні класифікаційні моделі, і тому "рання зупинка" вкрай небажана. Визнані авторитети в цій галузі Л. Брейман і Р. Квінлен радять буквально наступне: "замість зупинки використовуйте відсікання";

• обмежити глибину дерева. Зупинити подальшу побудову, якщо розбиття веде до дерева з глибиною, що перевищує задане значення;

• розбиття повинно бути нетривіальним, тобто отримані в результаті вузли повинні містити не менше заданої кількості об'єктів.

Цей список евристичних правил можна продовжити, але на сьогоднішній день не існує такого, яке б мало велику практичну цінність. До цього питання слід підходити обережно, тому що деякі з правил остосовні в якихось окремих випадках.

Дуже часто алгоритми побудови дерев рішень дають складні дерева, які "переповнені даними", мають багато вузлів та гілок. У таких "розлогих" деревах дуже важко розібратися. До того ж, розлоге дерево, що має багато вузлів, розбиває навчальну множину на все більшу кількість підмножин, що складаються з дедалі меншої кількості об'єктів. Цінність правила, справедливого, наприклад, для 2-3 об'єктів, вкрай низька, і в цілях аналізу даних таке правило практично непридатне. Набагато краще мати дерево, що складається з малої кількості вузлів, котрим би відповідало велика кількість об'єктів з навчальної вибірки. І тут виникає питання: а чи не побудувати чи всі можливі варіанти дерев, відповідні навчальній множині, і з них вибрати дерево з найменшою глибиною? На жаль, Л. Хайфілем (L. Hyafill) та Р. Рі-вест (R. Rivest) було показано, що ця задача є NP-повною, а, як відомо, цей клас задач не має ефективних методів рішення.

Для вирішення описаної проблеми часто застосовується так зване відсікання гілок (pruning).

Хай під точністю (розпізнавання) дерева рішень розуміється відношення правильно класифікованих об'єктів при навчанні до загальної кількості об'єктів з навчальної множини, а під помилкою – кількість неправильно класифікованих. Припустимо, що відомий спосіб оцінки помилки дерева, гілок і листя. Тоді можна використовувати таке просте правило:

• побудувати дерево;

• відсікти або замінити піддеревом ті гілки, які не призведуть до збільшення помилки.

На відміну від процесу побудови відсікання гілок відбувається знизу вгору, рухаючись з листя дерева, відзначаючи вузли як листя або замінюючи їх піддеревом. Хоча відсіч не є панацеєю, але в більшості практичних завдань дає хороші результати, що дозволяє говорити про правомірність використання подібної методики.

Алгоритм ID3 – розглянемо більш докладно критерій вибору змінної, що використовується в алгоритмах ID3 і С4.5. Очевидно, що повний набір варіантів розбиття описується множиною (кількістю незалежних змінних).

Розглянемо перевірку змінної (в якості перевірки може бути вибрана будь-яка змінна), яка приймає значень . Тоді розбиття з перевірки дасть підмножини при рівному відповідно . Єдина доступна інформація – яким чином класи розподілені в множині і її підмножини, отримані при розбитті. Саме вона і використовується при виборі змінної. У даному випадку існує чотири варіанти розбиття дерева (рис. 2).

Рис. 2. Чотири варіанти початкового розбиття дерева для різних змінних

Нехай – кількість об'єктів з множини , що відносяться до одного і того ж класу . Тоді ймовірність того, що випадково вибраний об'єкт з множини буде належати класу :

.

Так для прикладу, розглянутого в табл. 1, ймовірність того, що в випадково обраний день гра відбудеться, дорівнює 9/14.

Відповідно до теорії інформації оцінку середньої кількості інформації, необхідного для визначення класу об'єкту з множини , дає вираз:

.

Оскільки використовується логарифм з двійковою основою, цей вислів дає кількісну оцінку в бітах. Для даного прикладу:

біт.

Ту ж оцінку, але тільки вже після розбиття множини за , дає наступний вираз:

.

Наприклад, для змінної спостереження оцінка буде такою:

біт.

Критерієм для вибору атрибута буде наступна формула:

.

Цей критерій рахується для всіх незалежних змінних. У даному прикладі:

Gain (спостереження) = 0,247 біт,

Gain (температура) = 0,029 біт,

Gain (вологість) = 0,152 біт,

Gain (вітер) = 0,048 біт.

Вибирається змінна з максимальним значенням Gain (). Вона і буде перевіркою в поточному вузлі дерева, а потім за нею відбувається подальша побудова дерева. Тобто у вузлі буде перевірятися значення по цій змінній і подальший рух по дереву буде відбуватися у залежності від отриманої відповіді. Таким чином, для випадку з визначенням гри буде обрана змінна спостереження.

Такі ж міркування можна застосувати до отриманих підмножин і продовжити рекурсивно процес побудови дерева до тих пір, поки у вузлі не виявляться об'єкти з одного класу.

Так для множини, отриманої при значенні сонячно змінної спостереження, для інших трьох змінних будуть наступні значення:

Gain (температура) = 0,571 біт,

Gain (вологість) = 0,971 біт,

Gain (вітер) = 0,020 біт.

Таким чином, наступною змінною, по якій буде розбиватися підмножина виявиться вологість. Побудоване дерево буде виглядати так, як зображено на рис. 3.

Рис. 3. Розбиття дерева на другій ітерації для підмножини

Одне важливе зауваження: якщо в процесі роботи алгоритму отримано вузол, асоційований з порожньою множиною (жоден об'єкт не потрапив в даний вузол), то він позначається як лист і як рішення листа вибирається клас, що найчастіше зустрічається у безпосереднього попередника даного листа.

Тут варто пояснити, чому критерій повинен максимізуватися. З властивостей ентропії відомо, що максимально можливе значення ентропії досягається в тому випадку, коли всі повідомлення множини рівноймовірні. У даному випадку ентропія досягає свого максимуму, коли частота появи класів у множині Т рівноймовірна. Необхідно вибрати таку змінну, щоб при розбитті по ній один з класів мав найбільшу ймовірність появи. Це можливо в тому випадку, коли ентропія буде мати мінімальне значення і, відповідно, критерій досягне свого максимуму.

Алгоритм С4.5 – розглянутий спосіб вибору змінної використовує алгоритм ID3. Однак він схильний до надчутливості (overfitting), тобто "вважає за кращі" змінні, які мають багато значень. Наприклад, якщо змінна унікально ідентифікує об'єкти, то з огляду на унікальність кожного значення цієї змінної при розбитті множини об'єктів по ній виходять підмножини, що містять тільки по одному об'єкту. Тому що всі ці множини "однооб’єктні", то й об'єкт відноситься, відповідно до одного-єдиного класу, тому

.

Значить критерій приймає своє максимальне значення, і саме ця змінна буде обрана алгоритмом. Однак якщо розглянути проблему під іншим кутом – з точки зору здатності передбачення побудованої моделі, то стає очевидним вся непотрібність такої моделі.

В алгоритмі С4.5 проблема вирішується введенням деякої нормалізації. Нехай суть інформації повідомлення, що відноситься до об'єкту, вказує не на клас, до якого об'єкт належить, а на вихід. Тоді, за аналогією з визначенням , маємо:

.

Це вираз оцінює потенційну інформацію, що отримується при розбитті множини на підмножин.

Розглянемо такий вираз:

.

Нехай цей вираз є критерієм вибору змінної.

Очевидно, що змінна, що ідентифікує об'єкт, не буде високо оцінена критерієм gain ratio. Нехай є класів, тоді чисельник виразу максимально буде дорівнює , і нехай – кількість об'єктів у навчальній вибірці і одночасно кількість значень змінних, тоді знаменник максимально дорівнює . Якщо припустити, що кількість об'єктів свідомо більше кількості класів, то знаменник зростає швидше, ніж чисельник, і, відповідно, значення виразу буде невеликим.

Незважаючи на поліпшення критерію вибору атрибута для розбиття, алгоритм може створювати вузли і листя, що містять незначну кількість прикладів. Щоб уникнути цього, слід скористатися ще одним евристичним правилом: при розбитті множини принаймні дві підмножині повинні мати не менше заданої мінімальної кількості об'єктів (); зазвичай воно дорівнює двом. У разі невиконання цього правила подальше розбиття цієї множини припиняється і відповідний вузол відзначається як лист. При такому обмеженні можлива ситуація, коли об'єкти, асоційовані з вузлом, відносяться до різних класів. В якості вирішення листа вибирається клас, який найбільш часто зустрічається у вузлі, якщо ж прикладів рівна кількість з усіх класів, то рішення дає клас, найбільш часто зустрічається у безпосереднього попередника даного листа.

Розглянутий алгоритм побудови дерев рішень передбачає, що для змінної, що вибирається в якості перевірки, існують всі значення, хоча явно це ніде не затверджувалося. Тобто для будь-якого прикладу з навчальною вибірки існує значення з цієї змінної.

Перше рішення, яке лежить на поверхні, – не враховувати об'єкти з пропущеними значеннями. Слід підкреслити, що вкрай небажано відкидати весь об'єкт тільки тому, що у одній із змінних пропущено значення, оскільки можна втратити багато корисної інформації.

Тоді необхідно виробити процедуру роботи з пропущеними даними.

Нехай – навчальна вибірка і – перевірка за деякою змінною . Позначимо через кількість невизначених значень змінної . Змінимо формули таким чином, щоб враховувати тільки ті об'єкти, у яких існують значення по змінній :

,

.

У цьому випадку при підрахунку враховуються тільки об'єкти з існуючими значеннями змінної .

Тоді критерій можна переписати:

.

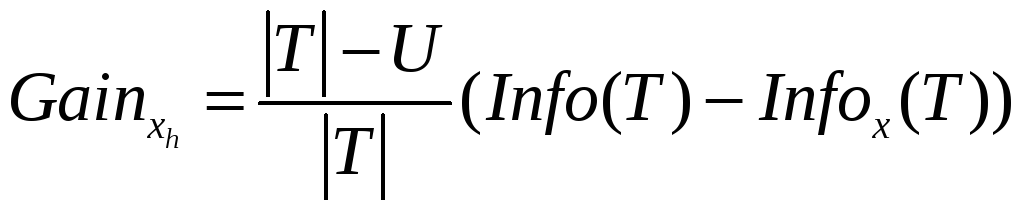Подібним чином змінюється і критерій gain ratio. Якщо перевірка має вихідних значень, то критерій gain ratio розраховується як у випадку, коли вихідна множина поділена на підмножини.

Нехай тепер перевірка з вихідними значеннями вибрана на основі модифікованого критерію.

Необхідно вирішити, що робити з пропущеними даними. Якщо об'єкт з множини Т з відомим виходом асоційований з підмножиною ймовірність того, що приклад з множини дорівнює 1. Нехай тоді кожен об'єкт з підмножини , має вагу, яка вказує ймовірність того, що об'єкт належить . Якщо об'єкт має значення за змінної , тоді вага дорівнює 1, у противному випадку об'єкт асоціюється з усіма множинами з відповідними вагами:

.

Легко переконатися, що:

.

Коротко цей підхід можна сформулювати таким чином: передбачається, що пропущені значення по змінній ймовірнісно розподілені пропорційно частоті появи існуючих значень.

4.2. Алгоритм покриття

Розглянуті раніше методи побудови дерев працюють зверху вниз, розбиваючи на кожному кроці всю навчальну вибірку на підмножини. Метою такого розбиття є отримання підмножин, які відповідають усім класам.

Альтернативою підходу "розділяй і володарюй" є підхід, який полягає у побудові дерев рішень для кожного класу окремо. Він називається алгоритмом покриття, тому що на кожному етапі генерується перевірка вузла дерева, який покриває кілька об'єктів навчальної вибірки.

Ідею алгоритму можна представити графічно (рис. 4). При наявності у об'єктів тільки двох змінних їх можна представити у вигляді точок двомірного простору. Об'єкти, що відносяться до різних класів, відзначаються знаками "+" і "–". Як видно з малюнка, при розбитті множини на підмножини будується дерево, яке покриває тільки об'єкти вибраного класу.

Рис. 4. Геометрична інтерпретація ідеї алгоритму покриття

Для побудови правил за допомогою даного алгоритму в навчальній вибірці повинні бути присутніми всі комбінації значень незалежних змінних. Наприклад, дані, що дозволяють рекомендувати тип контактних лінз, подані в табл. 3.

Таблиця 3

Вік	Припис	Астигматизм	Ступінь зносу	Рекомендації
Юний	Короткозорість	Ні	Знижений	Ні
Юний	Короткозорість	Ні	Нормальний	М'які
Юний	Короткозорість	Так	Знижений	Ні
Юний	Короткозорість	Так	Нормальний	Жорсткі
Юний	Далекозорість	Ні	Знижений	Ні
Юний	Далекозорість	Ні	Нормальний	М'які
Юний	Далекозорість	Так	Знижений	Ні
Юний	Далекозорість	Так	Нормальний	Жорсткі
Літній	Короткозорість	Ні	Знижений	Ні
Літній	Короткозорість	Ні	Нормальний	М'які
Літній	Короткозорість	Так	Знижений	Ні
Літній	Короткозорість	Так	Нормальний	Жорсткі
Літній	Далекозорість	Ні	Знижений	Ні
Літній	Далекозорість	Ні	Нормальний	М'які
Літній	Далекозорість	Так	Знижений	Ні
Літній	Далекозорість	Так	Нормальний	Ні
Старий	Короткозорість	Ні	Знижений	Ні
Старий	Короткозорість	Ні	Нормальний	Ні
Старий	Короткозорість	Так	Знижений	Ні
Старий	Короткозорість	Так	Нормальний	Жорсткі
Старий	Далекозорість	Ні	Знижений	Ні
Старий	Далекозорість	Ні	Нормальний	М'які
Старий	Далекозорість	Так	Знижений	Ні
Старий	Далекозорість	Так	Нормальний	Ні

На кожному кроці алгоритму вибирається значення змінної, яке поділяє всю множину на дві підмножини. Поділ має здійснюватися так, щоб всі об'єкти класу, для якого будується дерево, належали одної підмножини. Таке розбиття проводиться до тих пір, поки не буде побудована підмножина, що містить тільки об'єкти одного класу.

Для вибору незалежної змінної і її значення, яке поділяє множину, виконуються наступні дії:

1. З побудованої на попередньому етапі підмножини (для першого етапу це вся навчальна вибірка), що включає об'єкти, пов'язані з вибраним класом для кожної незалежної змінної, вибираються всі значення, що зустрічаються в цій підмножині.

2. Для кожного значення кожної змінної підраховується кількість об'єктів, що задовольняють цій умові і відносяться до обраного класу.

3. Вибираються умови, що покривають найбільшу кількість об'єктів вибраного класу.

4. Вибрана умова є умовою розбиття підмножини на дві нових.

Після побудови дерева для одного класу таким же чином будуються дерева для інших класів.

Наведемо приклад для даних, поданих в табл. 3. Припустимо, необхідно побудувати правило для визначення умов, при яких необхідно рекомендувати жорсткі лінзи:

якщо (?) то рекомендація = жорсткі.

Виконаємо оцінку кожної незалежної змінної і всіх їх можливих значень:

вік = юний – 2/8;

вік = літній – 1/8;

вік = старий – 1/8;

припис = короткозорість – 3/12;

припис = далекозорість – 1/12;

астигматизм = немає – 0/12;

астигматизм = так – 4/12;

ступінь зносу = низька – 0/12;

ступінь зносу = нормальна – 4/12.

Вибираємо змінну і значення з максимальною оцінкою астигматизм = так. Таким чином, отримуємо уточнене правило такого вигляду:

якщо (астигматизм = так і ?) то рекомендація = жорсткі.

Дане правило утворює підмножину, в яку входять всі об'єкти, що відносяться до класу жорсткі. Крім них у нього входять і інші об'єкти, відповідно, правило повинно уточнюватися (табл. 4).

Таблиця 4

Вік	Припис	Астигматизм	Ступінь зносу	Рекомендації
Юний	Короткозорість	Так	Знижений	Ні
Юний	Короткозорість	Так	Нормальний	Жорсткі
Юний	Далекозорість	Так	Знижений	Ні
Юний	Далекозорість	Так	Нормальний	Жорсткі
Літній	Короткозорість	Так	Знижений	Ні
Літній	Короткозорість	Так	Нормальний	Жорсткі
Літній	Далекозорість	Так	Знижений	Ні
Літній	Далекозорість	Так	Нормальний	Ні
Старечий	Короткозорість	Так	Знижений	Ні
Старечий	Короткозорість	Так	Нормальний	Жорсткі
Старечий	Далекозорість	Так	Знижений	Ні
Старечий	Далекозорість	Так	Нормальний	Ні

Виконаємо повторну оцінку для решти незалежних змінних і їх значень, але вже у новій множині:

вік = юний – 2/4;

вік = літній – 1/4;

вік = старий – 1/4;

припис = короткозорість – 3/6;

припис = далекозорість – 1/6;

ступінь зносу = низька – 0/6;

ступінь зносу = нормальна – 4/6.

Після уточнення отримаємо правило і множину, представлену в табл. 5:

якщо (астигматизм = так і ступінь зносу = нормальна) то рекомендація = жорсткі

Таблиця 5

Вік	Припис	Астигматизм	Ступінь зносу	Рекомендації
Юний	Короткозорість	Так	Нормальний	Жорсткі
Юний	Далекозорість	Так	Нормальний	Жорсткі
Літній	Короткозорість	Так	Нормальний	Жорсткі
Літній	Далекозорість	Так	Нормальний	Ні
Старий	Короткозорість	Так	Нормальний	Жорсткі
Старий	Далекозорість	Так	Нормальний	Ні

Очевидно, що уточнене правило буде мати такий вигляд:

якщо (астигматизм = так і ступінь зносу = нормальна і припис = короткозорість) то рекомендація = жорсткі

Однак в отриманому підмножині відсутній один з об'єктів, відносячи-трудящих до класу жорсткі, тому необхідно вирішити, яке з останніх двох правил більш прийнятно для аналітика.