является то, что они дают только широтную составляющую абсолютных движений, причем более или менее точному измерению поддается только остаточная намагниченность пород, направление которой позволяет судить о палеомагнитной широте литосферной плиты и ее ориентировке относительно полюса (см. раздел 1.5), а данные по палеоклиматической зональности почти всегда крайне приблизительны.

В последние годы делаются попытки реконструировать абсолютные движения плит по следам горячих точек – системы восходящих мантийных струй, поднимающихся с границы ядра и мантии и не смещающихся друг относительно друга в течение длительных по геологическим масштабам интервалов.

Подробнее о горячих точках и мантийных плюмах пойдет речь в разделах 2.5 и 5.3. Здесь же остановимся лишь на роли горячих точек для анализа кинематики плит. Она состоит в том, что литосферная плита, проходя над горячей точкой в мантии, как бы прожигается ею насквозь, и след ее прохождения запечатлевается в виде вулканических поясов, в пределах которых возраст пород закономерно удревняется по простиранию по мере движения от современной вулканической области, т.е. от современного положения горячей точки под литосферной плитой. Простирание вулканического пояса совпадает с направлением прохождения литосферной плиты над горячей точкой и, следовательно, маркирует абсолютное движение плиты по отношению к неподвижной (относительно мантии) системе горячих точек.

К сожалению, физическая природа горячих точек в настоящее время остается не до конца выясненной. Кроме того, пока не доказана и “абсолютная” неподвижность горячих точек как по отношению друг к другу, так и всей системы горячих точек по отношению к оси вращения Земли за длительные геологические интервалы. Приходится признать, что на современном этапе геодинамика достигла больших успехов в анализе относительных перемещений литосферных плит, но пока лишь ищет пути к изучению их абсолютных движений. При этом методы описания кинематики плит, рассматриваемые в данном разделе, едины и не зависят от того, какие движения, относительные или абсолютные, описываются.

2.4.3. Мгновенные и конечные движения

133

Вкинематике плит различаются также мгновенные и конечные движения.

Под мгновенными понимаются движения, происходящие за какой-то крайне ограниченный по длительности промежуток времени. В геологических масштабах за такой промежуток принимается в разных случаях интервал от 1 до 10 млн лет. Следует отметить, что за последние годы, благодаря техническому прогрессу, появилось большое число методов инструментального наблюдения именно мгновенных движений литосферных плит: к ним относятся высокоточные геодезические методы, методы анализа смещений реперных точек земной поверхности из космоса, а также методы решения механизмов землетрясений, происходящих на межплитовых границах.

Вкачестве конечных рассматриваются общие, суммарные движения литосферных плит за любой длительный промежуток времени.

Понятно, что разделение движений плит на мгновенные и конечные во многом условно. Любое конечное движение есть сумма мгновенных, но каждое частное мгновенное движение совсем не обязательно соответствует суммарному конечному по скорости и направлению. Любую точку земной поверхности можно перевести из одного положения в другое (конечное перемещение), строго говоря, бесконечным числом способов (мгновенных перемещений). В то же время любое движение плит, принимаемое за мгновенное, может оказаться суммарным (конечным), т.е. состоящим из серии более мелких мгновенных перемещений.

Наконец, следует иметь в виду, что ключевым параметром анализа любых движений литосферных плит являются возрастные геологические датировки, а точность последних уменьшается в глубь геологической истории. Поэтому один и тот же временной интервал (например, 10 млн лет) будет, скорее всего, рассматриваться как конечный, если изучаются движения плит в кайнозое (последние 60 млн лет земной истории), но этот же интервал наверняка окажется мгновенным, если речь пойдет о кинематике докембрийских литосферных плит (более 600 млн лет назад).

2.4.4.Описание движений плит

134

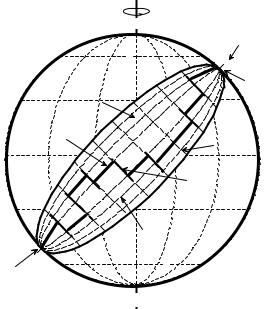
Движения литосферных плит по сфере постоянного радиуса описываются теоремой Эйлера. Она гласит, что перемещение любой точки по поверхности сферы описывается как чистое вращение вокруг оси, проходящей через центр сферы и пересекающей ее поверхность в двух точках, называемых полюсами Эйлера (эйлеровыми полюсами), или полюсами вращения плит

(рис. 2.4.4.1). Надо помнить, что в сферическом пространстве все перемещения являются вращениями, они происходят по дугам окружностей, а кратчайшее расстояние между двумя точками – не прямая, как на плоскости, а дуга большого круга с центром, расположенным в центре сферы. Все другие дуги на поверхности сферы, центр которых находится не в ее центре, называются

малыми кругами.

Чтобы лучше понять невозможность поступательных движений на сферической поверхности, представим себе глобус. Если

нам кажется, что какая-то плита на нем движется поступательно,

135

то на самом деле это означает, что она вращается вокруг удаленного эйлерова полюса. Если же нам, наоборот, кажется, что плита вращается на месте, то эйлеров полюс такой плиты находится близко или даже в пределах самой плиты.

Система вращения любой конкретной литосферной плиты представляет собой два эйлеровых полюса-антипода и связанную с ними систему эйлеровых параллелей и меридианов (см. рис. 2.4.4.1). Такая система подобна географической сетке, но смещена относительно нее, поскольку ось вращения плиты, соединяющая эйлеровы полюса, в общем случае не совпадает с осью вращения Земли. Каждой литосферной плите соответствует своя индивидуальная система вращения. Если рассматриваются две смежные плиты с общей границей, то у них будет общая система вращения, но направление вращения для каждой из смежных плит будет противоположным.

Подобно географической сетке, все эйлеровы меридианы являются большими кругами, а все параллели – малыми кругами, за исключением эйлерова экватора, отстоящего от обоих полюсов на 90°. При этом ориентировка дивергентных границ, где плиты расходятся, в идеале отвечает эйлеровым меридианам, а ориентировка трансформных границ, по которым плиты скользят друг относительно друга, – эйлеровым параллелям.

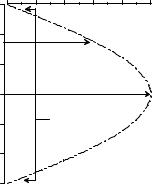
Количественной характеристикой движений плит является угловая скорость вращения ω. Но следует иметь в виду, что при постоянной угловой скорости различные точки вращающейся плиты движутся с разными линейными скоростями V. Чем дальше находится точка плиты от полюса вращения, тем больший путь при повороте на одинаковый угол она будет проходить по сравнению с другими точками той же плиты, расположенными ближе к полюсу вращения и соответственно тем большей будет линейная скорость этой точки. Линейная скорость возрастает пропорционально синусу угла между точкой плиты и полюсом ее вращения (косинусу эйлеровой широты) и достигает максимального значения на эйлеровом экваторе, т.е. на одинаковом расстоянии от эйлеровых полюсов-антиподов (рис. 2.4.4.2).

Таким образом, первая и основная задача кинематики литосферных плит состоит в нахождении по экспериментальным данным о направлениях и линейных скоростях движений плит в разных точках их общей границы главных параметров движения –

136

географических координат эйлеровых полюсов и угловых скоростей вращения.

Задача решается следующим образом. Пусть хотя бы в двух точках межплитовой границы A(ϕ1, λ1) и B(ϕ2, λ2) известны азимуты движения плит α1 и α2 и хотя бы в одной точке – линейная скорость V этого движения. Координаты полюса вращения плит P(ϕ0, λ0) находятся решением системы двух уравнений

где

cos x = sinϕ0 sinϕ1 +cosϕ0 cosϕ1 cos(λ0 −λ1 ), cos y = sinϕ0 sinϕ2 +cosϕ0 cosϕ2 cos(λ0 − λ2 ).

При вычислениях следует помнить, что на сфере существуют два полюса-антипода, расположенных в противостоящих друг другу точках земного шара.

Определив координаты полюса вращения и зная хотя бы одно значение линейной скорости плит V, легко вычислить угловую скорость их вращения

137

здесь ω – угловая скорость, град/год; V – линейная скорость, см/год; R – радиус Земли, км; θ – расстояние (в градусах дуги большого круга) от полюса вращения до точки, в которой измерена линейная скорость; 0,01745 – коэффициент перевода из градусов в радианы.

Угловое расстояние θ между точками с географическими координатами (ϕ1, λ1) и (ϕ2, λ2) вычисляется по формуле

θ = arccos [sinν1 sinν2 cos(λ1 − λ2 ) + cosν1 cosν2 ], (2.4.4.3)

где ν = 90o −ϕ , а линейное расстояние S по дуге большого круга составляет

R – радиус Земли, а θ выражено в радианах.

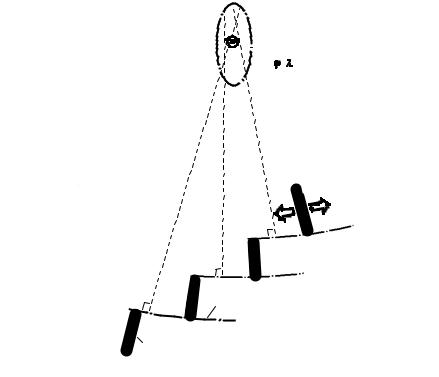
Простой и наглядный способ графического определения полюса вращения двух плит с общей дивергентно-трансформной границей показан на рис. 2.4.4.3. Как уже говорилось, трансформные участки межплитовых границ, по которым вращающиеся плиты скользят друг относительно друга, соответствуют эйлеровым параллелям (дугам малых кругов). Следовательно, если восстановить перпендикуляры к эйлеровым параллелям (т.е. построить эйлеровы меридианы, каждый из которых будет отрезком большого круга), то последние в идеале пересекутся в точке, которая и является искомым полюсом вращения двух плит (эйлеровым полюсом).

Понятно, что экспериментальные данные о движении плит всегда несут в себе какую-то погрешность. Поэтому оптимален статистический способ оценки параметров вращения литосферных плит, при котором вычисления по формулам (2.4.4.1), (2.4.4.2) или геометрические построения (см. рис. 2.4.4.3) проводятся многократно, с использованием серий экспериментальных данных в разных точках межплитовой границы. Достоверность определения полюса в данном случае оценивается эллипсом доверительной вероятности.

Каждому полюсу и, следовательно, каждой паре плит, для которых он получен, соответствует свой эллипс одной и той же доверительной вероятности. Причем доверительная вероятность (критерий качества статистической оценки положения полюса)

138

задается единой для всех анализируемых плит. Например, если используются эллипсы 95%-ной доверительной вероятности, то это означает, что для каждой пары плит можно с вероятностью 95% ожидать нахождения полюса их вращения внутри эллипса.

Линейная

скорость

V

Плита A

Рис. 2.4.4.3. Графическое определение полюса вращения двух плит, разделенных дивергентно-трансформной границей.

При таком подходе площадь эллипса отражает точность определения полюса: чем точнее определены параметры относительного вращения конкретной пары литосферных плит, тем меньше площадь эллипса доверительной вероятности. Отсюда понятно, что если для той же пары плит по той же серии экспериментальных данных найти полюс и оценить точность его нахождения эллипсом не 95%-ной, а, скажем, 60%-ной доверительной вероятности, последний эллипс, естественно, будет иметь меньшую площадь. Но из этого отнюдь не следует, что полюс определен точнее – просто во втором случае уменьшается уверенность в том, что полюс действительно находится внутри эллипса.

139