Практична робота з дисципліни Сучасне компютерне забезпечення Модуль 1 НЕ12
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Чернівецький національний університет імені Юрія Федьковича
Факультет будівництва, архітектури та декоративно-прикладного мистецтва Кафедра будівництва
ВИКОРИСТАННЯ MS EXCEL
ДЛЯ РОЗВ'ЯЗАННЯ ПРИКЛАДНИХ ЗАДАЧ
Методичні вказівки до практичних робіт з навчальної дисципліни «Сучасне комп'ютерне забезпечення»
для студентів спеціальностей: 7.06010101, 8.06010101 «Промислове та цивільне будівництво»
Розглянуто вирішення практичних економічних задач у MS EXCEL з виконанням пошуку параметрів, що забезпечують наперед заданий результат або мінімально чи максимально можливий, за допомогою інструментів: Поиск решения та
Диспетчер сценариев.
Призначено для студентів спеціальностей: 7.06010101, 8.06010101 «Промислове та цивільне будівництво»
1. |
Складання штатного розкладу (1 бал) .................................................................................... |
2 |
2. |
Складання плану вигідного виробництва (1 бал)................................................................... |
3 |
3.Задача визначення витрат на рекламу, при яких прибуток від реалізації товару буде
максимальним (1 бал)...................................................................................................................... |
4 |
4. Задача прогнозування (1 бал) .................................................................................................. |
6 |
5.Планування структури виробництва з врахуванням зменшення норми прибутку при
збільшенні обсягів виробництва (2 бали) ...................................................................................... |
8 |
|
6. |
Задача перевезення вантажів (транспортна задача, 2 бали) .................................................. |
9 |
7. |
Задача керування оборотним капіталом (2 бали) ................................................................. |
10 |
Варіант № 1 завдань для виконання практичної роботи............................................................. |
18 |
|
Варіант № 2 завдань для виконання практичної роботи............................................................. |
20 |
|
Загальні положення
При вирішенні практичних задач виникають ситуації, коли необхідно досягти якоїсь конкретної мети, наприклад, щоб собівартість продукції становила визначену суму. Специфіка таких задач полягає в тому, що в розпорядженні користувача є математична модель досліджуваного процесу, наприклад, закон ціноутворення, але невідомо, при якому значенні вхідного параметра можна досягти поставленої мети.
1
У MS Excel спосіб вирішення подібних задач реалізований як пошук значення параметра формули, що задовольняє її конкретному значенню. Цю процедуру використовують для пошуку такого значення комірки, при якому значення іншої комірки, що обчислюється за формулою, заздалегідь задано. У формулі повинне бути посилання на цільову комірку.
Пошук значення параметра формули, що задовольняє її конкретному значенню, - це чисельне розв'язання рівняння. Іншими словами, використовуючи Excel, можна вирішувати будь-які рівняння з однією змінною.
Розв'язання задач оптимізації у MS Excel
Можливо виконати пошук кількох параметрів, що забезпечують якийсь наперед заданий результат або мінімально чи максимально можливий. Наприклад, мінімізувати витрати на персонал чи максимізувати прибуток від реалізації продукції. Подібні задачі оптимізації в Excel вирішують за допомогою інструменту Поиск решения.
Якщо математична модель досліджуваного процесу й обмеження на значення її параметрів є лінійними, то задача досягнення мети є задачею лінійного програмування. За умови нелінійності математичної моделі процесу чи обмежень на значення параметрів розглядувана задача є задачею нелінійного програмування.
1. Складання штатного розкладу (1 бал)
Вирішення подібних задач розглянемо на прикладі розробки штатного розкладу. Нехай кількість співробітників, необхідна для нормальної роботи установи, знаходиться в деякому діапазоні значень. Загальний місячний фонд зарплати повинний бути мінімальний. Необхідно визначити, якими повинні бути оклади співробітників установи, за умови, що оклад співробітника з мінімальною зарплатою не повинний бути менше 180 грн.
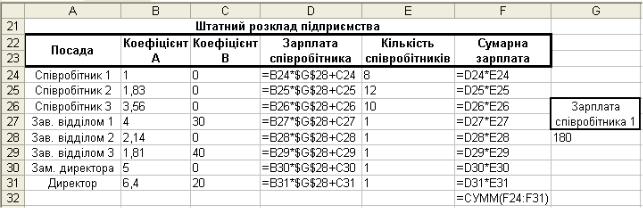
При побудові моделі вирішення задачі за основу береться оклад найбільш низькооплачуваного співробітника, а інші оклади обчислюються, виходячи з визначених коефіцієнтів А і В, тобто кожен оклад є лінійною функцією від окладу співробітника з мінімальною зарплатою. Робочий лист електронної таблиці буде виглядати, як показано на рис. 1.
Рис. 1
2
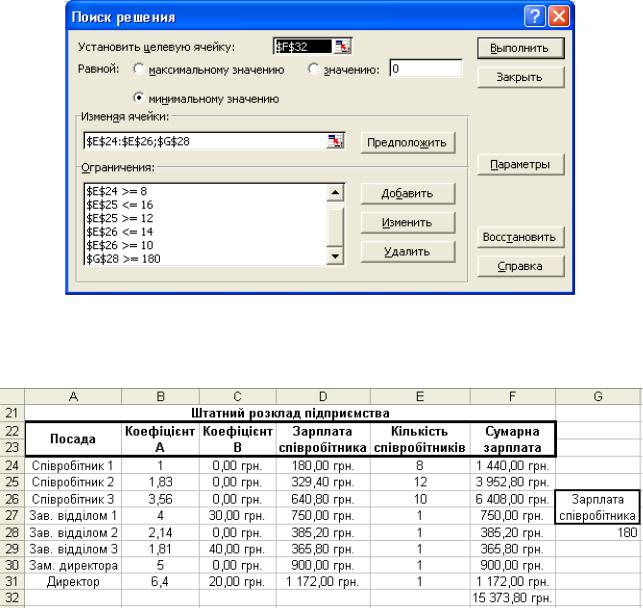
Вирішення задачі виконується з використанням команди Поиск решения з меню Сервис. Вікно Поиск решения показане на рис. 2. Обмеження описують діапазон припустимої кількості співробітників установи і значення найменшого окладу.
Рис. 2
Результати вирішення задачі наведені на рис. 3.
Рис. 3
2. Складання плану вигідного виробництва (1 бал)
Випускається продукція типів "A", "B" і "C". Відомий прибуток від реалізації одиниці продукції. Продукцію можна робити в будь-яких кількостях (збут забезпечений), але запаси сировини обмежені. Необхідно визначити, яку продукцію і якої кількості потрібно випустити, щоб загальний прибуток від реалізації був максимальним. Норми витрат сировини на виробництво одиниці продукції кожного виду задані.
Вихідні дані наведені на рис. 4.
3
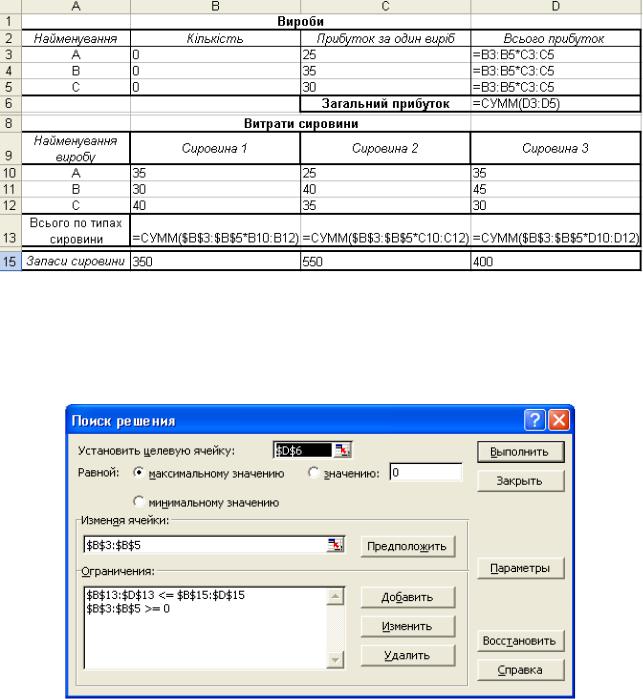
Рис. 4
Задача вирішується за допомогою Поиск решения (рис. 5). Обмеження накладаються на значення комірок, що містять дані про витрати сировини; крім того, кількість виробів не повинна бути від'ємною.
Рис. 5
Розв'язок показує, що оптимальний план випуску передбачає виготовлення 6 одиниць продукції "B" і 4 одиниці продукції "C". Продукцію "А" виробляти не варто. Отриманий прибуток становитиме 339грн.
3. Задача визначення витрат на рекламу, при яких прибуток від реалізації товару буде максимальним (1 бал)
Це типова задача маркетингу. Вирішення цієї задачі дозволяє визначити, чи варто вкладати додаткові кошти в рекламу, щоб збільшити прибуток. Подібні задачі демонструють використання процедури Поиск решения для підбирання таких значень параметрів, що максимізують значення нелінійної функції.
4
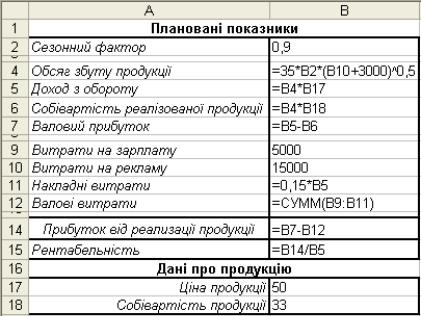
Вихідні дані задачі складаються з 2-х блоків: "Плановані показники" і "Дані про продукцію". Так, у 1-му кварталі заплановані такі показники реалізації: сезонний фактор (СФ) - 0,9; витрати на заробітну плату персоналу -5 тис. грн.; витрати на рекламу (Р) - 15 тис. грн. Дані про продукцію: ціна реалізації - 50 грн.; собівартість продукції - 33 грн. Розрахунок планованих показників роблять з урахуванням того, що: обсяг збуту продукції (З) нелінійно
залежить від сезонного фактора і витрат на рекламу З = 35 . СФ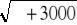 
; доход з обігу визначається як добуток очікуваної кількості проданих одиниць продукції і собівартості продукції; собівартість реалізованої продукції знаходиться, як добуток обсягу збуту продукції на собівартість продукції; валовий прибуток - це різниця доходу з обороту та собівартості реалізованої продукції; накладні витрати фірми обчислюються в обсязі 15% доходу з обороту; валові витрати розраховуються як сума витрат на заробітну плату персоналу, рекламу і накладні витрати; прибуток від продукції визначається як валовий прибуток мінус валові витрати; рентабельність знаходиться, як відношення прибутку від реалізації продукції до доходу з обороту. Дані для пошуку максимуму в задачі маркетингу показані на рис. 6.
Рис. 6
Після активізації Сервис, Поиск решения задається, що комірка Прибуток від реалізації продукції містить цільову функцію; мета оптимізації - Максимальне значення;
при виконанні пошуку найкращого рішення змінюються витрати на рекламу. При призначенні параметрів указується нелінійність моделі. Для інших параметрів використовуються установки за умовчанням, що підходять для вирішення більшості задач.
Результат оптимізації прибутку від реалізації товару в задачі маркетингу показаний на рис. 7. Як видно з отриманого рішення, при витратах на рекламу 19 388 грн. прибуток від реалізації товару буде максимальний, видно, що витрати на рекламу більше запланованих. Однак слід зазначити, що максимізація прибутку не обов'язково відповідає найвищому значенню рентабельності: її значення зменшилося до 9 %.
5
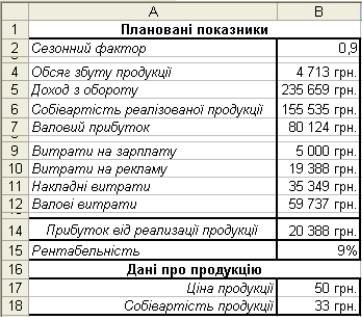
Рис. 7
Вирішимо попередню задачу за умови, що витрати на рекламу не можуть перевищувати 15 000 грн. Розв'язок задачі - 20 149 грн. При цьому зростає рентабельність до
10%.
4. Задача прогнозування (1 бал)
Основою прогнозування є спостереження. Точніше, не самі спостереження, а числові значення деяких станів явища, що спостерігається. Наприклад, курс цінних паперів. Фіксуючи значення курсу в часі, ми одержимо табличний опис процесу зміни курсу. Якщо описати аналітично цей процес, тобто поставити йому у відповідність деяку функціональну залежність, то прогноз буде значенням функції у якийсь наперед заданий момент часу.
Визначимо, скільки можна заробити, придбавши 10 акцій підприємства, якщо задані коливання курсу акцій. Підраховуємо вартість 10 акцій на підставі їхнього відомого курсу (рис. 8), далі будуємо діаграму залежності вартості акцій від декади, апроксимуємо отриману криву за допомогою поліноміальної ступінної залежності. Для цього з контекстного меню діаграми обирається команда Добавить линию тренда. Виберемо як тип лінії тренда поліноміальну апроксимацію 6-го ступеня.
6
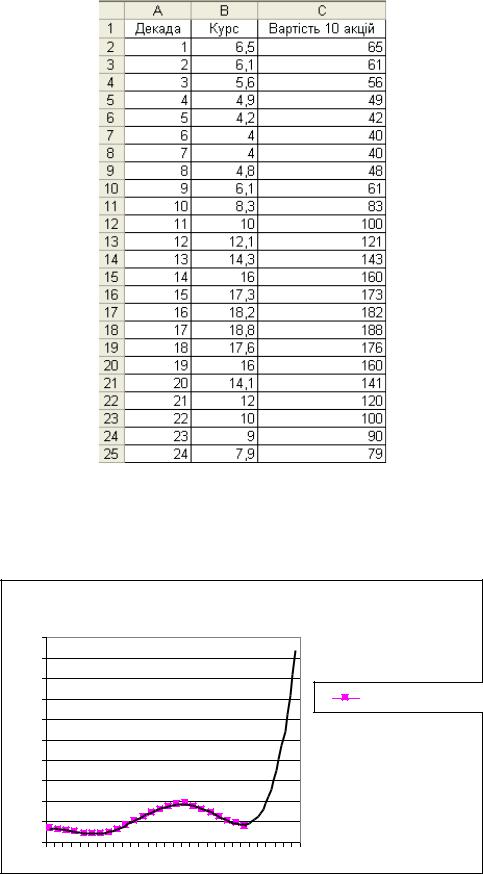
Рис. 8
Результат апроксимації та апроксимуюча функція показані на рис. 9. На вкладці
Параметри задаємо Прогноз вперед на 6 периодов.
|
|
y = 9E-07x6 + 0,0012x5 - 0,0741x4 + |
|||||||
|
1,4678x3 - 10,35x2 + 21,583x + 51,025 |
||||||||
1000 |
|
|
|
|
|
|
|
|
|
900 |
|
|
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
700 |
|
|
|
|
|
|
|
|
Вартість 10 акцій |
600 |
|
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
28 |
Рис. 9
Одержуючи з графіка прогнозне значення вартості акцій і знаходячи різницю між прогнозним значенням і реальним у задану декаду, можна передбачити розміри доходу від покупки акцій.
7
5.Планування структури виробництва з врахуванням зменшення норми прибутку при збільшенні обсягів виробництва (2 бали)
Підприємство випускає телевізори, стерео- і акустичні системи, використовуючи загальний склад комплектуючих. У зв'язку з обмеженістю запасу необхідно знайти оптимальне співвідношення обсягів випуску виробів. Варто враховувати зменшення питомого прибутку при збільшенні обсягів виробництва у зв'язку з додатковими витратами на збут (зменшення коефіцієнта віддачі).
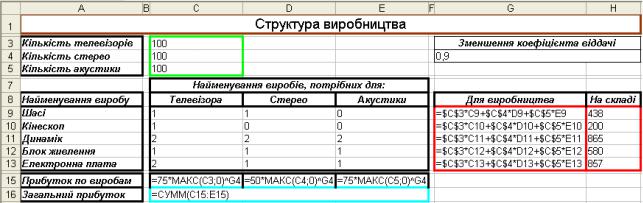
Задача включає дані по кількох виробах (рис. 10), у яких використані загальні комплектуючі, кожному з виробів відповідає своя норма прибутку (НП). Запас комплектуючих обмежений і задача зводиться до визначення кількості кожного виду виробів (КВ) для одержання найбільшого прибутку, що обчислюється, як сума прибутків по виробах
(П).
Рис. 10
У формулу прибутку по виробах П = НП . КВ0,9 входить піднесення до степеня з показником 0,9, що враховує зменшення прибутку з ростом обсягу (зменшення коефіцієнта віддачі). Це робить задачу нелінійною. Зміна показника на 1,0 означає, що прибуток не залежить від обсягу виробництва. Подібна задача є лінійною.
Для вирішення задачі використовується Поиск решения (рис. 11). Мета - одержання найбільшого прибутку. Змінювані дані - кількість виробів кожного виду, що випускаються. Обмеження показують, що кількість використаних комплектуючих не повинна перевищувати їхнього запасу на складі, і кількість виробів, що випускаються, повинна бути додатною.
8
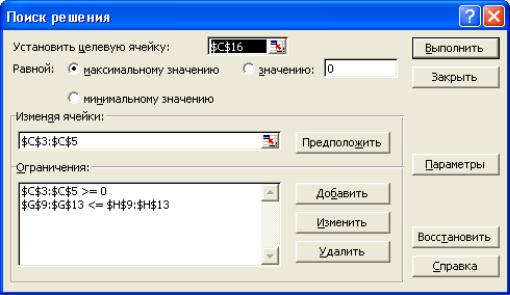
Рис. 11.
Розв'язок показує, що оптимальний план випуску з отриманням максимального прибутку передбачає виготовлення 200 телевізорів, 4 стереота 229 акустичних систем. Прибуток по виробах становитиме відповідно 8 830,56 у. о., 172,67 у. о. і 9 956,85 у. о., загальний прибуток: 18 960,07 у. о.
6. Задача перевезення вантажів (транспортна задача, 2 бали)
Розглянемо задачу доставки товарів із трьох заводів на п'ять регіональних складів (рис. 12). Товари можуть доставлятися з будь-якого заводу на будь-який склад, вартість доставки на більшу відстань буде більшою. Потрібно визначити обсяги перевезень між кожним заводом і складом відповідно до можливостей складів і заводів, при яких транспортні витрати мінімальні. При вирішенні задачі потрібно мінімізувати витрати на перевезення товарів від підприємств-виробників на торгові склади. При цьому необхідно врахувати можливості постачання кожного з виробників при максимальному задоволенні запитів споживачів.
Вартість перевезення у кожне місто визначається, як сума добутків витрат на перевезення на кількість перевезень.
Використовується Поиск решения. Мета - мінімізація всіх транспортних витрат (C19), змінювані дані - обсяги перевезень від кожного з заводів до кожного складу (C4:G6). Обмеження показують, що кількість перевезених вантажів не може перевищувати виробничих можливостей заводів (I4:I6<=I13:I15), кількість доставлених вантажів не повинна бути менше потреб складів (C8:G8>=C10:G10), і також число перевезень не може бути від'ємним (C4:G6>=0). Найшвидше одержати розв'язок даної задачі можна, якщо вибрати використання лінійної моделі перед початком пошуку рішення. Для задачі такого виду оптимальне ціле рішення для цілих значень обсягів перевезень виходить, якщо задані обмеження - також цілі числа.
9
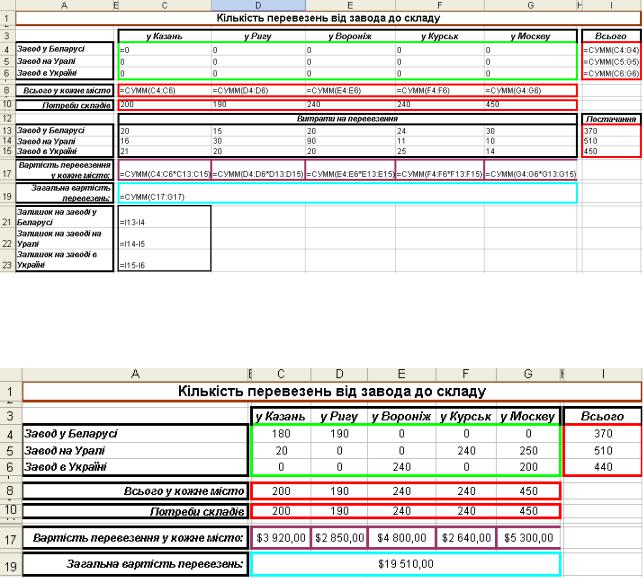
Рис. 12
Результати оптимізації при вирішення транспортної задачі представлені на рис. 13.
Рис. 13
7. Задача керування оборотним капіталом (2 бали)
Потрібно з найбільшою прибутковістю розмістити додатковий капітал в 1-, 3- і 6- місячних депозитах, з огляду на власні потреби в капіталі і гарантійному резерві. Однією з задач співробітника фінансового відділу є короткострокові вкладення з максимальним прибутком при збереженні достатнього резерву для покриття витрат. Більш прибутковими є довгострокові депозити, однак короткострокові депозити надають більш гнучкі можливості керування фінансовими засобами. У даній задачі кінцева сума розраховується з використанням початкової суми (з минулого місяця), плюс депозити, що погашаються, мінус нові депозити і з урахуванням щомісячних потреб самого підприємства (рис. 14).
10