
132 / sam_rob_3
.doc“Прості цикли”
-
Дано натуральне число
 .
Обчислити:
.
Обчислити:
-
Дано дійсне число
 ,
натуральне число
,
натуральне число
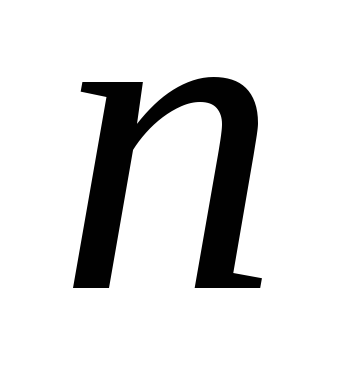 .
Обчислити:
.
Обчислити:
-
Дано дійсне число
 .
Обчислити:
.
Обчислити:
![]()
-
Дано дійсні числа
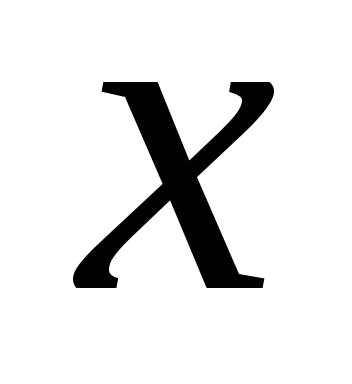 ,
,
 ,
натуральне число
,
натуральне число
 .Обчислити:
.Обчислити:
![]()
-
Дано дійсне число
 .
Знайти:
.
Знайти:
-
серед чисел
 ,
,
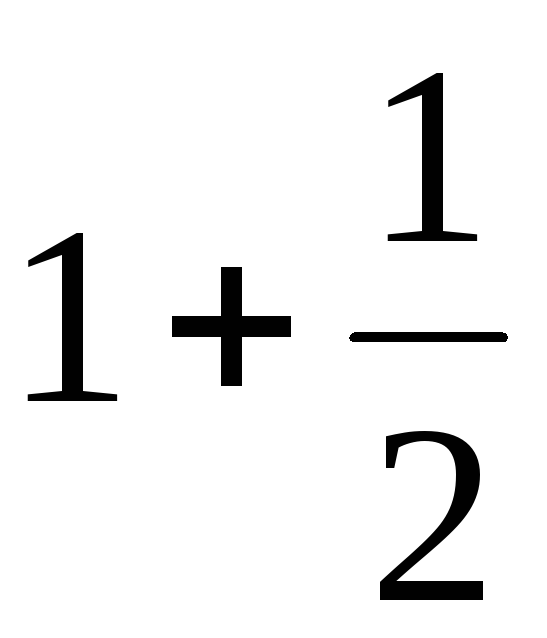 ,
,
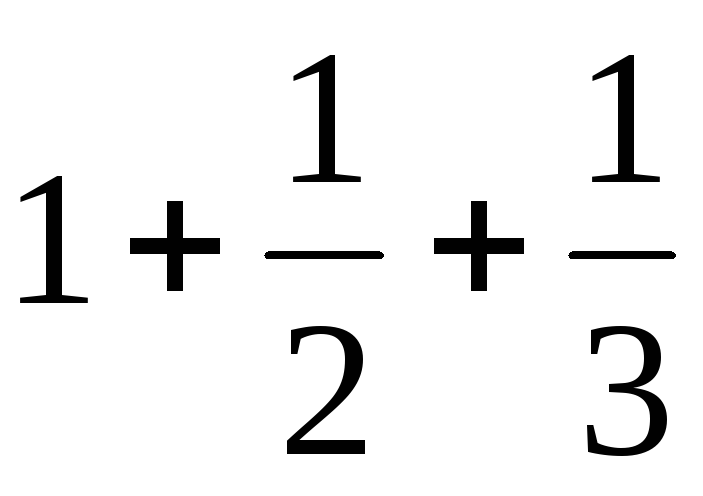 ,
… перше, більше за а
,
… перше, більше за а -
таке найменше
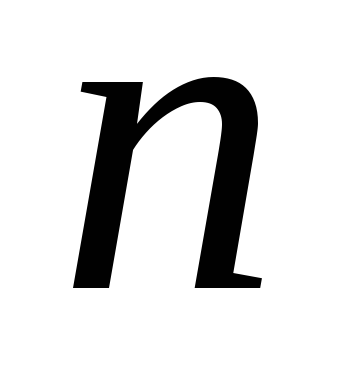 ,
що
,
що

-
Дано натуральне
 .
.
-
Скільки цифр в числі
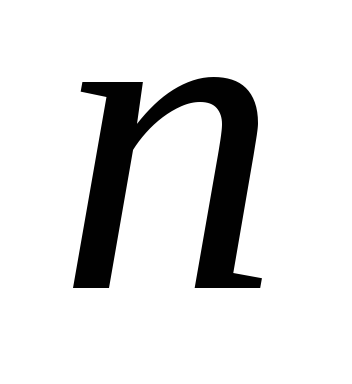 ?
? -
Чому дорівнює сума його цифр?
-
Знайти першу цифру числа
 .
. -
Знайти знакозмінну суму цифр числа
 .
.
-
Дано натуральні числа
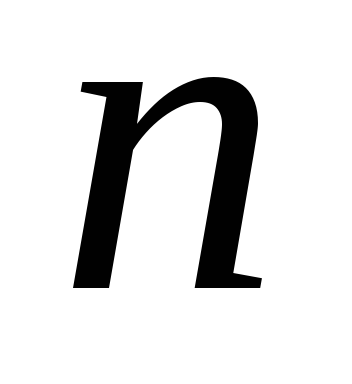 ,
,
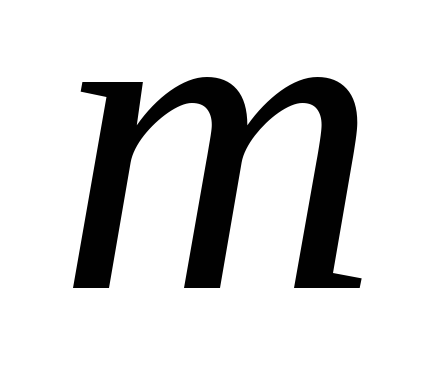 .
Отримати суму
.
Отримати суму
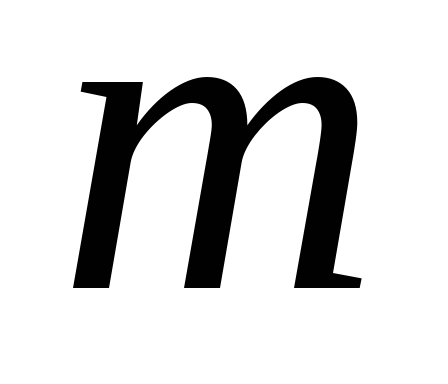 останніх цифр числа
останніх цифр числа
 .
. -
Дано натуральне число
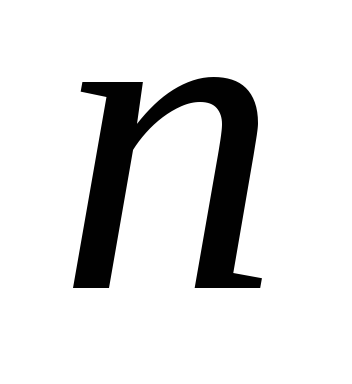 .
.
-
Визначити, чи входить цифра 3 в запис числа
 .
. -
Змінити порядок цифр числа
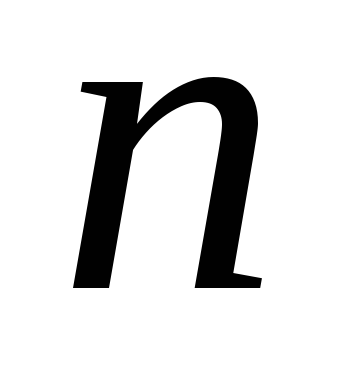 на обернений. Визначити чи є воно
паліндромом.
на обернений. Визначити чи є воно
паліндромом. -
Переставити першу і останню цифри числа
 .
. -
Приписати по одиниці в початок і в кінець запису числа
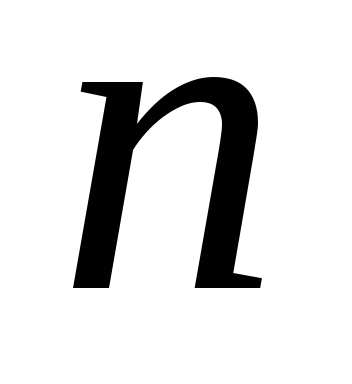 .
. -
Обчислити і надрукувати середнє арифметичне цифр у записі цього числа.
-
Дано натуральні числа
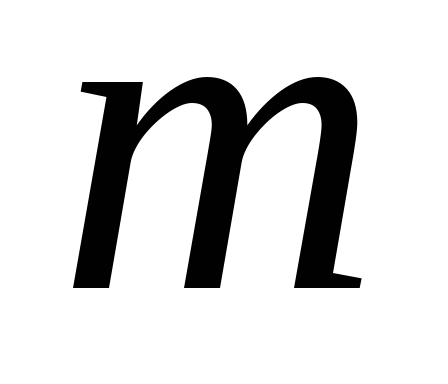 і
і
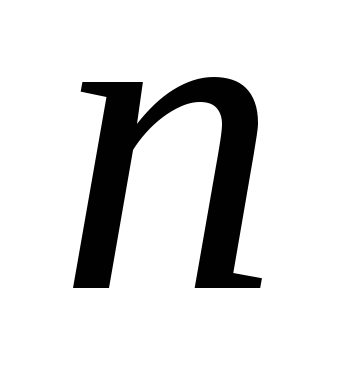 .
Знайти такі натуральні
.
Знайти такі натуральні
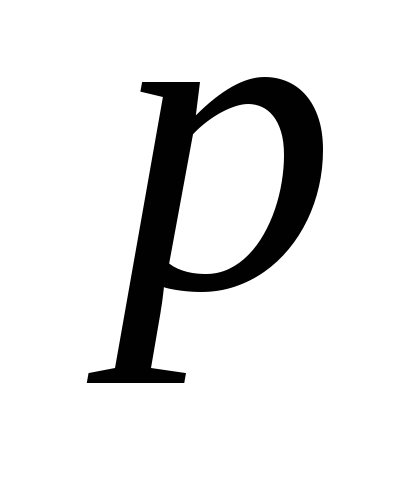 і
і
 ,
що не мають спільних дільників, що
,
що не мають спільних дільників, що
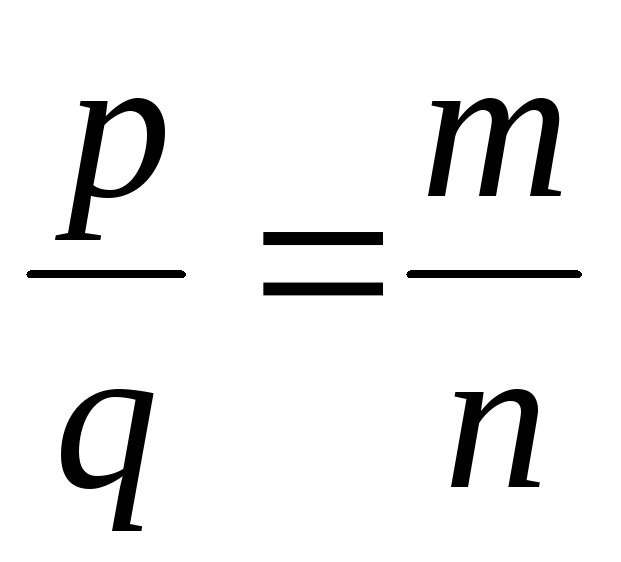 .
. -
Нехай
 ;
;
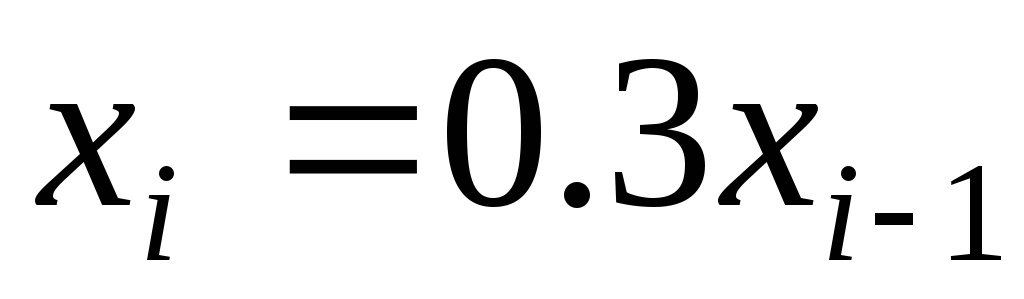 ;
;
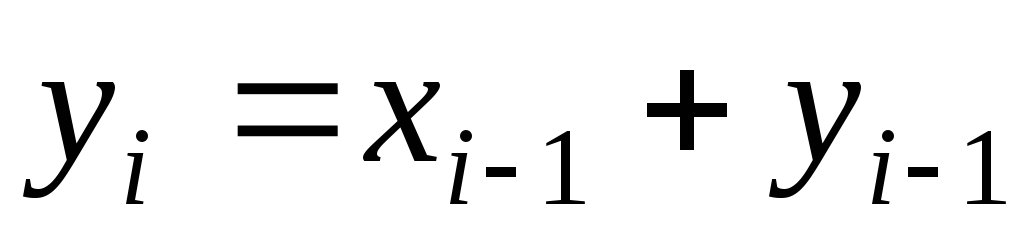 ;
;
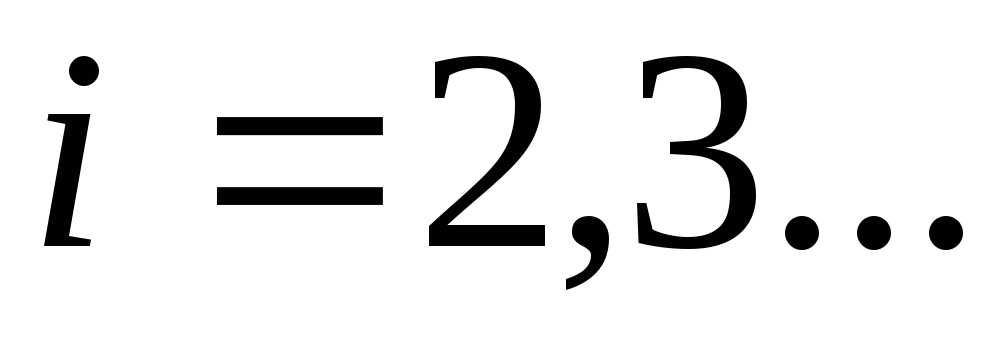 .
.
Дано
натуральне
![]() .
Знайти:
.
Знайти:
![]()
-
Нехай
 ;
;
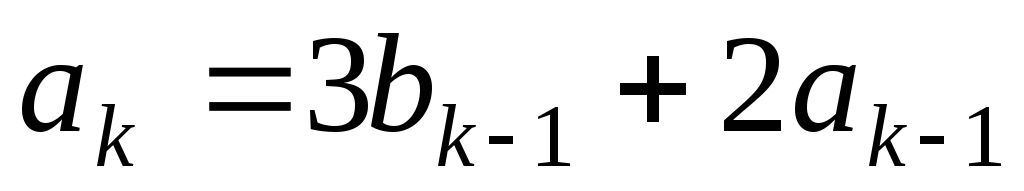 ;
;
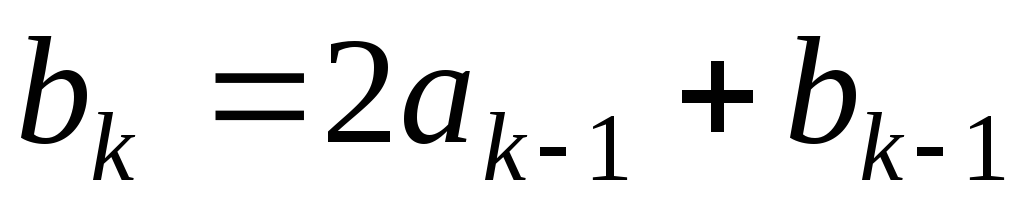 ,
,
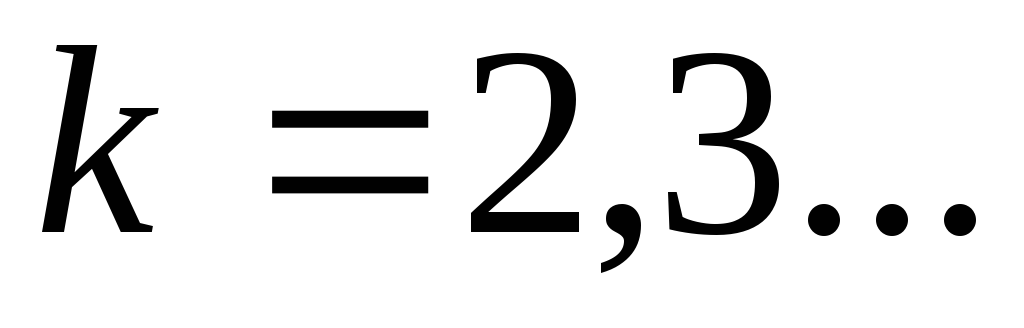 .
.
Дано
натуральне
![]() .
Знайти:
.
Знайти:
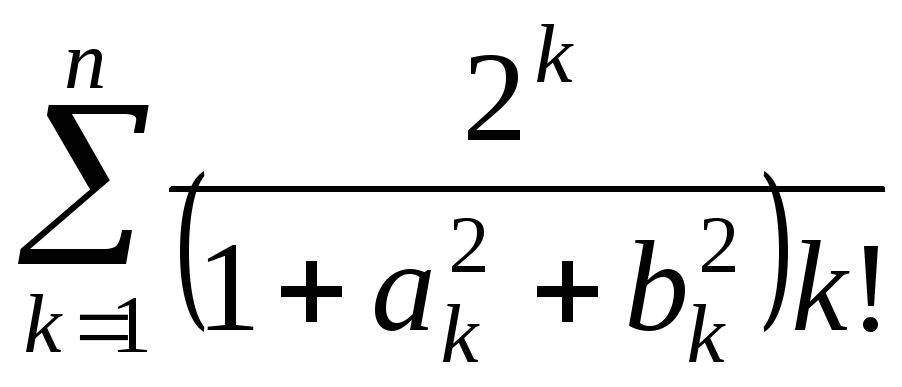
-
Дано натуральне число
 .
Обчислити (одним циклом)
.
Обчислити (одним циклом)
![]() .
.
-
Дано дійсне число
 .
Обчислити:
.
Обчислити:

-
Дано натуральні числа
 Перевірити, чи виконується гіпотеза
Безу для кожного натурального числа з
проміжку
Перевірити, чи виконується гіпотеза
Безу для кожного натурального числа з
проміжку
 не
більше ніж за
не
більше ніж за
 кроків
процесу.
кроків
процесу.
Розглянемо
деяке натуральне число
![]() .
Якщо воно не паліндром, то побудуємо
нове число, змінивши порядок цифр у
записі
.
Якщо воно не паліндром, то побудуємо
нове число, змінивши порядок цифр у
записі
![]() на обернений,
і додамо його до
на обернений,
і додамо його до
![]() .
Якщо отримана сума не паліндром, то
повторимо з нею описані дії, поки не
отримаємо паліндром. Гіпотеза Безу
стверджує, що описаний процес скінчений
для будь-якого натурального
.
Якщо отримана сума не паліндром, то
повторимо з нею описані дії, поки не
отримаємо паліндром. Гіпотеза Безу
стверджує, що описаний процес скінчений
для будь-якого натурального
![]() .
Цю гіпотезу досі не доведено.
.
Цю гіпотезу досі не доведено.
-
Дано натуральне число. Отримати його запис у двійковій системі числення.
-
Дано натуральне
 і дійсні числа
і дійсні числа
 .
Обчислити
.
Обчислити
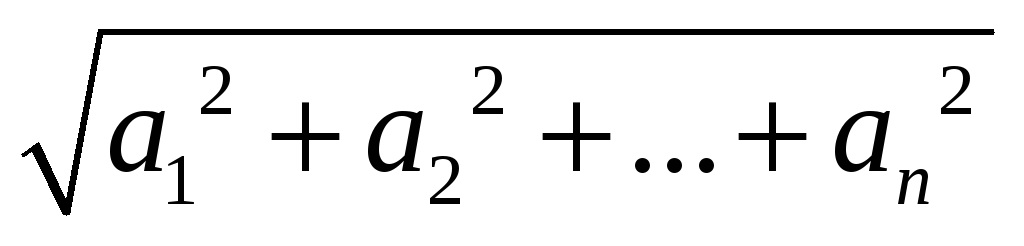 .
.
