Задачи 1-10

• Определить реакции шарнирно-подвижной и шарнирно-неподвижной опор балки, нагруженной силой F, распределенной нагрузкойq и парой с моментом М. Весом балки пренебречь.

К решению этих задач следует приступать после изучения тем «Плоская система произвольно расположенных сил», «Моменты сил», изучения приведенных ниже методических указаний и примеров.

Во всех задачах определению подлежат реакции в опорах балки, находящейся в равновесии под действием плоской системы произвольно расположенных сил. В качестве опор выбраны шарниры. Вид применяемой системы трех уравнений равновесия может быть различным:

• Два уравнения моментов сил и одно уравнение проекций сил;

• Одно уравнение моментов сил и два уравнения проекций сил.

Выполнять проверку обязательно.

Момент силы относительно точки равен нулю в том случае, когда линия действия силы проходит через эту точку. Знак момента пары или силы относительно точки определяется направлением возможного поворота тела вокруг этой точки. Обычно принимают следующее правило:

►знак «+» ставят по ходу часовой стрелки, знак «-» ставят при повороте против хода часовой стрелки.

Последовательность решения задач:

1. изобразить балку вместе с нагрузками;

2. выбрать систему координатных осей, совместив ось ось X с балкой, а ось У направив перпендикулярно оси X;

3. освободить балку от опор, заменив их действие реакциями опор;

4. составить уравнения статического равновесия для произвольной плоской системы сил;

5. проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.

48

Дано: F=20 кН; q=l кН/м; М=10 кНм.

Определить: R_X;R_АУ; R_DУ.

Решение:

Рассматриваем равновесие балки АD. К ней приложены активная сила F и момент М. Рассматривая тело АD как свободное, отбрасываем связи (шарнирные опоры A и D), заменяя их действие реакциями. Реакцию шарнирно – неподвижной опоры А раскладываем на две составляющие R_АУ и R_АХ. Для шарнирно – подвижной опоры D показываем составляющую реакции R_DУ. Для получения плоской системы произвольно расположенных сил составляем три уравнения равновесия, выбрав в качестве центра моментов точки А и D. Равномерно распределенную нагрузку q заменяем заменяем ее равнодействующей Q = q·CD = 1·2 = 2 кН.

Для получения плоской системы произвольно расположенных сил составляем четыре уравнения равновесия, выбрав в качестве центра моментов точки А и D:

1. Σ Х = 0

R _АХ - F · cosα= 0

R _АX = F · cosα= 20 · cos30^o = 20 ·0,866 = 17,3кН;

2. Σm_А(F_i) = 0

F · cos 60^О· АВ + М + Q · AK - R_DУ · AD = 0

R_DУ = = =6,5 кН;

3. Σm_D(F_i) = 0

R_АУ · AD - F ·cos 60^o·BD + M – Q · KD = 0

R_АУ === 5,5 кН;

Проверка:

4.Σ У = 0

R_АУ - F_У – Q + R_DУ = 0

5,5 - 10 - 2 + 6,5 = 0

0=0

Проверка выполнена. Задача решена правильно.

Ответ:R_X = 17,3 кН;R_DУ = 6,5 кН;R_АУ = 5,5 кН.

49

Задачи 11-20

К решению этих задач следует приступать после изучения разделов «Кинематика», «Динамика», изучения приведенных ниже методических указаний и примеров.

• Прямолинейное движение точки задано уравнением S = 2t³ + 2t² + 5, где S выражено в метрах, t – в секундах. Найти скорость и ускорение точки в начальный момент времени и в конце первой и второй секунд.

Дано:S = 2t³ + 2t² + 5

Определить: v_t=0;v_t=1 ; v_t=2 ; а_t=0 ; а_t=1 ; а_t=2 .

Решение:

Определяем скорость движения точки как первую производную от расстояния по времени

V = = 6t² + 4t.

Определяем скорость точки в моменты времени:

t = 0; t = 1с; t = 2с.

v_t=0 = 0; v_t=1 = 6·1² + 4·1 = 10 м/с;v_t=2 = 6·2² + 4·2 = 32 м/с.

Определяем ускорение точки как первую производную от скорости по времени или вторую производную от расстояния по времени:

а = = =12t + 4.

Определяем ускорение точки в момент времени:

t = 0; t = 1с; t = 2с.

а_t=0 = 4м/с²; а_t=1 = 12·1+ 4 = 16 м/с²; а_t=2 = 12·2 + 4 = 28 м/с².

Ответ:v_t=0 = 0; v_t=1 = 10 м/с;v_t=2 = 32 м/с; а_t=0 = 4 м/c²; а_t=1 = 16 м/с²; а_t=2 = 28м/с².

• Поезд движется со скоростью 80 км/ч. При подъеме в гору он движется равнозамедленно и в течение 0,75 мин проходит 750м. Определить скорость поезда в конце подъема пути и величину замедления.

Дано: v = 80 км/ч = 22 м/с; t = 0,75 мин = 45 с; S = 750 м

Определить: a - ? V - ?

Решение:

Пишем уравнение для равнопеременного движения: S = v₀t + .

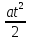Подставляем исходные данные в это уравнение и определяем величину замедления

50

750 = 22·45 + 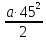=>а = - 0,236 м/с².

Из уравнения скорости для равнопеременного движения определяем скорость поезда в конце подъема:

V = V_o + аt; =>V = 22 – 0,236 ·45 = 11,38 м/с.

Ответ: v = 11, 38 м/с; a = - 0, 236 м/с².

• Тело вращается вокруг неподвижной оси так, что точка А, отстоящая от оси вращения на расстоянии r = 0,6 м, движется по своей траектории по закону

S = 6t + 2t², где S – в метрах, а t – в секундах. Найти для момента времени t = 3 с величину угловой скорости и углового ускорения.

Дано: S = 6t + 2t²;t = 3 с; r = 0,6 м

Определить: w -?; ε -?

Решение:

Определяем закон изменения скорости точки:

V = == 6+ 6t².

Скорость точки в момент времени t = 3с:

V_t=3 = 6 + 6·3² = 60м/с.

Угловая скорость тела: w = ==100 рад/с.

Закон изменения ускорения точки:

а_τ = ==12t.

Касательное и угловое ускорение точки в момент времени t = 3с:

а_τ= 12·3 = 36 м/с; ε = == 60 рад/с.

Ответ: w = 100 рад/с; ε = 60 рад/с.

• Двигатель при пуске в ход достигает за 40 секунд угловой скорости, равной 720 об/мин. Считая вращение в период пуска равноускоренным, найти угловое ускорение двигателя и число его оборотов за эти 40 секунд.

51

Дано: t = 40 с; w = 720 об/мин;

Определить: ε - ?k - ?

Решение:

Выразим угловую скорость в рад/с: w = = = 24π = 75,39 рад/с.

Определяем величину углового ускорения из формулы: w =εt.

ε = = =0,6π = 1,88 рад/с.

Определяем угловое перемещение:

φ = = =480π = 1507,96 рад.

Зная, что один оборот, измеренный в радианах, выражается отвлеченным числом 2π, получим:

k = = = 240 об.

Ответ: ε = 1,88 рад/с; k = 240 об.

• Лифт, поднимаясь равноускоренно, проходит за t = 6 секунд расстояние S = 36 метров. Определить давление на дно лифта человека, массой m = 75 кг.

Дано: t = 6 с; S = 36 м; m = 75 кг; G = 10 м/с

Определить: ε - ?N- ?

Решение:

На лифт действуют следующие силы: сила тяжести человека G, направленная вертикально вниз и реакция пола лифта N, направленная вертикально вверх. Фиктивную силу F_и, равную по величине m·a, направляем противоположно ускорению, т.е.вертикально вниз. Пользуясь принципом Даламбера (методом кинетостатики), считаем силы, действующие на лифт, условно взаимно уравновешенными, проектируя их на ось ОУ:

ΣХ = 0 => N – G – F_и = 0 => N = G + F_и.

Из уравнения равноускоренного движения определяем ускорение:

а ===2 м/с.

52

F_и = m·a = 75 · 2 = 150 Н;

N = 750 + 150 = 900 Н

Ответ: N = 900 Н.

• Поезд идёт по горизонтальному участку пути со скоростью 72 км/ч. Машинист, заметив опасность, выключает ток и начинает тормозить поезд. Сопротивление движению от торможения и трения в осях и о воздух составляет 0,1 от силы тяжести поезда. Определить, какой путь пройдёт поезд от начала торможения.

Дано: v₀ = 72 км/ч = 20 м/с; F = 0,1 G.

Определить: S -?

Решение:

Применяем уравнение кинетической энергии: W = F·S = –.

Так как поезд должен остановиться при v₀ = 0, тогда

F· S = - .

Здесь работу производит сила трения, т.е. W = -0,1GS, выразив силу тяжести через массу, получим: W = -0,1 GS = -0,1 mgS=>

-0,1 mgS = .

Отсюда получим:

S = 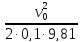= =204м.

Ответ: S = 204 м.

53

• Вычислить мощность турбогенераторов на станции трамвайной сети, если число вагонов на линии 45, масса каждого вагона 10 т, сопротивление трения равно 0,02 силы тяжести. Средняя скорость вагона 12км/ч и потери в сети 5%. Принять g = 10 м/с².

Дано: m = 10 т = 10·10³ кг; k = 45 вагонов; F = 0,02GV = 12 км/ч = 3,3 м/с,

η = 0,95.

Определить: P - ?

Решение:

Вес вагонов G = mg = 10· 10³ · 10 = 100 · 10³ Н = 100 кН.

Определяем полное сопротивление от трения:

F_тр = F · k = 0,02 · 100 · 45 = 90 кН.

Определяем полезную (эффективную) мощность турбогенераторов:

P_п = F_тр · v = 90 · 3,3 = 297 кВт.

Определяем полную (индикаторную) мощность турбогенераторов:

P = = = 312 кВт.

Ответ: P = 312 кВт.

• Определить работу, которую нужно произвести для того, чтобы сжать пружину на х = 10 см, если для сжатия ее на х₀ = 1 см необходима сила

F₀ = 100 Н.

Дано: x = 10 см; x₀ = 1 см; F₀ = 100 Н.

Определить: W - ?

Решение:

Работу, совершаемую при сжатии пружины, можно найти, построив график зависимости силы F, действующей на пружину, от величины ее деформации х, т.е. от величины смещения конца пружины из положения равновесия. По закону Гука эта сила равна F = cх, где c – коэффициент упругости пружины, равный в данном случае c = ==10⁴.

Работа сжатия пружины будет численно равна площади треугольника ОАВ:

W = = = == 50 Дж.

Ответ: W = 50 Дж.

54

• Поезд массой 60 т идет со скоростью 72 км/ч. На протяжении 1 км путь идет в гору, уклон которой равен 1/500, в следствие чего скорость поезда уменьшается до 60 км/ч. Определить силу тяги локомотива, если коэффициент сопротивления движению f = 0,01.

Дано: m = 60 т = 60 · 10³ кг; v₀ = 72 км/ч = 20 м/с; v = 60 км/ч = 16,7 м/с;

f = 0,01; S =1км = 1000 м.

Определить:F - ?

Решение:

В виду малости угла αможно принять sin α = tg α = 0,002; cоs α = 1.

Принимаем поезд за материальную точку. Покажем все силы, действующие на нее. Силу тяжести G раскладываем на составляющие:

G₁ = Gsinα = mg · sinα = 60·10·0,002 = 1,2кН;

G₂ = Gcоsα = mg · cоsα = 60·10·1 = 600 кН.

Определяем ускорение поезда из формул:

S = v₀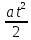t + иt= , отсюда

а = 0,061 м/с² – движение равнозамедленное.

Для определения силы тяги применим четвертый закон динамики(закон независимости действия сил). Спроектируем все действующие силы на оси Х иУ: 1. ΣХ = mа_х; F - G₁- F_тр = m (-а)

2. ΣУ = mа_у; N - G₂= 0.

Откуда N = G₂ - сила реакции;

F_тр = N_f – сила сопротивления (трения);

F – сила тяги локомотива.

Получим

F = m (-а) + G₁+F_тр = m (-а) + G₁ + G₂ = 60 · (-0,061) + 1,2 + 600 · 0,01 = 3,54 кН.

Ответ: F = 3,54 кН.

55

При решении задач по разделу «Сопротивление материалов» следует иметь в виду следующее. Стандартом СЭВ 1052-78 единицей давления, механического напряжения и модуля продольной упругости установлен 1 Н/м². Эта единица получила наименование паскаль(Па). Но паскаль – единица очень малая и для практических расчетов неудобна. Поэтому целесообразно использовать кратную ей единицу – мегапаскаль (МПа), причем 1 МПа = 10⁶ Па = 1 Н/мм²:

1 МПа = 10⁶ Па = = 1 Н/мм ².

Для построения эпюр надо применять метод сечений. Чтобы хорошо запомнить 4 операции, которые этот метод содержит, рекомендуется поставить слово «РОЗА» в винительном падеже, т.е. написать РОЗУ, тогда каждая буква этого слова будет означать содержание определенной операции метода сечений:

Р – разрезаем в произвольном месте нагруженный брус на две части,

О - отбрасываем одну какую – нибудь часть бруса и рассматриваем другую оставшуюся часть вместе с нагрузками, действующими на нее,

З – заменяем действие отброшенной части бруса на оставшуюся внутренними силами упругости, изображая в сечении не сами эти силы, а их статические эквиваленты или, другими словами, внутренние силовые факторы, к которым, по правилам статики приводятся внутренние силы упругости,

У – уравновешиваем оставшуюся часть бруса с действующими на него нагрузками статическими эквивалентами внутренних сил упругости, и, решая уравнения равновесия, находим их.

Обратите внимание на то, что метод сечений дает возможность найти лишь статические эквиваленты внутренних сил упругости, но вместе с тем не определяет ни величины этих сил в отдельных точках сечения, ни закон распределения их в сечении бруса.

Приступая к изучению сопротивления материалов, при решении рекомендованных задач на построение эпюр, необходимо применять все четыре операции метода сечений. В дальнейшем же, после приобретения навыков, можно, как это сделано в настоящем пособии, ограничиться только операцией Р, представив себе операции О, З, У лишь мысленно.

56