
Gidravlika_i_ghidromiekhanizatsiia_s.kh_._protsiessov__Praktikum
.pdf
Обозначение
z
p/γ
HП = z + гp
= αυ2
H υ 2g
H = z + γp + α2gυ
h
Таблица 3.6 — Основные составляющие уравнения Бернулли
|
Физический смысл |
Название, принятое в |
|
Геометрический смысл |
|
|||
|
гидравлике |
|
|
|||||
|
|
|
|
|
|
|
||
Удельная |
|
Положения |
Геометрический |
|
Геометрическая |
|
|
|
|
|
|
|
|
||||
жидковесаединицунаприходящаяся( |
|
|
|
|
|
|
|
|
|
Давления |
Пьезометрический |
|
Пьезометрическая |
|
|
||
|
|
|
|
Напор |
|
Высота |
отрезокВертикальный |
|
|
Потенциальная |
Потенциальный |
Потенциальная |
|||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Кинетическая |
Скоростной |
|
Скоростная |
|
|
|
|
|
(динамический) |
|
(динамическая) |
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Полная |
Полный |
|
Полная |
|
|
|
|
|
механическая |
гидродинамический |
|
гидродинамическая |
|
|
|
- |
|
|
|
|
|
|
|
|
Потери удельной ме- |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
ханической энергии, |
|
|
|
|
|
|
||
равные удельной ра- |
Потери напора на данном |
— |
|
|
||||
боте сил сопротивле- |
участке потока |
|
|
|
||||
|
|
|
|
|||||
ния на данном участ- |
|
|
|
|
|
|
||
ке потока |
|
|
|
|
|
|
||
Графическое изображение
Между плоскостью сравнения и центром тяжести сечения
Между центром тяжести сечения и пьезометрической линией (уровнем жидкости в пьезометре)
Между плоскостью сравнения и пьезометрической линией (уровнем жидкости в пьезометре)
Между пьезометрической и напорной линиями (проведенный вверх от уровня жидкости в пьезометре)
Между плоскостьюсравнения инапорнойлинией(верхним концомотрезка, представляющегосуммупотенциальногои скоростногонапора)
Равный разности полных напоров в соответствующих сечениях
в) геометрический уклон (уклон геометрической оси потока)
i |
= − |
∂z |
=sinϑ; |
i |
= |
z1 − z2 |
= |
∆z |
, |
(3.12) |
|
∂L |
|
l |
|||||||||
г |
|
|
гср |
|
L |
− L |
|
|
|
||
|
|
|
|
|
|
2 |
1 |
|
1−2 |
|
|
где ϑ — угол оси потока к горизонту;
l — расстояние вдоль оси потока между соответствующими сечениями. Взаимный переход потенциальной и кинетической энергии, который
описывается уравнением Бернулли, проявляется в потоке, имеющем разные площади поперечных сечений.
Наиболее удобной установкой, позволяющей изучить распределение видов энергии в потоке жидкости, является расходомер Вентури (рисунок 3.4), относящийся к типу дросселирующих расходомеров.
Вданном приборе границы потока изменяются плавно (угол конусности меньше 10º), поэтому уравнение Бернулли может быть применено к любым поперечным сечениям расходомера. Кроме того, этот прибор одновременно может быть использован по прямому назначению, то есть для измерения расхода.
Всемипоперечных сечениях прибора подключены пьезометры, которые объединены на общем щите и снабжены шкалой, имеющей общее начало отсчета – нулевую линию, то есть плоскость сравнения. Отсчет по такой шкале, соответствующей уровню жидкости в пьезометре, дает непосредственно потенциальный напор Нп = z + р/γ, (таблица 3.6 и рисунок 3.4).
Пьезометры, подключенные к начальному большому сечению (сечение 1) и к наиболее узкому сечению (сечение 4) используются также для измерения расхода. Эти пьезометры снабжены дополнительными стеклянными трубками, отсчеты по которым обозначены соответственно 1 и 2 . Для
удобства измерений дополнительные трубки установлены на краю щита отдельно от других пьезометров.
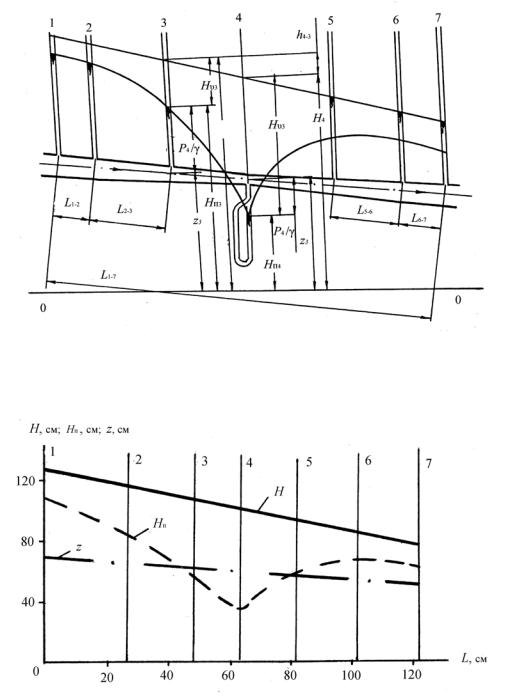
Рисунок 3.4 — Схема установки
Рисунок 3.5 — Графическое изображение уравнения Бернулли:
Н — напорная линия; Нп — пьезометрическая линия; z — геодезическая линия
Порядок выполнения работы
1. Ознакомиться с лабораторной установкой (для иллюстрации уравнения Бернулли используется расходомер Вентури):
а) записать площади S используемых вработе поперечных сечений;
б) измерить и записать расстояние L каждого сечения от начального (сечение 1);
63

в) измерить геометрический напор z для начального и конечного сечений (при измерении учесть, что плоскость сравнения проходит через нулевую линию шкалы пьезометров);
г) изучить порядок снятия отсчетов по пьезометрам и записать в таблицу 3.7
и3.9 соответствующие их шкале единицы измерения.
2.Запустить установку, вывести ее на рабочий режим и, убедившись, что он установился (уровень воды в напорном баке и пьезометрах не меняется), записать в таблицы 3.7 и 3.9 отсчеты по пьезометрам:
а) показывающим удельную потенциальною энергию (потенциальный напор Нп = z + p/γ) в сечениях 1–7;
б) измеряющим расход воды — 1 , 2 .
3.Определить и записать в таблицы 3.7, 3.8, 3.9:
а) разность показаний пьезометров расходомера ∆Нп б) расход воды Q (по тарировочному графику);
в) средние по сечению скорости v потока из уравнения неразрывности
Q = υS;
г) скоростные напоры Hυ = α υ2/2g, коэффициент кинетической энергии α взять с учетом режима движения жидкости;
д) полные напоры:
H = HП + Hх = z + p г + бх2 2 g ;
е) потери напора h, т. е. разность полных напоров ∆Н для участков 1–4 и 4–7 по уравнению Бернулли (3.9, а).
4. Построить на бумаге, имеющей координатную сетку, в одинаковом масштабе напорную Н = f1(L), пьезометрическую Нп = f2(L) и геодезическую z = f3(L) линии. Геодезическая линия строится по двум известным точкам (см. п. 1, в), поскольку ось потока на данной лабораторной установке представляет собой прямую линию (рисунок 3.5).
5. Определить и записать в таблицы 3.7, 3.8 и 3.9:
а) значение z для всех остальных сечений — с помощью геодезической линии; б) пьезометрический напор р/γ из формулы Нп = z+ р/γ;
64
в) длину участков 1–4 и 4–7, а также разность геометрических и потенциальных напоров ∆Hп для этих участков согласно формулам (3.11) и (3.12);
г) геометрический, пьезометрический и гидравлический уклоны для участков
1–4 и 4–7, используя формулы (3.12), (3.11), (3.10).
6. На графике для двух сечений (одно из них взять, где скоростной напор больший), показать все составляющие уравнения Бернулли, т. е. z, p/γ,
Нп, Нυ, H и h.
Таблица 3.7 — Напоры
Сечения |
|
S |
|
L |
|
z |
|
Нп |
υ |
|
Hυ |
H |
|
|
p/γ |
||||||
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.8 — Уклоны |
|
|
|
|
|
Таблица 3.9 — Расход |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Участок |
l |
|
∆z |
|
iг ср |
∆Нп |
iп.ср |
h |
|
iср |
|
|
1 |
|
2 |
∆Нп |
Q |
||||
1–4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4–7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3 Лабораторное занятие «Определение коэффициентов, характеризующих гидравлическое трение»»
Основные сведения
При движении жидкости возникают силы гидравлического сопротивления (трения), тормозящие движение. Различают вязкостные и инерционные сопротивления.
Вязкостные сопротивления возникают вследствие наличия у жидкости свойства сопротивляться при движении касательным усилиям, т. е. силам вязкости. Они проявляют свое действие главным образом в ламинарном потоке.
65

При турбулентном режиме движения, кроме вязкостных, возникают инерционные сопротивления, вызываемые образованием вихрей и перемешиванием масс жидкости, с увеличением числа Рейнольдса влияние инерционных сопротивлений возрастает и при развитом турбулентном режиме движения они становятся преобладающими.
На преодоление сил сопротивления затрачивается часть механической энергии жидкости (необратимо превращается в тепловую энергию). Теряемая при этом удельная механическая энергия называется потерей напора.
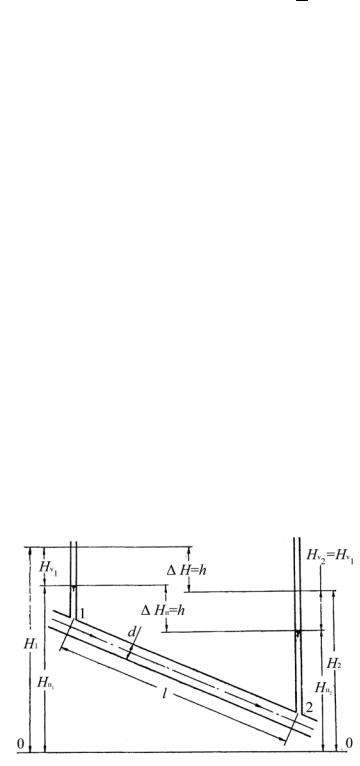
Потери напора на участке равномерного потока называются потерями напора по длине h. Опытное определение этих потерь производится на установке, схематично показанной на рисунке 3.6.
Из уравнения Бернулли следует
h = Н1 – Н2, (3.13)
где Н — полный напор в соответствующем сечении.
В равномерном потоке скоростные напоры Нυ во всех сечениях одинаковы, поэтому
h = Нп1 – Нп2 , |
(3.14) |
|||||
где Нп — потенциальный напор в соответствующем сечении. |
|
|||||
Важнейшей формулой дли вычисления потерь напора по длине являет- |
||||||
ся формула Дарси–Вейсбаха: |
|
|
|
|
|
|
h = л |
l |
|
х2 |
, |
(3.15) |
|
d 2g |
||||||
|
|
|
||||
где λ — коэффициент гидравлического трения; l — длина участка;
d — диаметр трубы;
υ — средняя скорость потока;
х2 — скоростной напор.
2g
В формуле (3.15) коэффициент кинетической энергии α входит в величину коэффициента гидравлического трения λ.
66
Коэффициент λ зависит в общем случае от режима движения жидкости
(числа Рейнольдса), относительной шероховатости∆, а также от формы выступов шероховатости. При расчетах величина λ определяется по графикам или соответствующим им таблицам и формулам.
Для труб круглого сечения относительная шероховатость:
|
= |
∆ |
, |
(3.16) |
∆ |
||||
|
|
d |
|
|
где ∆ — характерная высота выступов шероховатости (абсолютная шероховатость).
Вместо относительной шероховатости часто применяется обратная ей величина — относительная гладкость d/∆.
Дли потоков некруглого сечения в формулах (3.15 и 3.16) и в формуле
критерия Рейнольдса: |
|
|
|
|
Re = |
хd |
, |
(3.17) |
|
н |
||||
|
|
|
вместо значения диаметра d применяется величина 4R, где R — гидравлический радиус.
Рисунок 3.6 — Схема лабораторной установки для исследования потерь напора по длине
У большинства технических труб выступы шероховатости неодинаковы по высоте и по форме, размещены неравномерно, такая шероховатость называется разнозернистой, неоднородной, естественной. Для деревянных и
67

стеклянных труб характерна плавная, волнообразная форма выступов — волнистая шероховатость.
В целях обеспечения возможности инженерных расчетов труб, выпускаемых промышленностью (с естественной шероховатостью), были проведены исследования потерь напора по длине Кольбруком в 1938 году и Г.А. Муриным в 1948 году (рисунок 3.7). При развитом турбулентном движении коэффициенты λ совпадали. Абсолютная шероховатость, найденная из рас-
смотренного условия по формуле∆ = ∆d, называется эквивалентной шероховатостью. Она обычно приводится в справочниках (приложение 7).
Поскольку результаты исследований Кольбрука и Мурина практически совпадают, то достаточно рассмотреть график Мурина (приложение 8).
I. Зона ламинарного режима движения, (на графике Г.А. Мурина не показана); 0 < Rе < 2 300. Сопротивление движению определяется в основном силами вязкости. Коэффициент λ не зависит от шероховатости стенок и определяется по формуле Пуазейля:
λ = 64 / Re. (3.18) II. Зона переходного режима движения (на графике Г.А. Мурина не по-
казана); 2 300 < Rе < 4 000.
Выступы шероховатости покрыты ламинарным слоем. Сопротивление движению определяется в основном силами вязкости.
В данной зоне при одном и том же числе Rе в условиях эксплуатации технических труб режим движения жидкости переходит от ламинарного к турбулентному и обратно без видимых изменений условий эксплуатации. Зависимость коэффициента λ от числа Rе и шероховатости стенок становится неопределенной; расход, скорость и другие параметры потока меняются во времени. Поэтому поток при таком режиме движения является неустановившимся и мало пригодным для использования в технике, особенно в системах управления и автоматики.
Для установившегося турбулентного режима движения существуют еще три зоны сопротивления.
68
III. Зона гладкостенного сопротивления (гидравлически гладких труб) 4 000 < Rе < 10/ ∆.
Режим движения в середине потока турбулентный, но выступы шероховатости еще покрыты ламинарным слоем. Сопротивление движению определяется в основном силами вязкости у стенок и инерционными сопротивлениями в ядре потока. Коэффициент λ зависит только от величины критерия Rе. Потери напора пропорциональны υ1,75.
IV. Зона неразвитого турбулентного режима движения, или доквадратичного сопротивления (в технических трубах при неравномерной шероховатости потери напора пропорциональны υm, где 1,75 < m < 2, 10 / ∆ < Rе < 500 / ∆.
Толщина ламинарного слоя становится меньше выступов шероховатости, поэтому за ними образуются местные вихри. Это существенно увеличивает роль инерционных сопротивлений. Коэффициент λ в этой зоне зависит не только от числа Rе, но и от шероховатости.
V. Зона развитого турбулентного режима движения, или квадратичного сопротивления (потери напора пропорциональны υ2) Rе > 500 / ∆.
Ламинарный пристенный слой практически исчезает, вихри заполняют все впадины между выступами. Сопротивление движению определяется в основном инерционнымисилами. Коэффициентλзависиттолькоотшероховатости.
Для вычисления коэффициента λ предложен целый ряд формул, многие из которых имеют сложную структуру. Их применимость ограничена соответствующим диапазоном чисел Rе.
Например, для режимов, имеющих место в трубопроводах систем водоснабжения, СНиП 2.04.02.84 рекомендуется формула, которая для неновых стальных и чугунных труб без внутреннего защитного покрытия или с битумным защитным покрытием может быть приведена к виду
1 |
+ с/ х м |
(3.19) |
|
л = А |
|
, |
|
|
d |
|
|
где υ — средняя скорость движения воды, м/с;
69
d — диаметр трубы, м;
А, с, м — величины, определяемые в зависимости от скорости υ из таблицы 3.10. В этой таблице величина с дана для воды при темпера-
туре 10 °С. (ν = 1,3 × 10-6 м2/с).
Таблица 3.10
υ, м/с |
А |
с |
м |
< 1,2 |
0,017 9 |
0,867 |
0,3 |
> 1,2 |
0,021 |
0 |
0,3 |
Порядок выполнения работы
1.Ознакомиться с лабораторной установкой: а) определить и записать сведения об установке;
б) показать на схеме принятую на данной установке для рабочего участка трубопровода плоскость сравнения, его длину l, направление движения жидкости;
в) изучить порядок снятия отсчетов и место их записи в таблице.
2.Запустить установку, вывести ее на рабочий режим и, убедившись, что он установился (показания пьезометров не меняются, уровень воды в напорном баке поддерживается постоянным), измерить и записать в таблицу 3.11:
а) показания пьезометров в начальном и конечном сечениях (потенциальный напор Нп = z+ p/γ);
б) показания пьезометров 1 и 2 расходомера;
в) температуру воды t, °С.
3. Определить и записать в таблицу 3.11: а) расход водыQ (по тарировочному графику);
б) потери напора на исследуемом участке по формуле (3.14);
в) среднюю скорость υ с помощью уравнения неразрывности Q = υS; г) скоростной напор υ2/2g;
д) опытную величину коэффициента гидравлического трения λоп с помощью формулы Дарси–Вейсбаха (3.15);
70
