Продолжение 30

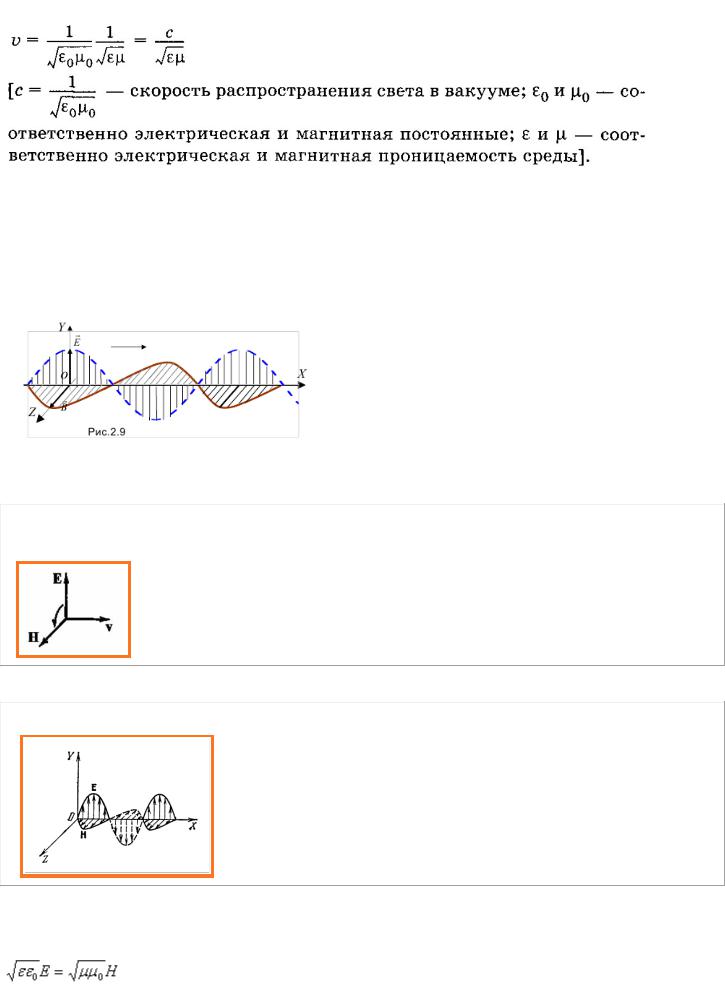
Фазовая скорость распространения электромагнитных волн в среде

Рассмотрим плоскую электромагнитную волну, распространяющуюся вдоль оси х, пер-

пендикулярной к волновым поверхностям. В этом случае, очевидно, поля и не зависят от координат y и z. Соответствующие уравнения Максвелла, записанные для этого случая, приводят к следующим скалярным волновым уравнениям:

, .

Свойстваэлектромагнитныхволн

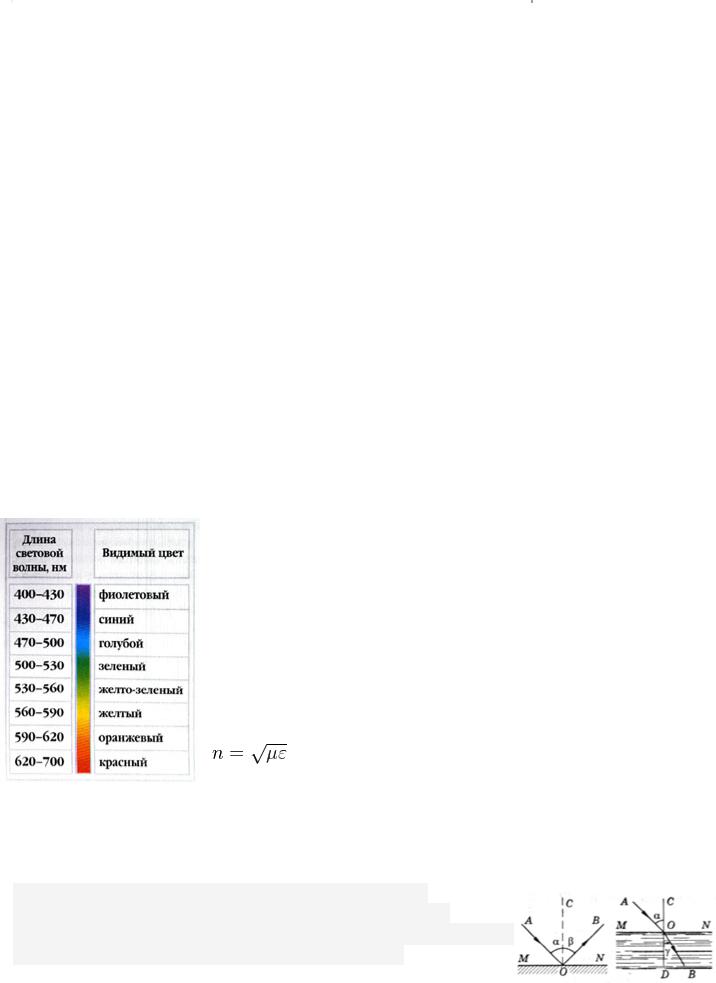
Электромагнитные волны - поперечные, то есть вектора E и H

колеблются по-

перек

поперёк направлению распространения волны.

Векторы Е и H взаимно перпендикулярны, так, что вектора v, E, H

образуют правую тройку

образуют правую тройку векторов.

Векторы Е и Н колеблются в одной фазе. Модули векторов Е и Н связаны соотношением:

31. Объемная плотность энергии электромагнитной волны. Поток энергии. Плотность потока энергии (вектор Умова-Пойнтинга). Интенсивность электромагнитной волны. Импульс электромагнитной волны. Давление света.

Плотностью потока энергии — средняя по времени энергия, которую электромагнитная или звуковая волна переносит в единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны

Через площадку S за время будет перенесена энергия заключенная в цилиндре с основанием S и высотой . Если размеры цилиндра достаточно малы (за счет малости S и ) для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, то можно найти как произведение плотности энергии w на объем цилиндра, S и и тогда получается, что энергия равна:

Подставим данную энергию в первоначальное уравнение и у нас получится:

В Формуле мы использовали :

— Интенсивность электромагнитной волны (плотностью потока энергии)

— Энергия волны

— Площадь поверхности

— Время

— Плотность энергии

— Скорость волны

Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:

Подставляя сюда выражения для wэ, wм и υ, можно получить:

Продолжение 31

Поток энергии в электромагнитной волне можно задавать с помощью вектора направление которого совпадает с направлением распространения волны, а модуль ра-

вен EB / μμ0. Этот вектор называют вектором Пойнтинга.

В синусоидальной (гармонической) волне в вакууме среднее значение Iср плотности потока электромагнитной энергии равно

где E0 – амплитуда колебаний напряженности электрического поля. В электромагнитном поле полный импульс частицы равен:

где — векторный потенциал электромагнитного поля.

Давлением света называется давление, которое производят электромагнитные световые волны, падающие на поверхность какого-либо тела. Давление р,оказываемое волной на поверхность металла, можно рассчитать как отношение равнодействующей сил Лоренца, действующих на свободные электроны в поверхностном слое металла, к площади поверхности металла:

p=∑nn=1F→iLS.

32. Шкала электромагнитных волн, световые волны. Показатель преломления среды и его связь с электромагнитными характеристиками среды. Изменение длины световой волны при переходе через границу двух сред. Принцип Гюйгенса и законы отражения и преломления света.

Показа́тель преломле́ния вещества — величина, равная отношению фазовых скоростей света (электромагнитных волн) в вакууме и в

данной среде .

Показатель преломления зависит от свойств вещества и длины волны излучения, для некоторых веществ показатель преломления достаточно сильно меняется при изменении частоты электромагнитных волн от низких частот до оптических и далее, а также может ещё более резко меняться в определённых областях частотной шкалы. Показатель преломления можно выразить как корень из произведения магнитной и диэлектрических проницаемостей среды

(надо при этом учитывать, что значения магнитной проницаемости и диэлектрической проницаемости для интересующего диа-

пазона частот — например, оптического, могут очень сильно отличаться от статических значений этих величин).

Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.

Закон отражения. Угол падения равен углу отражения Законы преломления. Луч падающий AO и преломленный

OB лежат в одной плоскости с перпендикуляром CD, проведенным в точке падения луча к плоскости раздела двух сред.

33. Явление интерференции света. Понятие когерентности волн. Условия наблюдения максимумов и минимумов при интерференции двух волн. Оптическая длина пути; оптическая разность хода двух световых волн. Связь между разностью фаз складываемых волн и их оптической разностью хода. Применение явления интерференции света.

Явление интерференции заключается в том что при наложении двух или более световых волн происходит устойчивое перераспределение светового потока в пространстве, в результате чего в одних местах возникают минимумы а в других максимумы интенсивности. Явление интерференции может наблюдаться только для когерентных волн.

Волны когерентны если: они имеют одинаковые частоты колебаний, раз-

Оптическая длина пути называют геометрическую длину пути, пройденную лучем в какой-либо среде умноженную на абсолютный показатель преломления этой среды.

Оптической разности хода двух световых волн называют величину равную разности оптических длин путей пройденных лучами.

Связь разности фаз от оптической разности хода световых волн:

ственные закономерности зависят от длины волны l0. Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн. Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий.

34. Способы получения интерференционной картины (щели Юнга, бизеркала и бипризма Френеля). Общая схема получения интерференционной картины. Ширина интерференционных полос. Расчет интерференционной картины от двух когерентных источников.

Пусть S — точечный источник света, расположенный перед экраном с двумя параллельными прорезя-

ми и , а — расстояние между прорезями, и D — расстояние между экраном с прорезями и проекционным экраном.

Точка М на экране имеет для начала одну координату x — расстояние между М иортогональной проекцией S на экране.

Существование интерференций зависит от разницы оптической длины между первым и вторым путем.

Пусть М — точка экрана, на которую падают одновременно два луча из и . Для — разницы оптической длины путей, имеем следующее соотношение:

где:

• — оптическая длина пути от источника до точки М на экране.

• — оптическая длина пути от источника до той же точки на экране.

Если a<<D и x<<D, то разница оптической длины пути в среде, с показателем преломления n, принимает упрощенное выражение:

В воздухе (при обычных условиях) . Выражение принимает вид:

Опыт Юнга

Зеркала Френеля.

Френель предложил в качестве двух когерентных источников воспользоваться двумя изображениями одного и того же действительного источника света в двух плоских зеркалах. Схема опыта Френеля представлена на рисунке, где A1O и А2O − два плоских зеркала, расположенных под углом φ; S − источник света, находящийся на расстоянии r от места соприкосновения зеркал в точке О.

Для построения изображений источника S в обоих зеркалах воспользуемся тем, что мнимое изображение, даваемое плоским зеркалом, лежит за зеркалом на таком же расстоянии, на каком объект лежит перед зеркалом. Проведем из точки О окружность с радиусом r = OS и опустим из точки S перпендикуляр на продолжение прямой ОА1; точка пересечения продолжения этого перпендикуляра с окружно-

стью В1 даст изображение источника S в первом зеркале ОА1. Так же построим изображение В2 даваемое во втором зеркале ОA2.

С другой стороны, изображение B2 лежит в той точке, куда переместилось бы изображениеВ1 при повороте первого зеркала ОА1 на угол φ.

Продолжение (34)

Поэтому <B1OB2 = 2φ, и линейное расстояние d между В1 и В2 приближенно равно 2φr:

d = 2φr. (1)

Свет от обоих изображений В1 и В2 падает на экран DD/, отстоящий от зеркал на расстоянии Lo. Заслонка Е мешает попадать на экран DD/ прямому свету от источника S. Так как оба изображе-

ния B1 и В2 воспроизводят колебания одного и того же действительного источника, то они когерентны, и на экране DD/ наблюдаются интерференционные полосы. Расстояние между полосами Δl равно

Δl = λL/d,

где L − расстояние от источников до места наблюдения полос. Подставляя сюда вместо d его значение по (1) и замечая, что приближенно

L = Lo + r,

получим

Δl = (Lo + r)λ/(2φr),

или отсюда

λ = 2φr•Δl/(Lo + r).

Так как в последней формуле все величины, стоящие в правой части, доступны измерению, то из нее видно, что опыт с зеркалами Френеля позволяет измерить длину световых волн λ.

Зеркала в опыте Френеля приходится располагать под весьма малым углом φ друг к другу, так как иначе полосы получаются слишком узкими. Источник света берется в виде узкой щели, параллельной ребру О, образованному зеркалами. При этом интерференционные максимумы имеют вид прямых параллельных полос. При наблюдении в белом свете центральная полоса получается белая (k = 0, усиливаются лучи всех длин волн λ), остальные − окрашенные.

Бипризма Френеля.

Этот опыт представляет собою простой вариант с бизеркалами Френеля.

Свет от источника S преломляется в двух призмах с малыми преломляющими углами A и A/(рисунок), сложенных основаниями.

Призмы отклоняют лучи в противоположных направлениях и, таким образом, возникают два мнимых когерентных источника света S/ и S//. Лучи от этих источников, перекрываясь в области D, дают интерференционные полосы.

Общая схема получения интерференционной картины

Основной принцип любой интерференционной схемы по получению когерентных световых волн от обычных источников состоит в следующем волну излучаемую Одним источником света разделяют тем или иным способом на две части и затем

Накладывают их друг на друга подходящим способом. Образовавшиеся после разделения волны во всех схемах можно представить как бы исходящими из двух точечных источников S1 и S2 действительных или мнимых. Если разность хода Этих волн от источника до точки наблюдения не превышает некоторой характерной

Длины то случайные изменения амплитуды и фазы световых колебаний в двух волнах Происходят согласованно когерентно и можно будет наблюдать интерференционную картину.

Продолжение (34)

Ширина интерференционных полос. Обычно экран для наблюдения интерференционной картины располагают так, чтобы оба луча и нормаль к экрану находились в одной плоскости. В этом случае ширина интерференционных полос полностью определяется углами падения световых волн на экран и длиной световой волны и не зависит от оптической схемы формирования интерферирующих волн.

Пусть две плоские световые волны падают на экран под углами и (рис. 19), точки и - середины двух соседних светлых полос на экране, - поверхность равной фазы первой волны, - поверхность равной фазы второй волны. Поверхность имеет ту же фазу, что и поверхность , так как в точке

фазы двух волн одинаковые (светлая полоса). Поэтому можно считать, что это одна и та же поверхность равной фазы волны, идущей от одного точечного источника разными путями. Следовательно, оптическую раз-

ность хода, например для точки экрана , можно отсчитывать от пары точек и как бы общей поверхности равной фазы.

Из рис. 19 видно, что поверхность равной фазы первой волны еще не дошла до точки на отрезок , а поверхность второй волны уже зашла за точку на отрезок . Тогда оптическая разность хода для

точки равна

.

Точки и - середины соседних светлых полос, тогда оптическая разность хода равна длине волны

, так как при переходе по экрану на одну полосу разность хода меняется на . Выражая из этого равенства ширину полосы , и обозначая ее через , получаем

,

где знак '+' соответствует положительным углам падения 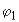и отсчитанным в разные стороны от нормали к экрану, как на рис. 19.

Расчет интерференционной картины для двух источников можно провести используя две узкие па-

раллельные щели, расположенные достаточно близко друг к другу.

Щели S1 и S2 находятся на расстоянии d друг от друга и являются когерентными источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей. Интенсивность в Продолжение (34)

любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода (разностью оптических длин проходимых волнами путей). Из рисунка имеем: откуда или . Из условия l>>d следует, что поэтому . Подставив найденное значение в условия интерференционного максимума и минимума: и , получим, что максимумы интенсивности будут наблюдаться при , а минимумы — при . Расстояние между двумя соседними максимумами (или минимумами) называемое шириной интерференционной полосы равно: . не зависит от порядка интерференции (величины m) и является постоянной для . обратно пропорционально d, след. при большом расстоянии между источниками, например,

, отдельные полосы становятся неразличимыми. Из двух предпоследних формул следует так же, что интерференционная картина , создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m=0, проходит через точку О. Вверх и вниз от него, на равных расстояниях располагаются максимумы (минимумы) первого (m=1) и других порядков. Описанная картина справедлива только лишь при освещении монохроматическим светом. Если использовать белый свет, то интерференционные максимумы для каждой длины волны будут смещены друг относительно друга и иметь вид радужных полос. Только для m=0 максимумы всех длин волн совпадают, а в середине экрана будет наблюдаться белая полоса.

35. Интерференция в тонких пленках. Полосы равного наклона (при отражении света от плоскопараллельной пластинки). Выражения для оптической разности хода интерферирующих лучей при наблюдении полос равного наклона. Применение явления интерференции света.

Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта. Один из способов, использующих такой метод, – опыт Поля.

В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки (рис. 8.7).

В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.

Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S1 и S2 источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт

предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.

ПОЛОСЫ РАВНОГО НАКЛОНА - чередующиеся тёмные и светлые полосы (интерференционные полосы), возникающие при падении света на плоскопараллельную пластину в результате интерференции лучей, отражённых от верхней и нижней её поверхностей и выходящих параллельно друг другу. Монохроматиче-

ский свет с длиной волныот точечного источника S (рис.), находящегося в среде с показателем преломления п, падает на пластину толщиной h и с показателем

преломленияпри отражении луча SA от верхней и

нижней граней образуются параллельные лучи AD и СЕ. Оптическая разность хода между такими лучам, а соответствующая разность фаз

С учётом сдвига фаз на при отражении т. е. при постоянстве h и разность фаз определяется наклоном лучей относительно пластины: при равном наклоне p разность фаз постоянна. Чтобы лучи AD и СЕ интерферировали, необходимо их совмещение, что достигается для параллельных лучей в бесконечности. Наблюдаются они при аккомодации глаз на бесконечность или с помощью линзы, в фокусе к-рой помещают экран. Раз-

ность фазне связана с положением источника света: лучи, испущенные соседней точкой источника и

отражённые под тем же угломбудут иметь ту же разность фаз, а при проецировании на экран попадут в ту же точку. Поэтому при использовании протяжённого источника полосы оказываются столь же отчётливыми, как и с точечным источником.

Применение явления интерференции света.

Явление интерференции обусловлено волновой природой света; его количественные закономерности зависят от длины волны l0. Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн. Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий.

35. Интерференция в тонких пленках. Полосы равной толщины (при отражении от клиновидной пластинки, кольца Ньютона). Применение явления интерференции света.

Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта. Один из способов, использующих такой метод, – опыт Поля.

В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки (рис. 8.7).

В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.

Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S1 и S2 источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт

предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.

ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ - интерференц. по-

лосы, наблюдаемые при освещении тонких оптически прозрачных слоев (плёнок) переменной толщины пучком параллельных лучей и обрисовывающие линии равной оптической толщины. П. р. т. возникают, когда интерференц. картина локализована на самой плёнке. Разность хода между параллельными монохроматич. лучами, отражёнными от верхней и нижней поверхностей

плёнки (рис.), равна (n - показатель преломления плёнки, h - её толщина,- угол преломления). Учитывая изменение фазы напри отражении от одной из поверхностей плёнки, получим, что

максимумы интенсивности (светлые полосы) возникают при разности хода

m = 0,1, 2, ..., а минимумы (тёмные полосы) - при

- длина волны света, в к-ром происходит наблюдение). Условие параллельности лучей выполняется, если расстояние от источника света до плёнки значитель-

но больше -расстояния между точками пересечения интерферирующих лучей с поверхностью плёнки. При достаточно малом зрачке наблюдат. прибора это условие выполняется и для протяжённого источника.

Примером регулярных П. р. т., образующихся в воздушном зазоре между двумя сферич. поверхностями или сферой и плоскостью, являются Ньютона кольца .При освещении белым светом разл. толщинам h будут соответствовать разл. l, для к-рых слой обладает наиб. прозрачностью и наим. отражат. способностью. Это создаёт при малых h радужную окраску тонких плёнок (мыльных пузырей, масляных и бензиновых пятен).

Применение явления интерференции света.

Явление интерференции обусловлено волновой природой света; его количественные закономерности зависят от длины волны l0. Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн. Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий.

37. Дифракции света. Условие наблюдения дифракции света. Принцип Гюйгенса-Френеля. Метод

зон Френеля. Формулы для расчета радиуса и площади m-й зоны Френеля. Доказательство прямолинейного распространения света в однородной среде. Зонная пластинка.

Дифракцией называется отгибание волнами препятствий.

Условие наблюдения дифракции света. Если на пути световой волны находятся непрозрачные тела или экраны с отверстиями, то грубые

наблюдения показывают, что за этими телами образуется область тени. Эту область можно очертить геометрически, полагая, что свет распространяется прямолинейно, световые лучи есть прямые линии.

Принцип Гюйгенса-Френеля.

Согласно этому принципу, первоначально введённому голл. учёным X. Гюйгенсом каждый элемент поверхности, к-рой достигла в данный момент волна, явл. центром элем. волн, огибающая к-рых будет волн. поверхностью в следующий момент времени (рис. 1); обратные элем. волны (пунктирные линии) во внимание не принимаются. Этот принцип упрощает задачу определения влияния всего волн. процесса, совершающегося в нек-ром объёме, на к.-л. точку, сведя её к вычислению действия на данную точку про-

извольно выбранной волн. поверхности. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не объясняет явлений дифракции Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порож-

дающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Метод зон Френеля. Формулы для расчета радиуса и площади m-й зоны Френеля.

представляет собой в общем случае очень трудную задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическим или геометрическим суммированием.

Найдем в произвольной точке М амплитуду сферической световой волны, распространяющейся в однородной среде из точечного источника S.

Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Френель разбил волновую поверхность A на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на λ/2,

Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке разбиения фронта волны на зоны можно выполнить, проведя с центром в точке М сферы радиусами

Продолжение 37

Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на λ/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке

М:

где А1, А2, … Аm − амплитуды колебаний, возбуждаемых 1-й, 2-й, …, m-й зонами.

Для оценки амплитуд колебаний найдем площади зон Френеля. Пусть внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты hm (рис.).

Обозначив радиус этого сегмента через rm, найдем, что площадь m-й зоны Френеля:

здесь σm-1 − площадь сферического сегмента, выделяемого внешней границей m − 1-й зоны. Из рисунка следует, что

После элементарных преобразований, учитывая, что λ << a и λ << b, получим

Площадь сферического сегмента и площадь m-й зоны Френеля: где Δσm площадь m-й зоны Френеля, которая, как показывает последнее выражение, не зависит от m. При не слишком больших m площади зон Френеля одинаковы.

Таким образом, построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны.

Найдем радиусы зон Френеля

откуда

Закон прямолинейного распространения света. Как показывают наблюдения, в однородной среде свет распространяется прямолинейно. Другими словами, в однородной среде световые лучи представляют собой прямые линии.

Чтобы доказать это, проведем по линейке отрезок прямой линии на листе картона. Воткнем у концов отрезка и в его середине по булавке и посмотрим вдоль начерченной линии. Если линия прямая, то ближайшая к нам булавка будет заслонять остальные. Это означает, что световые лучи, идущие вдоль прямой от дальней булавки как от источника света, не попадают к нам в глаза, так как на их пути встречается непрозрачная преграда. Глядя вдоль начерченной линии, можно таким образом проверить ее прямолинейность.

Зонная пластинка — плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. Зонная пластинка «выключает» чётные либо нечётные зоны Френеля, чем исключает взаимную интерференцию (погашение) от соседних зон, что приводит к увеличению освещённости точки наблюдения. Таким образом, зонная пластинка действует как собирающая линза.

38. Метод зон Френеля. Формулы для расчета радиуса и площади m-й зоны Френеля. Дифракция Френеля на круглом отверстии. Дифракция Френеля на круглом диске.

Метод зон Френеля. Формулы для расчета радиуса и площади m-й зоны Френеля.

представляет собой в общем случае очень трудную задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическим или геометрическим суммированием.

Найдем в произвольной точке М амплитуду сферической световой волны, распространяющейся в однородной среде из точечного источника S.

Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Френель разбил волновую поверхность A на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на λ/2,

Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке разбиения фронта волны на зоны можно выполнить, проведя с центром в точке М сферы радиусами

Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на λ/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М:

Продолжение (38)

где А1, А2, … Аm − амплитуды колебаний, возбуждаемых 1-й, 2-й, …, m-й зонами.

Для оценки амплитуд колебаний найдем площади зон Френеля. Пусть внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты hm (рис.).

Обозначив радиус этого сегмента через rm, найдем, что площадь m-й зоны Френеля:

здесь σm-1 − площадь сферического сегмента, выделяемого внешней границей m − 1-й зоны. Из рисунка следует, что

После элементарных преобразований, учитывая, что λ << a и λ << b, получим

Площадь сферического сегмента и площадь m-й зоны Френеля: где Δσm площадь m-й зоны Френеля, которая, как показывает последнее выражение, не зависит от

Продолжение 38

m. При не слишком больших m площади зон Френеля одинаковы.

Таким образом, построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны.

Найдем радиусы зон Френеля

откуда

Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и

(177.6)),

где знак плюс соответствует нечетным m и минус — четным т.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А1, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых Продолжение (38)

колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины. Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то Аm<<A1 и результирующая амплитуда A=A1/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.

Продолжение 38

2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

или

так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

Продолжение (38)

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается уголт (см. рис. 258) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.

39. Дифракция Фраунгофера на одной щели. Условия наблюдения дифракционных максимумов и минимумов при дифракции света на одной щели. Влияние ширины щели на дифракционную картину.

Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис. 261, а). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении ,

(179.1)

где F — основание перпендикуляра, опущенного из точки М на луч ND.

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна /2, т. е. всего на ширине щели уместится : /2 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Из выражения (179.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла . От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то

(179.2)

и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля не-

четное, то

(179.3)

и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в направлении =0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке В0 наблюдается цен-

тральный дифракционный максимум.

Из условий (179.2) и (179.3) можно найти направления на точки экрана, в которых амплитуда (а следовательно, и интенсивность) равна нулю (sin min = m /a) или максимальна (sin max = (2m+1) /(2a)). Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр), приведено на рис. 261, б.

Продолжение (39)

Расчеты показывают, что интенсивности в центральном и последующих максимумах относятся как 1 : 0,047 : 0,017 : 0,0083 : .... т.е. основная часть световой энергии сосредоточена в центральном максимуме.

Из опыта и соответствующих расчетов следует, что сужение щели приводит к тому, что центральный максимум расплывается, а интенсивность уменьшается (это, естественно, относится и к другим максимумам). Наоборот, чем щель шире (а> ), тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При а>> в центре получается резкое изображение источника света, т. е. имеет место прямолинейное распространение света.

Продолжение 39

Положение дифракционных максимумов зависит от длины волны , поэтому рассмотренная выше дифракционная картина имеет место лишь для монохроматического света. При освещении щели белым светом центральный максимум наблюдается в виде белой полоски; он общий для всех длин волн (при =0 разность хода равна нулю для всех ). Боковые максимумы радужно окрашены, так как условие максимума при любых т различно для разных . Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (m=1), второго (т=2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.

Влияние ширины щели на вид интерференционной картинки.

С уменьшением ширины щели центральная полоса расширяется, так как первый минимум отодвигается от центра. При ширине щели, равной длине волны угол, соответствующий первому минимуму, становится равным 90°, освещенность экрана монотонно уменьшается от центра к краям. При

дальнейшем уменьшении ширины щелиосвещенность стремится стать равномерной по всему экрану.

Если увеличивать ширину щели, то максимум становится все более резким, а яркость изображения увеличивается, так как увеличивается энергия, прошедшая в щель. Если ширина щели много больше длины волны получаем резкий максимум (если источник – линейный получаем узкую полосу) . Это – случай геометрической оптики.

Влияние размеров источника света на вид интерференционной картинки.

Пусть наш источник света – не точечный , а имеет конечные размеры. Такой источник можно представить как совокупность некогерентных точечных источников, каждый из которых даёт свою интерференционную картину. Все эти картинки смещены друг относительно друга (рис. 5). Пусть угловой размер источника равен 2α. Ширина центрального интерференционного максимума равна 2λ/b. Вид дифракционной картинки зависит от соотношения этих двух углов (Рис.6).

Если λ/b<< α, (широкая щель или большой источник) то изображение геометрически подобно источнику, дифракция мала.

40. Дифракционная решетка. Вывод условия главных максимумов для одномерной дифракционной решетки; условия главных дифракционных минимумов для дифракционной решетки. Формула для нахождения наибольшего числа главных максимумов. Объяснение вида дифракционной картины при освещении решетки белым светом.

Дифракционная решетка - оптический прибор, представляющий собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками. Число штрихов у хороших дифракционных решеток доходит до нескольких тысяч на 1 мм.

Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис. 261, а). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении ,

(179.1)

где F — основание перпендикуляра, опущенного из точки М на луч ND. Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна/2, т. е. всего на ширине щели уместится : /2 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Из выражения (179.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла . От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если

число зон Френеля четное, то

(179.2)

и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то

(179.3)

и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля.

Продолжение 40

Формула для нахождения наибольшего числа главных максимумов.

Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности

d sinφ=±kλ, k=0,1,2,3,…,

где d — период (постоянная) решетки; k — номер главного максимума; φ — угол между нормалью к поверхности решетки и направлением дифрагированных волн.

Объяснение вида дифракционной картины при освещении решетки белым светом.

Если ширина прозрачной щели (или отражающих полос) а, а ширина непрозрачных промежутков (или рассеивающих свет полос) b, то величина d = а + b

называется периодом решетки.

Пусть на решетку падает плоская монохроматическая волна длиной А (рис. 106.). Вторичные волны за дифракционной решеткой распространяются по всем направлениям. Найдем условие, при котором вторичные волны усиливают друг друга.

Рассмотрим волны, идущие под углом (р. Разность хода между волнами от краев соседних щелей равна длине отрезка АС. В треугольнике АСВ катет | АС | = | АВ | sin ф = d sin ф. Максимум будет наблюдаться, если | АС | = kЛ, то есть

При выполнении этого условия усилят друг друга волны, идущие от всех других точек щелей. Для наблюдения дифракционной картины за решеткой помещают собирающую линзу, в фокусе которой располагается экран. Линза фокусирует лучи, идущие параллельно, в одной точке. В этой точке происходит сложение волн и их взаимное усиление. При освещении решетки монохроматическим светом в направлении ф = 0 наблюдается максимум нулевого порядка - центральный. Но обе стороны от него наблюдаются максимумы 1- го, 2-го и т. д. порядков. При освещении белым светом происходит его разложение в спектр: максимумы волн разной длины, кроме центрального, наблюдаются под разными углами.

41. Дифракция рентгеновских лучей на кристаллах. Формула Вульфа-Брэггов. Понятие о рентгеноструктурном анализе и рентгеновской спектроскопии

1)Дифракция рентгеновских лучей на кристалах- рассеяние рентгеновских лучей кристаллами, при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта. Дифрагированные пучки составляют часть всего рассеянного веществом рентгеновского из лучения. Явление Д. р. л., доказывающее их волновую природу, впервые было экспериментально обнаружено на кристаллах немецкими физиками М. Лауэ, В. Фридрихом и П. Книппингом в 1912.

2) Условие Брэгга — Вульфа- условие, определяющее положение интерференционных максимумов рентгеновских лучей, рассеянных кристаллом без изменения длины волны. Б.— В. у. установлено в 1913 независимо друг от друга английским учёным У. Л. Брэггом и русским учёным Г. В. Вульфом вскоре после открытия немецким учёным М. Лауэ и его сотрудниками дифракции рентгеновских лучей. Согласно теории Брэгга — Вульфа, максимумы возникают при отражении рентгеновских лучей от системы параллельных кристаллографических плоскостей, когда лучи, отражённые разными плоскостями этой системы, имеют разность хода, равную целому числу длин волн. Б. — В. у. можно записать в следующем виде:

2dsinJ = m,

где d — межплоскостное расстояние, J — угол скольжения, т. е. угол между отражающей плоскостью и падающим лучом, l — длина волны рентгеновского излучения и m — так называемый, порядок отражения, т. е. положительное целое число (см. рис.).

Б. — В. у. выполняется при рассеянии кристаллами не только рентгеновских лучей, но также g-лучей, при дифракции электронов, протонов и нейтронов.

Метод Д. р. л. на кристаллах дал возможность определять длину волны рентгеновских лучей, если известна структура кристаллической решётки, благодаря чему возникла рентгеновская спектроскопия, сыгравшая важную роль при установлении строения атома. Наблюдения Д. р. л. известной длины волны на кристалле неизвестной структуры позволяют установить характер этой структуры (расположение ионов, атомов и молекул, составляющих кристалл), что послужило основой рентгеновского структурного анализа.

3) Рентгеновская спектроскопия, получение рентгеновских спектров испускания и поглощения и их применение к исследованию электронной энергетической структуры атомов, молекул и твёрдых тел. Рентгеновские спектры испускания получают либо бомбардировкой исследуемого вещества, служащего мишенью в рентгеновской трубке, ускоренными электронами (первичные спектры), либо облучением вещества первичными лучами (флуоресцентные спектры)

Рентгеновские спектры поглощения образуются при пропускании узкого участка спектра тормозного излучения через тонкий слой исследуемого вещества.

Рентгеновский структурный анализ, методы исследования структуры вещества по распределению в пространстве и интенсивностям рассеянного на анализируемом объекте рентгеновского излучения. Р. с. а. наряду с нейтронографией и электронографией является дифракционным структурным методом; в его основе лежит взаимодействие рентгеновского излучения с электронами вещества, в результате которого возникает дифракция рентгеновских лучей.

Р. с. а. изучает металлы, сплавы, минералы, неорганические и органические соединения, полимеры, аморфные материалы, жидкости и газы, молекулы белков, нуклеиновых кислот и т.д. Наиболее успешно Р. с. а. применяют для установления атомной структуры кристаллических тел. Это обусловлено тем, что кристаллы обладают строгой периодичностью строения и представляют собой созданную самой природой дифракционную решётку для рентгеновских лучей.

42. Поляризация света. Естественный и поляризованный свет; основные виды поляризации света; плоскость поляризации. Способы получения линейно поляризованного света. Степень поляризации света. Поляризация света при отражении и преломлении света на границе раздела двух диэлектриков. Закон Брюстера.

1)Согласно электромагнитной теории света свет представляет собой поперечные электромагнитные волны. Электромагнитная волна описывается двумя взаимно перпендикулярными векторами напряженности полей: электрического E и магнитного H изменяющимися в одинаковой фазе и перпендикулярными к направлению распространения волны (вектору скорости v волны). 2)Обычные источники света являются совокупностью огромного числа быстро высвечивающихся элементарных излучателей(атомов, молекул), испускающих независимо друг от друга волны с различными направлениями светового вектора. При наложении друг на друга эти волны образуют результирующую волну, в которой колебания светового вектора, перпендикулярные направлению распространения волны, происходят в различных плоскостях и быстро (~10-8 с) и беспорядочно сменяют друг друга. Такой свет называют

естественным, или неполяризованным.

Если колебания светового вектора E упорядочены каким-либо образом, то такой свет называется поляризованным.

3) Различают следующие виды поляризации:

1.Плоско- (или линейно)поляризованный свет. Колебания век-тора E происходят в одной плоскости, проходящей через луч.

2.Свет, поляризованный по кругу (круговая поляризация). Плоскость колебаний вектора E вращается вокруг направления распро-странения света, модуль E остается постоянным.

3.Эллиптически поляризованный свет. Плоскость колебаний вектора E вращается вокруг направления распространения света (волны), и вектор E изменяется по модулю. Способы получения линейно-поляризованного света

4)Свет, в котором имеется преимущественное направление колебаний векто-

ра и незначительная амплитуда колебаний вектора 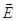в других направлени-

ях, называется частично поляризованным.

В плоско поляризованном свете плоскость, в которой колеблется вектор , называется плоскостью поляризации, плоскость, в которой колеблется век-

тор , называется плоскостью колебаний.

Вектор называют световым вектором потому, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества.

Продолжение 42

Степенью поляризации называется величина

где Imax и Imin – максимальная и минимальная компоненты интенсивности света, соответствующие двум взаимно перпендикулярным компонентам векто-

ра (то есть Ех и Еу – составляющие). Для плоско поляризованного света Еу = Е, Ех = 0, следовательно, Р = 1. Для естественного света Еу = Ех = Е и Р = 0. Для частично поляризованного света Еу = Е, Ех = (0...1)Еу, следовательно, 0 <Р < 1.

Если вектор в эллиптически поляризованном свете вращается при распространении света по часовой стрелке, то поляризация называется правой, против - левой. В эллиптически поляризованном свете колебания полностью упорядочены. К эллиптически поляризованному свету понятие степени поляризации не применимо, так что Р=1 всегда.

Способы получения линейно-поляризованного света

1.Наиболее просто поляризационный свет можно получить из естественного света при отражении световой волны от границы раздела двух диэлектриков.Если естественный свет падает на границу раздела двух диэлектриков (например, воздух-стекло), то часть его отражается, а часть преломляется и распространяется во второй среде.

Закон Брюстера:

При угле падения, равном углу Брюстера іБр: 1. отраженный от границы раздела двух диэлектриков луч будет полностью поляризован в плоскости, перпендикулярной плоскости падения; 2. степень поляризации преломленного луча достигает максимального значения меньшего единицы; 3. преломленный луч будет поляризован частично в плоскости падения; 4. угол между отраженным и преломленным лучами будет равен 90°; 4. тангенс угла Брюстера равен относительному показателю преломления

- закон Брюстера.

n12 - показатель преломления второй среды относительно первой. Угол падения (отражения) - угол между падающим (отраженным) лучом и нормалью к по-

верхности. Плоскость падения - плос-

кость, проходящая через падающий луч и нормаль к поверхности

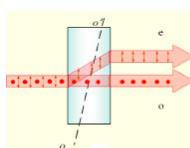
43. Двойное лучепреломление в анизотропных кристаллах. Обыкновенный и необыкновенный лучи, оптическая ось кристалла, главное сечение (главная плоскость) кристалла. Зависимость диэлектрической проницаемости анизотропных

кристаллов от напряженности электрического поля E . Образование обыкновенно-

го и необыкновенного лучей, их скорости и показатели преломления. Получение линейно поляризованного света с помощью анизотропных кристаллов (призма Николя, поляроид).

Поляризация при двойном лучепреломлении.

Явление двойного лучепреломления заключается в том, что при прохождении света через многие прозрачные кристаллы падающий световой луч внутри кристалла разделяется на два луча, которые, как правило, распространяются в различных направлениях, с разными скоростями и линейно-поляризованы во взаимно перпенди-кулярных направлениях. Это явление было обнаружено в конце XVII века при изучении кристаллов исландского шпата (CaCO3) (рис. 1.18). У некоторых кристаллов есть только одно направление (ОО′ — называются одноосными. К ним относятся исландский шпат, кварц, турмалин. В общем случае в двулучепреломляющих кристаллах имеется два направления, в которых не происходит двойного лучепреломления. Эти направления называются оптическими осями кристалла. Такие кристаллы называются двуосными. К ним относятся слюда, гипс. Любая плоскость, проходящая через оптическую ось, называется главным сечением, или главной плоскостью кристалла. Обычно пользуются главным сечением, проходящим через световой луч.

У одноосных кристаллов один из преломленных лучей подчиняется обычному закону преломления и называется обыкновенным (обозначается буквой «о»). Показатель преломления no обыкновенного луча не зависит от направления распространения его в кристалле. Для другого луча,

называемого необыкновенным (обозначают буквой«е»), отношение синусов угла падения и угла преломления не остается постоянным при изменении угла падения(луч не подчиняется закону преломления). Даже при нормальном падении света на кристалл этот луч отклоняется от первоначального направления. Для необыкновенного луча показатель преломления ne зависит от направления в кристалле. Оба луча, обыкновенный и необыкновенный, полностью поляризованы во взаимно перпендикулярных направлениях. Колебания электрического вектора E в обыкновенном луче перпендикулярны к плоскости главного сечения кристал-ла, а в необыкновенном луче вектор E колеблется в плоскости главного сечения. Названия «обыкновенный» и «необыкновенный» имеют смысл только внутри кристалла, по выходе из кристалла оба луча отличаются друг от друга только плоскостями поляризации. Явление двойного лучепреломления можно использовать для получения линейно поляризованного света из естественного, выделив один из двух лучей. На практике линейно-поляризованный свет получают с помощью специальных поляризационных устройств.

Поляризацию Д. характеризуют вектором поляризации P, который представляет собой дипольный момент единицы объёма Д. Дипольный момент нейтральной в целом системы зарядов есть вектор, равный произведению расстояния между центрами тяжести положительных и отрицательных зарядов на величину заряда одного знака. Направлен этот вектор от центра тяжести отрицательных к центру тяжести положительных зарядов. Вектор P зависит от напряжённости электрического поля Е. Поскольку сила, действующая на заряд, пропорциональна Е, то, естественно, что при малых полях величи-

на Рпропорциональна Е. Коэффициент пропорциональности c в соотношенииP =

cЕ называется диэлектрической восприимчивостью Д. Часто оказывается удобным вместо вектора P пользоваться вектором электрической индукции.

Продолжение 43

D = Е + 4pP.

Коэффициент пропорциональности e в соотношении D = eЕ называется диэлектрической проницаемостью. Ясно, что

e = 1 + 4pc.

В вакууме c = 0 и e = 1 (в системе единиц СГСЕ). Значение e (или c) является основной характеристикой Д.

В анизотропных Д. (например, в некубических кристаллах) направление вектора поляризации Pопределяется не только направлением поля Е, но также выделенными направлениями среды, например осями симметрии кристалла. Поэтому вектор P будет составлять различные углы с векторомЕ в зависимости от ориентации Е по отношению к осям симметрии. В результате вектор D будет определяться через вектор E с помощью не одной величины e, а несколькими величинами (в общем случае — шестью), образующи-

ми тензор диэлектрической проницаемости

Призма Николя. Рассмотрим в качестве примера призму Николя. Это устройство изобрел шотландский физик Николь в 1828 г. Изготавливается оно из кристалла исландского шпата. Показатели преломления для него равны: no = 1,6585 и ne = 1,4863. Из кристалла, разрезанного специальным образом, изготавливают две призмы. Эти призмы склеивают канадским бальзамом. В результате получается следующая конструкция призмы Николя

Естественный световой луч в кристалле разделяется на два луча — обыкновенный АО и необыкновенный АЕ. Благодаря конструкции призмы Николя необыкновенный луч проходит через границу двух склеенных частей кристалла, а обыкновенный луч испытывает полное внутреннее отражение и выводится из кристалла с помощью призмы П. Выходящий из призмы Николя луч АЕ полностью линейно-поляризован.

Поляроиды. Для получения линейно-поляризованного света большое распространение получили поляризующие пленки - поляроиды. Поляроид —это пленка прозрачного вещества, на которую тон-ким слоем нанесены определенным образом ориентированные микроскопические кристаллики турмалина или герапатита(сернокислого йод-хинина).

Эти кристаллы являются двулучепреломляющими. Кроме того в этих кристаллах один из лучей поглощается значительно сильнее другого. Явление избирательного поглощения одного из лучей в кристалле называется дихроизмом. Например, кристаллы герапатита практически полностью по-глощают обыкновенный луч на длине 0,1 мм. Таким образом, падающий естественный свет, проходя через поляроид, становится полностью линейнополяризованным.

44. Анализ поляризованного света. Поляризатор и анализатор. Главная плоскость поляризатора (плоскость пропускания) и анализатора. Вывод закона Малюса в идеальном случае. Закон Малюса с учетом потерь, обусловленных поглощением и отражением света в поляризаторе и анализаторе.

2)Поляризаторами называются приборы, свободно пропускающие только те колебания светового вектора, которые параллельны од-ной плоскости. Эту плоскость мы будем называть плоскостью про-пускания поляризатора. Колебания, перпендикулярные этой плоскости, задерживаются полностью (идеальный поляризатор) или частично (неидеальный поляризатор). Поляризаторы, которые используются для анализа поляризован-ного света, называются анализаторами.

1) Рассмотрим следующий пример: на систему, состоящую из двух поляризаторов, плоскости поляризации которых повернуты относительно друг друга на угол ϕ, падает естественный свет интенсивно-стью I0. Пренебрегая отражением и поглощением, найдем ин-

тенсивность I света, прошедшего через эту систему.

Первый поляризатор пропустит только ту составляющую па-дающего светового вектора Е0i, которая параллельна плоскости пропускания поляризатора Epi = E0i cosϕi. В естественном свете присутствуют всевозможные ориентации светового вектора E. Так как интенсивность пропорциональна E2, то интенсивность прошедшего поляризатор света будет равна I=∑Eoi* cosϕi=Io 1\2Плоскость поляризации прошедшего света будет совпадать с плоскостью пропускания поляризатора yy′. Второй поляризатор (анализатор) пропустит только ту составляющую падающего светового вектора E0, которая параллельна плоскости пропускания анализатора E = E0 cosϕ. Так как интенсив-ность пропорцио-

нальна E2, то I= 1\2Io cosϕi

Таким образом, закон Малюса для поляризованного света без учета отражения и поглощения в поляризаторе и анализаторе записывается следующим образом:

изведению интенсивности поляризованного света (IP) на квадрат косинуса угла между плоскостями анализатора и поляризатора (угла между направлением колебаний, про- пускае-мых анализатором без учета потерь, и направлением колебаний светового вектора в луче, падающем на анализатор). Поворот анализатора вокруг поляризованного луча сопровожда-ется изменением интенсивности света, прошедшего через анализатор. Если ϕ = 90є (анализатор и поляризатор «скрещены»), то IA = 0.

Если ϕ = 0є, то IA = IP0, интенсивность прошедшего через анализатор света будет максимальной.

45. Тепловое излучение. Характеристики и свойства теплового излучения. Энергетическая светимость, испускательная способность тела и их взаимосвязь. Отражательная и поглощательная способности тел и их взаимосвязь.

Электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и оптических свойств этого тела, называется тепловым излучением Тепловое излучение имеет место при любой температуре выше 0 Ки характеризуется

сплошным спектром, положение максимума ко-торого зависит от температуры: при высоких температурах излуча-ются преимущественно короткие (видимые и ультрафиолетовые)электромагнитные волны, при низких — длинные (инфракрасные).Если расход энергии тела на тепловое излучение не восполняетсяза счет подвода к телу теплоты, то его температура понижается,а тепловое излучение уменьшается. Тепловое излучение — единственное излучение, которое может находиться в равновесии с веществом.

Основные количественные характеристики теплового излучения Поток энергии электромагнитного излучения Ф численно равен энергии, излучаемой телом в единицу времени по всем направлениям: Ф=Dw/dt

Энергетическая светимость (интегральная испускательная способность) RT — энергия электромагнитных волн, испускаемых за единицу времени с единицы площади поверхности тела по всем направлениям во всем диапазоне длин волн (от 0 до ∞): Rt=dW/ dSdt = =Ф d/ dSИндекс T указывает на то, что данная величина зависит от тем-пературы тела и определяется при конкретной температуре.

Испускательная способность (спектральная плотность энерге-тической светимости) rλ,T, rν,T — энергия электромагнитных волн, испускаемых за единицу времени с единицы площади поверхности тела по всем направлениям и приходящаяся на единичный спек-тральный интервал

длин волн или частот: , r λ T= dR T/ d λ ; r ν, T= dR T/ d ν; r T = = λ 2/ с

Индексы λ и ν указывают на то, что данная величина зависит, соответственно, от длины волны или частоты и определяется в дос-таточно узком интервале длин волн от λ до λ + dλ или частот от ν до ν + dν; с — скорость света.

Энергетическая светимость связана с испускательной способностью также соотношением:

Поглощательная способность (монохроматический коэффициент поглощения) тела ≤ — безразмерная величина, показывающая, какая доля энергии электромагнитных волн, падающих на поверхность тела, соответственно, в интервале

длин волн от λ до λ + dλ или частот от ν до ν + dν, поглощается им.

Отражательная способность тела ≤— безразмерная ве-

личина, показывающая, какая доля энергии электромагнитных волн, падающих на поверхность тела, соответственно, в интервале длин волн от λ до λ + dλ или частот от ν до ν + dν, отражается им.

Связь между поглощательной и отражательной способностями тел, не пропус-

кающих электромагнитное излучение:

46. Закон Кирхгофа для теплового излучения. Абсолютно черное тело; его модель; серое тело. Закон Стефана-Больцмана. Закон смещения Вина. Экспериментальные кривые зависимости испускательной способности абсолютно черного тела от длины волны излучения при различных температурах этого тела. Их анализ. Квантовая гипотеза и формула Планка. Связь между формулой Планка и законами Стефана-Больцмана и Вина.

Закон Кирхгофа

Отношение испускательной способности тела к его поглощательной способности не зависит от природы тела и равно испускательной способности абсолютно черного тела — rλ,T , которая является функцией температуры и длины волны

Экспериментальные кривые зависимости испускательной способности абсолютно черного тела от длины волны для различных температур приведены на рис. 2.1. Функция rλ*,T имеет большое значение в учении о тепловом излучении тел.

Абсолютно черное тело — тело, у которого во всем спектральном диапазоне и при любых температурах поглощательная способ-ность равна единице aλ,T = 1, aν,T = 1.

Серое тело — тело, у которого поглощательная способность меньше единицы и не зависит от длины волны (частоты), т. е. одинакова во всем спектральном диапазоне, и зависит только от темпера-

туры, материала и состояния поверхности тела: aλсер= aсер,

Закон Стефана–Больцмана. Энергетическая светимость абсолютно черного тела пропорциональ-

Закон смещения Вина. Длина волны λ, на которую приходится максимум испускательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре.

Из закона смещения Вина следует, что максимум функции rλ*,T по мере возрастания температуры смещается в область малых длин волн, а

при понижении температуры — в область больших длин волн. Таким образом, закон смещения Вина объясняет, почему при понижении температуры нагретых тел в их спектре начинает пре-обладать длинноволновое излучение (например, переход от белого каления к красному при остывании металла).

Формула Планка. Формула Планка описывает излучение абсолютно черного тела во всем спектральном диапазоне.

где c — скорость света; k — постоянная Больцмана; T

— температура излучающего абсолютно черного тела; h — постоянная Планка.

47. Элементы квантовой оптики. Явление внешнего фотоэффекта. Световая и вольт-амперная характеристика фотоэлемента при внешнем фотоэффекте. Три эмпирических закона внешнего фотоэффекта. Уравнение Эйнштейна для внешнего фотоэффекта. Работа выхода. Связь между задерживающим напряжением и максимальной кинетической энергии фотоэлектрона.

Внешним фотоэффектом называется явление испускания элек-тронов веществом под действием электромагнитного излучения. Внешний фотоэффект наблюдается в газах на отдельных атомах и молекулах (фотоионизация), в атомных ядрах (фотоядерные реакции) и в конденсированных средах

законы внешнего фотоэффекта.

1. Сила фототока насыщения, а следовательно, и количество фо-тоэлектронов, вылетающих в единицу времени с единицы поверхности вещества, прямо пропорциональны интенсивности падающего излучения, если его спектральный состав остается неизменным.

2. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты падающего монохроматического излучения и не зависит от его интенсивности.

3. Для каждого вещества существует минимальная частота ν0 (максимальная длина волны λ0), называемая красной границей фотоэффекта. Если частота падающего электромагнитного излучения меньше ν0, фотоэффект не наблюдается.

Используя закон сохранения энергии и предполагая, что каждый электрон поглощает один фотон, можно найти максимальную кинетическую энергию электронов, вылетевших из металла при освещении его поверхности монохроматическим светом частоты ν:

Данное уравнение получило название уравнения Эйнштейна.

Вольтамперная характеристика фотоэффекта. Ток насыщения. Задерживающее напряжение

Вольтамперной характеристикой называется зависимость фо-тотока iФ от напряжения U на электродах фотоэлемента при постоянном световом потоке Ф = const.

Если на анод фото-элемента подано достаточно большое положительное напряжение, то все вылетевшие из катода электроны достигнут анода, и фототок будет иметь максимальное значение для данного светового потока. Этот ток называется фототоком насыщения.

С уменьшением положительного напряжения на аноде уменьша-ется анодный ток, так как не все электроны, вылетевшие с катода, достигнут анода. Если подать отрицательное напряжение на анод (U < 0), то с увеличением напряжения (по абсолютной величине) фототок будет уменьшаться и при напряжении Uз станет равным нулю. Напряжение Uз, при котором фототок равен нулю, называют за-

держивающим напряжением.

Красная граница

Связь между задерживающим напряжением и максимальной кинетической энергии фотоэлектрона.