6.6.9 Статистические гипотезы

Величина отклонения выборочного показателя от его генерального параметра называется статистической ошибкой этого показателя или ошибкой репрезентативности. Статистические ошибки - это не ошибки возникающие в результате измерений. Их пояление обусловлено процессом отбора вариант из генеральной совокупности и к ошибкам измерений отношения не имеют. Чем сильнее варьирует признак, тем больше при прочих равных условиях будет ошибка выборочных показателей и наоборот.

По известным значениям выборочных характеристик можно установить интервал, в котором с той или иной вероятностью находится величина генерального параметра. Вероятности, признанные достаточными для уверенных суждений о генеральных параметрах на основании выборочных показателей, называются доверительными.

Решение той или иной задачи, как правило не обходится без сравнений. О преимуществе одной из сравниваемых групп судят обычно по разности между выборочными средними. Но эта оценка тоже может носить случайный характер. Чтобы решить вопрос об истинной значимости различий,наблюдаемых между выборочными средними исходят из статистических гипотез - предположений или допущений о неизвестных генеральных параметрах, выражаемых в терминах вероятности, которые могут быть проверены на основании выборочных показателей.

Применяется так называемая нулевая гипотеза (), то есть, предположение о том, что между генеральными параметрами сравниваемых групп разница равна нулю и различия, наблюдаемые между выборочными показателями, носят исключительно случайный характер.

Противоположная или альтернативная гипотеза, наоборот, исходит из предположения, что между генеральными параметрами сравниваемых групп разница не равна нулю.Статистические гипотезы могут исходить и из других предположений.

Истинность принятой гипотезы проверяется с помощью критериев значимости, или достоверности, то есть, специально выработанных случайных величин, функции распределения которых известны. Обычно для каждого критерия составляется таблица, в которой содержатся критические точки, отвечающие определенным числам степеней свободы () и принятым уровням значимости .

Уровни значимости - значение вероятности, при котором различия, наблюдаемые между выборочными показателями, можно считать несущественными, случайными. В исследовательской работе обычно принимается 5% уровень значимости, который соответствует вероятности =0,05 и нормированное отклонение, если распределение критерия нормально. Если окажется, что, то нулевая гипотеза сохраняется, иначе отвергается.

Рассмотрим гипотезу о равенстве средних арифметических исходных генеральных совокупностей. В рассмотрении участвуют две выборки и их параметры: объем выборки и средняя арифметическая (идля первой выборки и и для второй). Нулевая гипотеза предполагает, что .

Имеется ли различие между этими средними значениями? Чтобы определить какой характер носит это различие используют критерий Стьюдента. Вычисленное значение критерия будет определено по формуле:

, (6.98)

. (6.99)

Вычисленное значение критерия сравниваем с критической точкой, взятой из таблицы распределения Стьюдента в соответствии с выбранным уровнем значимости и числом степеней свободы . Если больше табличного значения, то гипотезу о равенстве средних следует отвергнуть. Это будет означать, что различие средних нельзя считать случайным.

Теперь рассмотрим гипотезу о равенстве дисперсий исходных генеральных совокупностей. В рассмотрении участвуют две выборки и их параметры: объем выборки и дисперсия (идля первой выборки и и для второй). Нулевая гипотеза предполагает, что . Воспользуемся критерием Фишера (отношение большей из дисперсий к меньшей). Вычисленное значение критерия Фишера сравниваем с критическим значением, взятым из таблицы распределения Фишера в соответствии с уровнем значимости и степенями свободы и. Если вычисленное значение критерия больше табличного, то различие выборочных дисперсий следует признать значимым.

Чтобы проверить, распределен ли варьирующий признак по нормальному закону, поступают следующим образом. Пусть элементы выборки распределены по - интервалам, причем - тому интервалу () соответствуе частота . Для проверки гипотезы о каком - либо распределении случайной величины используют критерий (критерий Пирсона).

Вычисленное значение критерия определяется по формуле: , (6.100)

где - относительная частота соответствующая - ому интервалу, - теоретическая частота, соответствующая - ому интервалу. Правило вычисления и определение числа степеней свободы зависит от вида теоретического распределния и способа оценки его параметров.

Сравним эмпирическое распределение с нормальным.

, (6.101)

где и - левая и правая границы - ого интервала, - плотность нормального распределения. Для упрощения вычислений можно заменить интеграл в правой части этого равенства произведением длины промежутка интегрирования и значения функции в средней точке интервала, то есть,

. (6.102)

В таблице распределения находим критическую точку, соответствующую выбранному уровню значимости и числу степеней свободы (если и не определяются по имеющимся данным, а известны заранее, то число степеней свободы ). Если вычисленное по формуле значение критерия больше табличного, то на уровне значимости прверяемая гипотеза должна быть отвергнута.

Можно поступить еще и так. Пусть - абсолюное значение частоты - ого интервала. Можно сравнить частоты теоретические и эмпирические. В этом случае

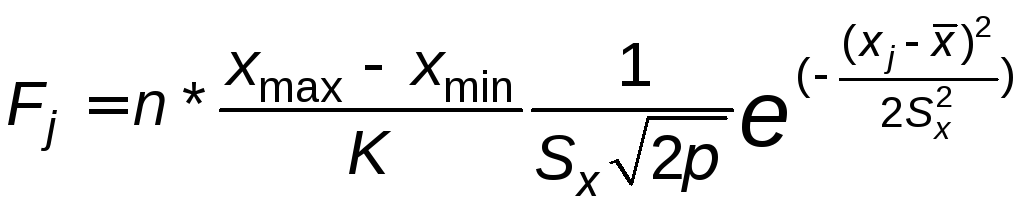, (6.103)

где - объем выборки.

Для нормального распределения характерно совпадение по абсолютной величине средней арифметической, медианы и моды. Для этого вида распределения характерно то, что на равные интервалы, измеряемые нормированным отклонением от центра распределения, приходится равное число вариант.

Кривую нормального распределения характеризуют величины асимметрия () и эксцесс.(). Эти величины для рассматриваемой выборки можно определить, зная выборочные характеристики: среднюю арифметическую и дисперсию.

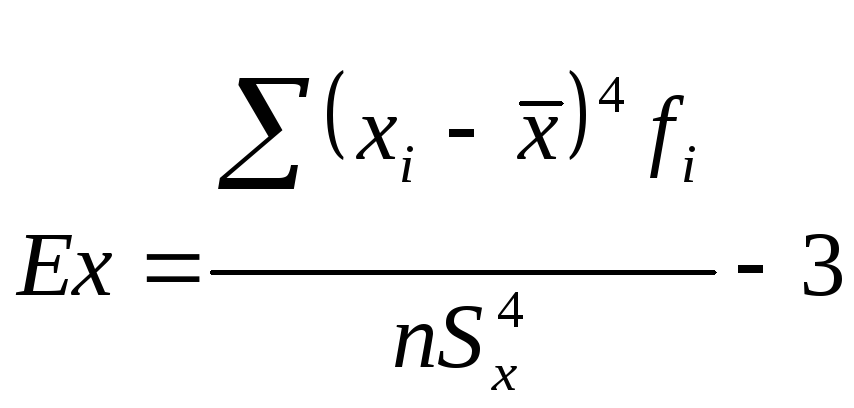, . (6.104)

Можно оценить статистические ошибки выборочных характеристик. Для выборочной средней , для асимметрии , для эксцесса . И нулевая гипотеза о том, что эмпирическое распределение нормально будет отвергаться, если и .

Контрольные вопросы

1. Сформулируйте определение математической модели.

2. Перечислите основные численные методы решения технических задач.

3. Приведите примеры моделей, приводящих к необходимости численного дифференцирования и интегрирования функций.

4. Приведите примеры моделей, описываемых обыкновенными дифференциальными уравнениями.

5. В чем состоит идея методов Рунге-Кутта и прогноза и коррекции?

6. Приведите примеры моделей, описываемых дифференциальными уравнениями в частных производных.