6.6.2 Графическое изображение вариационных рядов. Эмпирическое распределение

При построении графика зависимости частот от значений вариант безинтервального вариационного ряда по оси абцисс откладываются значения классов (вариант) по оси ординат - частоты. В результате будет построена геометрическая фигура в виде многоугольника. Полученный график называют полигоном распределения частот.

При построении графика зависимости частот от значений вариант интервального вариацинного ряда по оси абцисс откладывают границы классовых интервалов, по оси ординат - частоты. В результате - гистограмма распределения частот. Можно поступить иначе: по оси абцисс отложить срединные значения классов (), по оси ординат частоты для указанного класса.

Вариационная кривая - это сглаженные значения полигона.

Совокупность значений и соответствующих им частот называется эмпирическим распределением.

6.6.3 Средние величины и показатели вариации

Вариационные ряды и их графики дают наглядное представление о том, как варьирует тот или иной количественный признак. Но они недостаточны для полной характеристики статистической совокупности. Количественные показатели, которые (логически и теоретически обоснованы) позволяют судить о качественном своеобразии варьирующих объектов и сравнивать их между собой, называются статистическими характеристиками.

В отличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать группу однородных вариант одним (средним) значением. И хотя средние абстрагируют нас от конкретных вещей, они вполне понятны и ощутимы. Средний рост, средняя масса …(то есть, здесь уравновешиваются все индивидуальные отклонения и появляется качественное своеобразие группового объекта).

По определению Гаусса, истинной средней служит такая величина, сумма квадратов отклонений от которой обладает нименьшим значением.

, (6.90)

где - средняя величина, - варианта, - объем выборки, - величина, определяющая вид средней.

Средние величины могут характеризовать только однородную массу вариант (если это не так, следует сгруппировать варианты в отдельные качественно однородные группы и вычислять групповые средние).

‑средняя гармоническая. В этом случае . В некоторых случаях для усреднения количественных признаков используется такой тип средней.

‑средняя квадратическая. При выражении количественных признаков вариант мерами площади более точной усредненной характеристикой будет средняя квадратическая .

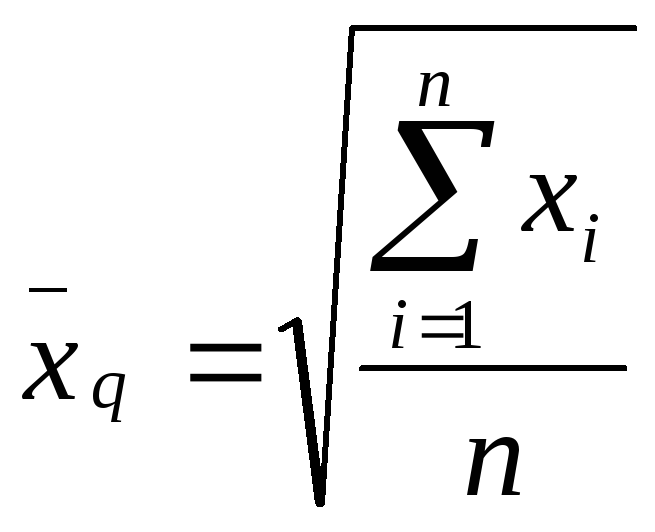‑средняя кубическая. Более точная средняя характеристика, в тех случаях, когда варьирующий признак выражен в объмных единицах.

.

Средняя геометрическая является более точной характеристикой при определении средних прибавок или при увеличении линейных размеров тел, прироста численности популяции за определенный промежуток времени.

.

‑средняя арифметическая. Эту величину рассотрим подробнее.

6.6.4 Средняя арифметическая и ее свойства

‑ средняя арифметическая является центром распределения, вокруг которого группируются все варианты статистической совокупности.

. (6.91)

Если рассматривается интервальный вариационный ряд, то средняя арифметическая, называемая взвешенной, вычисляется по формуле

, (6.92)

где - частота - ого класса, , - количество классовых интервалов. Рассмотрим свойства средней арифметической.

Свойство 1.Если каждую варианту совокупности уменьшить или увеличить на какое-то произвольное положительное число А, то и средняя арифметическая уменьшится или увеличится на столько же.

Свойство 2.Если каждую варианту разделить или умножить на одно и тоже число А, то и средняя арифметическая изменится во столько же раз.

Свойство 3.Сумма произведений отклонений вариант от их средней арифметической на соответствующие им частоты равна нулю.

Свойство 4.Сумма квадратов отклонений вариант от их средней арифметической меньше суммы квадратов отклонений тех же вариант от любой другой величины А, не равной средней арифметической.

Размахвариациихарактеризует варьирование признака в совокупности.

Рассмотрим еще две характеристики выборочной совокупности: дисперсию и среднее квадратическое отклонение. Эти величины характеризуют не только величину, но и специфику варьирования признака.