6.2.7 Формула трапеций

При п=1 из формулы (6.31) имеем:

Тогда по формуле (6.32) на отрезке получаем интеграл:

(6.33)

Формула (6.33) дает один из простейших способов вычисления определенного интеграла и называется формулой трапеций. Действительно, при п=1 подынтегральная функция заменяется интерполяционным многочленом Лагранжа первой степени (т.е. линейной функцией), а геометрически это означает, что площадь криволинейной фигуры заменяется площадью трапеции.

Распространяя формулу (6.33) на все отрезки разбиения, получим общую формулу трапеций для отрезка :

(6.34)

Если аналитическое выражение для подынтегральной функции известно, может быть поставлен вопрос об оценке погрешности численного интегрирования по формуле (6.34) (погрешность метода).

В этом случае имеется ввиду, что

где ‑ остаточный член квадратурной формулы (6.34). Формулу остаточного члена получим вначале для отрезка. Имеем:

_{откуда следует, что естественно рассматривать R как функцию шага h: R=R(h). Заметим, что R(0)=0.}

_{Продифференцируем R(h) по h:}

Заметим, что . Далее:

(6.35)

Определим R, последовательно интегрируяна отрезке:

откуда с учетом (6.35) имеем:

. (6.36)

Применяя к (6.36) обобщенную теорему о среднем, получаем:

(6.37)

где изависит отh. Далее

откуда с учетом (6.37) и обобщенной теоремы о среднем имеем:

где

Таким образом, погрешность метода при интегрировании функции на отрезке по формуле (6.34) имеет величину:

(6.38)

Из формулы (6.38) видно. что при формула (6.34) дает значение интеграла с избытком, а при‑ с недостатком. Можно показать, что при распространении оценки (6.38) на весь отрезок интегрированияполучается формула:

Учитывая, что , найден следующий окончательный вид для оценки погрешности метода интегрирования по формуле трапеций:

(6.39)

где .

Пример 6.3.

Используем формулу трапеций для n = 2 и n = 4.

Таблица 6.3

xi	0				1
f(xi)	0				1

6.2.8 Формула Симпсона

При п=2 из формулы (6.31) последовательно имеем (i=0, 1, 2):

Тогда с учетом (6.32) получим на отрезке :

т.е.

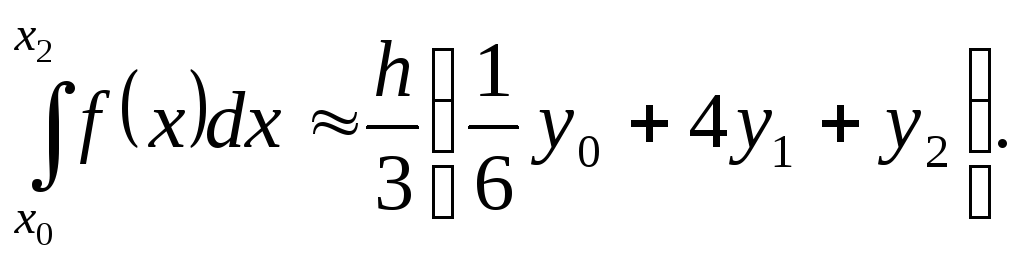(6.40)

Геометрически, в соответствии со смыслом интерполяционной формулы Лагранжа при п=2, использование формулы (5.40) означает замену подынтегральной функцииf(x) параболойL₂(x), проходящей через точкиM_i(x_i, y_i) (i=0, 1, 2).

Если считать, что п– четное (n=2m), то применяя формулу (6.40) последовательно к каждой паре частичных отрезков(i=1, 2, …, m) получим:

(6.41)

Формула (6.41) называется формулой Симпсона.

Оценка остаточного члена формулы Симпсона дается формулой:

или

(6.42)

где 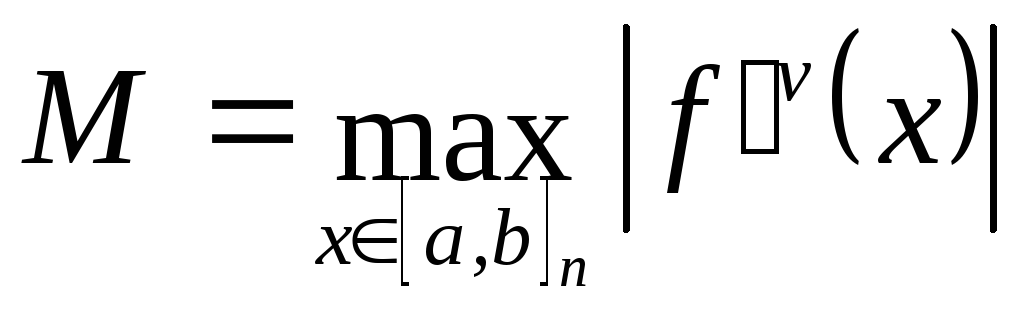. Как следует из оценки, формула Симпсона, оказывается точной для полиномов до третьей степени включительно (т.к. для этих случаев производная четвертого порядка равна нулю). Формула Симпсона обладает повышенной точностью по сравнению с формулой трапеций. Это означает, что для достижения той же точности, что и по формуле трапеций, ней можно брать меньшее число отрезков разбиения.

Укажем простой практический прием позволяющий прогнозировать требуемое число отрезков разбиения по заданной точности .

Пусть задана предельная допустимая погрешность интегрирования Желая иметьс учетом оценки (6.42) достаточно потребовать

откуда

т. е. (6.43)

Формула (6.43) позволяет оценить величину шага, необходимую для достижения заданной точности.