
СпецкурсПГС
.pdf10
опросам, хотели бы куда-то переехать из столь долгожданных новых квартир. Их легко понять: выходишь из подъезда - перед тобой стена с окнами – гвоздями, справа – такая же стена, слева
– тоже. Неуютно. В природе за долгую эволюцию человек не встречался с такими агрессивными полями и нет механизма, от них защищающего. Не потому ли урбанизация, по данным ВОЗ (Всемирная охрана здоровья – международная общественная организация), неуклонно ведет к росту численности психических заболеваний.
Деревянные панели в служебных помещениях, стенки под дерево заполняют все плоскости холлов, комнат и коридоров многих квартир. Вроде бы порядок. Только вот бежать из такого холодного дома хочется.
Каким же образом можно избежать подобных неприятностей? Главное – создать среду в соответствии с законами восприятия окружающего нашими органами чувств. В идеале она не должна отличаться от природной среды. Тогда горожанину не захочется бежать из города. Прежде всего нельзя строить такие гомогенные да еще и агрессивные массивы. Их разбить нетрудно. Жидкому бетону можно придать любую форму. Яркая окраска, веселые балкончики, башенки, шпили. Очевидно, скоро мы к этому придем. Тут за образец можно взять Зеленоград, Новосибирский Академгородок, когда вроде бы стандартные дома «прячутся», удачно вписываясь среди ландшафта и деревьев. Норильск, Киев (Троещино) – ярко окрашенные косыми полосами стены крупнопанельных зданий. Хорошо применить фонтаны, скульптуры и др. малые архитектурные формы. Все это должно быть выполнено в соответствии с законами автоматии саккад, где все углы остры, как в природе.
А в интерьерах помещений важно, чтобы не было однообразия. Здесь смогут помочь любые репродукции: эстамп, графика, скульптура. Для этой цели можно привлечь комнатные цветы и растения, особенно большие, разрушающие гомогенность.
Прежде всего, это важно в интерьере детской. Замечено, что если ребенок от 3 до 18 месяцев пребывает в серой, скучной, однородной среде, это отражается на его развитии. Он не видит мир таким, каким он есть. Краски тускнеют. Причина в том, что младенец видит в несколько раз хуже взрослого. Без яркого, контрастного окружения трансформируется заложенная природой связь между сенсорным и зрительным аппаратами. Став взрослым, такой человек может быть умственно отсталым, а к ряду профессий (летчик, космонавт, оператор и др.) просто непригодным. Об этом мы как раз и говорили в начале этой лекции (опыт с обезьянами).
Еще один важный момент. Нужно периодически делать перестановку мебели, перевешивать картины, гравюры. В этом кроется огромный психологический фактор. Меняя среду, мы воздействуем на свой эмоциональный настрой. А если внести новый элемент – цветок, свечу, салфетку, положить на один диван подушку – эффект будет усилен. Так, вроде бы незаметно, мы можем бороться не только с гомогенными, но и агрессивными полями [2] .
11
Лекция № 3
ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ СТРОИТЕЛЬНОЙ СВЕТОТЕХНИКИ
Основные понятия, величины, единицы
Всякое тело, обладающее температурой выше абсолютного нуля, излучает в окружающее пространство энергию, называемую лучистой энергией (Qe).
Количество энергии, посылаемое источником в единицу времени, называется интенсивностью излучения или лучистым потоком:
Ф |
|
|
dQe |
, [Вт], |
(1) |
е |
|
||||
|
|
dt |
|
||
где dt – бесконечно малый промежуток времени, в течение которого излучение является |
|||||
равномерным. |
|
|
|
|
|
Оптическая часть электромагнитного спектра лучистой энергии включает три состав- |
|||||
ляющие: |
|
|
|
|
|
ультрафиолетовую область излучения с длиной волны = 280 – 400 нм; |
|||||
видимую область излучения с длиной волны |
= 400 – 780 нм; |
||||
инфракрасную область излучения с длиной волны |
= 780 нм – 1 мм. |
||||
Действуя на глаз, излучения, имеющие различную длину волны, вызывают ощущения |
|||||
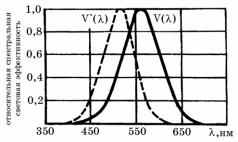
того или иного цвета. Чувствительность глаза к тому или |
|||||
иному цвету различна (рис. 4). Средний человеческий |
|||||
глаз наиболее чувствителен при дневном зрении к желто- |
|||||
зеленому излучению с длиной волны = 555 нм. |
|||||
|
|
Мощность светового излучения (видимая область |
|||
спектра), оцениваемая по световому ощущению, которое |
|||||
она производит на средний человеческий глаз, называет- |
|||||
ся с в е т о в ы м п о т о к о м (F). |
|||||
|
|
Единица измерения светового потока – люмен |
|||
Рис. 4. Кривые относительной (лм), т.е. световой поток, излучаемый в единичном те- |
|||||
спектральной световой эффек- |
лесном угле равномерным точечным источником света |
||||||
тивности излучений для днев- |
силой в 1 канделу. |
|
|||||
ного |
V( ) |
и |
ночного |
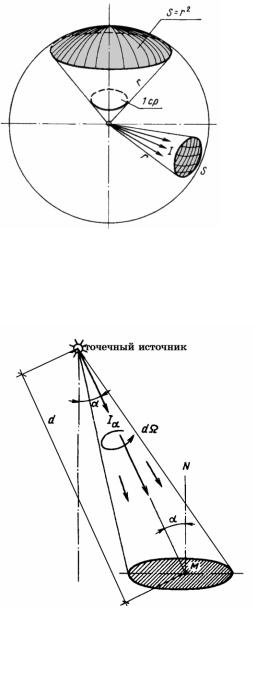
Телесный угол ( ) – часть пространства, ограни- |
|||
V ( ) зрения. |
|
|
ченная конической или пирамидальной поверхностью с |
||||
Измеряется в стерадианах (ср). |
вершиной в точке расположения источника излучения. |
||||||
|
Sсф |
|
|
||||
|
|
|
|
щ |
, [ср] |
(2) |
|
|
|
|
|
R2 |
|||
|
|
|
|
|
|
|
|
где Sсф – площадь |
сферической поверхности, |
на которую опирается |
телесный угол |
||||
(рис. 5); |
|
|
|
|
|
|
|
R – радиус этой сферической поверхности.
Оценка светового действия источника в каком-либо направлении производится величиной, называемой с и л о й с в е т а (I) – пространственная (угловая) плотность светового потока источника света, излучаемого в данном направлении. Измеряется в канделах (кд).
I |
dF |
, [кд] |
(3) |
|
|||
|
dщ |
|
|
Кандела представляет собой интенсивность света, испускаемого в перпендикулярном направлении с площади в 1 / 600000 м2 черного тела при температуре затвердевания платины Т=2045 К и давлении 101325 Па.
12
О с в е щ е н н о с т ь (E) - поверхностная плотность светового потока dF, падающего на данную поверхность dS. Измеряется в люксах (лк).
E |
dF |
, лк. |
(4) |
|
|||
|
dS |
|
|
Люкс представляет собой освещенность поверхности, на 1 м2 которой падает и равномерно распределяется на ней световой поток, равный 1 лм.
Для точечных источников света (рис. 6)
|
E |
I cosб |
, лк, |
(5) |
|
|
|||
|
|
d2 |
|
|
|
d – расстояние от источника до освещаемой поверхно- |
|||
Рис. 5. Схема к определению |
сти, м; |
|
||
|
- угол между нормалью к поверхности и направлени- |
|||
телесного угла
ем силы света.
Я р к о с т ь (L) представляет собой поверхностную плотность силы света в заданном направлении. Определяется отношением силы света бесконечно малого элемента светящейся поверхности (по направлению к глазу наблюдателя) к площади проекции этого элемента на плоскость, перпендику-
лярную тому же направлению:
Рис. 6. Схема к определению освещенности от точечного источника света
L |
dI |
, [кд / м2], |
(6) |
|
|||
|
ds cosв |
|
|
s – площадь светящейся поверхности, м2;
- угол между направлением линии зрения и нормалью к светящейся поверхности, град;
Яркость – световая величина, которая непосредственно воспринимается глазом.
Яркости некоторых светящихся тел представлены в таблице 1.
Это основные величины и единицы, которые используются в светотехнике. В строительной светотехнике при проектировании естественной световой среды в зданиях использовать абсолютные критерии неудобно по той причине, что источником излучения света является небосвод. Параметры этого природного излучения постоянно меняются в течение года, сезона и суток. Поэтому удобнее в этом случае использовать относительные критерии.
Яркости различных светящихся тел
|
|
Таблица 1 |
№ |
Источник |
Яркость, кд / м2 |
1 |
Ночное безлунное небо |
Около 1 10-4 |
2 |
Полная луна, видимая сквозь атмосферу |
2,5 103 |
3 |
Пламя обычной стеариновой свечи |
5 103 |
4 |
Ясное дневное небо в зените в полдень |
(2,5 – 4) 103 |
5 |
Облачное небо в зените в полдень |
(7 – 8) 103 |
6 |
Спираль газонаполненной лампы накаливания |
5 106 |
7 |
Диск Солнца |
1,5 109 |

13
В связи с этим критерием оценки переменного естественного освещения служит величина, называемая КОЭФФИЦИЕНТОМ ЕСТЕСТВЕННОЙ ОСВЕЩЕННОСТИ (КЕО, е), который
показывает какую долю освещенность в данной точке помещения составляет от одновременной наружной освещенности горизонтальной поверхности на открытом месте при пасмурном (облачность 8 – 10 баллов) небосводе и выражается отношением
е |
Е |
в |
100, %, |
(7) |
|
Е |
н |
||||
|
|
|
где Ев – освещенность в расчетной точке внутри помещения, лк; Ен – одновременная освещенность этой же точки под открытым небосводом, лк.
Одновременно с этим понятием используется понятие ГЕОМЕТРИЧЕСКИЙ КОЭФФИ-
ЦИЕНТ ЕСТЕСТВЕННОЙ ОСВЕЩЕННОСТИ ( ) – отношение естественной освещенности,
создаваемой в рассматриваемой точке заданной плоскости внутри помещения светом, прошедшим через незаполненный световой проем и исходящим непосредственно от равномерно яркого неба (Евп) к одновременному значению наружной горизонтальной освещенности под открытым полностью небосводом (Ено), при этом участие прямого солнечного света в создании той и другой освещенности исключается; выражается в процентах:
е |
Е |
вп |
100, %. |
(8) |
|
Е |
но |
||||
|
|
|
Законы архитектурной светофизики
Освещенность в какой-либо точке помещения создается световым потоком, который излучается с участков небосвода, видимых из данной точки через светопроемы, расположенные в ограждающих конструкциях здания. При этом возникает вопрос, от каких параметров зависят светотехнические показатели и каким образом их можно определить. Это позволяет сделать четыре основных закона строительной светотехники, которые формируют теоретическую базу данной науки.
1. Закон проекции телесного угла.
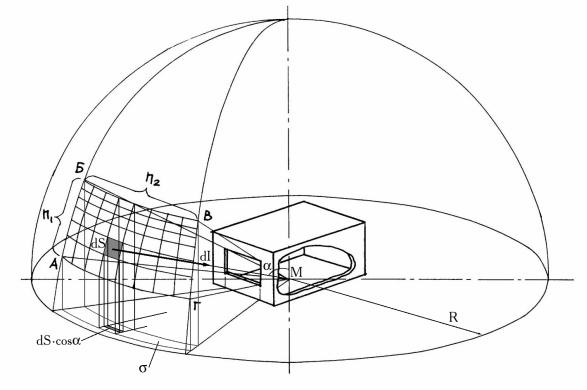
Поместим помещение с расчетной точкой М под небосвод, который представляет собой полусферу единичного радиуса (рис. 7). Причем точка М совпадает с центром полусферы.
Для упрощения вывода закона примем следующие три допущения:
1)яркость неба во всех точках одинакова;
2)влияние отраженного света от внутренних поверхностей помещения не учитывается;
3)оконное заполнение светопроема отсутствует.
Освещенность в точке М создается видимым из т. М через проем сферическим прямоугольником АБВГ (рис. 7) площадью S. В этом прямоугольнике вырежем бесконечно малый точечный элемент dS с силой света dI. На основании формулы (6) определяем яркость этого элемента
L dI откуда dI = L dS. dS
Поскольку направление излучения от элемента dS до точки М перпендикулярно элементарной площадке, то = 0 и cos = 1.
Освещенность в т. М согласно формуле (5) для точечного источника света определится следующим образом:
EM |
|
dI cosб |
. |
|
|||
|
|
R2 |
|
Подставляя dI из предыдущего выражения, получаем
EM |
|
L dS cosб |
. |
|
|||
|
|
R2 |
|
14
Однако, величина dS / R2 = d , согласно формулы (2), а величина dS cos / R2 = d есть проекция элементарного телесного угла на освещаемую плоскость. При интегрировании до конечных размеров светопроемов d = .
Таким образом,
ЕМ = L . |
(9) |
На основании этого выражения закон проекции телесного угла можно сформулировать следующим образом.
Освещенность в какой-либо точке поверхности помещения, создаваемая равномерно светящимся небосводом, прямо пропорциональна яркости неба L и площади проекции телесного угла , в пределах которого из данной точки виден участок неба, на освещаемую поверхность.
На основании этого закона можно вычислить значение КЕО в точке М. Освещенность в этой точке под открытым небосводом с использованием формулы (9) будет равна:
Ен = L н = L R2 ,
т.к. площадь проекции всей полусферы на горизонтальную плоскость н = R2 , а при единичном радиусе н = . Тогда, Ен = L . Подставляем значения двух освещенностей в формулу (7)
е |
ЕМ |
100 = |
L у |
100 = |
у |
100, |
(10) |
|
|
||||||
|
Ен |
L р |
|
р |
|
||
т.е. при равноярком небосводе величина КЕО прямопропорциональна площади проекции телесного угла светопроема.
Рис. 7. Схема к закону проекции телесного угла
Практическое значение этого закона очень велико: пользуясь им, можно сравнивать освещенности, создаваемые одним и теме же светопроемом, расположенным различно относительно рабочей плоскости, а также определять светотеневой рисунок на объемных объектах и деталях под открытым небосводом в пасмурный день.
На основе этого закона разработан ряд графических и аналитических методов расчета естественного освещения (в частности, метод Данилюка), получившие широкое распространение в нашей и мировой архитектурной практике.
15
2. Закон светотехнического подобия
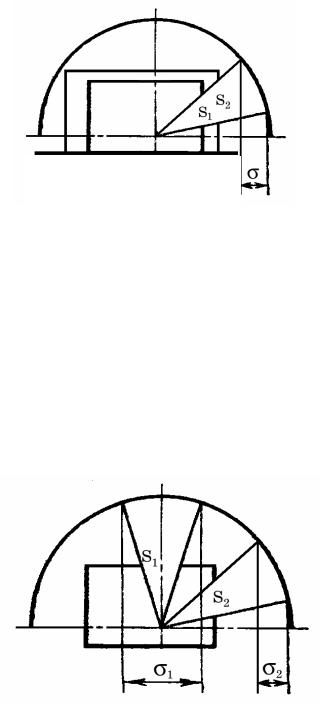
Рассмотрим освещенность в точке М, создаваемую несколькими светящимися поверхностями, имеющими яркости L1, L2, …, Lк и площади проекции телесных углов на освещаемую плоскость 1, 2,…, к. Тогда освещенности от этих поверхностей в данной точке будут равны:
Е1 = L1· 1; Е2 = L2· 2; ….; Ек = Lк· к.
Рис. 8. Схема к закону светотехнического подобия
Условие, когда эти поверхности создадут равные освещенности, т.е. Е1 = Е2 = … = Ек, будет
соблюдено, если L1· 1 = L2· 2 = … = Lк· к.
Если принять полусферу равномерной ярко-
сти, то 1 = 2 = … = к.
Отсюда видно, что светящиеся поверхности
– светопроемы – могут иметь различные размеры при одинаковом значении площади проекции телесного угла, описанного из т. М по контурам этих проемов.
Из всего этого следует, что освещенность в
точке от светящейся поверхности зависит не от абсолютных ее размеров, а от относительных.
Или, светящиеся равнояркие поверхности разных размеров могут создать в точке одинаковую освещенность, если площади проекции их телесных углов, описанных из точки по их контуру, будут равны. На схеме (рис. 8) представлены два светопроема. Хотя абсолютные их размеры различны S2 S1, но 1 = 2 = , поэтому и освещенности от этих двух светопроемов будут равны. Это и есть формулировки закона светотехнического подобия.
3. Закон эффективности светопроемов
Светопроемы, плоскость остекления которых располагаются параллельно освещаемой плоскости, имеют наибольшую световую активность по отношению к светопроемам, имеющим какой-либо угол наклона.
|
На схеме (рис. 9) представлено помеще- |
|
|
ние с двумя одинаковыми по размерам свето- |
|
|
проемами, один из которых расположен в стене, |
|
|
другой в покрытии. Причем, расстояние от рас- |
|
|
четной точки до центров проемов равны. Из |
|
|
схемы видно, при равенстве размеров проемов |
|
|
S1 = S2, проекции телесных углов на освещае- |
|
|
мую плоскость различны 1 2, поэтому осве- |
|
|
щенность от светопроема, расположенного в по- |
|
|
крытии, будет гораздо больше освещенности от |
|
|
светопроема, расположенного в стене. Отсюда |
|
|
следует, что зенитные фонари обладают наи- |
|
|
большей световой активностью, т.к. плоскость |
|
Рис. 9. Схема к закону эффективности |
||
их остекления параллельна освещаемой плоско- |
||
светопроемов |
||
сти. |
||
|
||
|
Практическое значение этого закона заключается в том, что сразу можно определить относительную световую эффективность светопроемов одинаковой площади, расположенных под различными углами наклона.
16
4. Закон сложения освещенностей
Поскольку освещенность плоскости величина скалярная, то освещенность в данной
точке помещения от нескольких светопроемов равна сумме освещенностей от каждого светопроема в отдельности.
Т.е. Ев = Е1 + Е2 +…+ Ек . Если это выражение подставить в формулу определения КЕО (7), то получим
|
Е |
в |
|
Е1 |
Е2 |
... Ек |
|
|
Е1 |
|
Е |
2 |
|
Е |
к |
|
|
|
|
|
|
|
|
|
|
|
|
... ек . |
(11) |
||||||||||
е |
|
100 |
|
|
|
100 |
|
|
|
... |
|
е2 |
|||||||
|
|
Ен |
|
Ен |
|
|
100 е1 |
||||||||||||
|
Ен |
|
|
|
|
|
Ен |
|
Е |
н |
|
|
|
||||||
Понятно, что в большинстве случаев в помещениях имеется несколько светопроемов и этот закон позволяет определить в любой точке помещения суммарное значение КЕО от всех проемов.
Сущность метода расчета геометрического КЕО по А.М. Данилюку
На базе рассмотренных законов архитектурной светофизики разработано несколько методов расчета освещенности. Однако наиболее простым и удобным в практике архитектурностроительного проектирования является графоаналитический метод расчета геометрического КЕО, который разработал в 20 – 30 годы прошлого века А.М. Данилюк. Идея этого метода состоит в следующем.
Источником излучения при естественном освещении является небосвод. Данилюк представил его в виде полусферы, поверхность которой он разбил на 10000 площадок двумя группами (100 100) плоскостей. Первая группа – плоскости, проходящие через основной диаметр. Вторая группа – плоскости, проходящие параллельно основному вертикалу полусферы, проходящему через ее центр, а также перпендикулярно первой группе плоскостей. Причем, разбивка осуществлялась таким образом, чтобы проекция телесного угла каждой площадки была одинакова. Следовательно, на основе закона проекции телесного угла, каждая площадка создает одинаковую освещенность в центре полусферы и на основе этого можно принять, что из центра каждой площадки исходит по одному световому лучу. Тогда освещенность расчетной точки, находящейся под открытым небосводом, можно считать равной Eн = 10000 лучей (или единиц).
Помещаем эту расчетную точку в помещение, например, с одним светопроемом. Большая часть лучей света не будет доходить до расчетной точки, т.к. ограждения помещения не светопрозрачны. Только лишь некоторое количество лучей будет проходить через проем в данную точку. А именно от прямоугольника АБВГ (рис. 7), являющегося основанием телесного угла светопроема с вершиной в расчетной точке М. Чтобы определить количество лучей, проходящих от участка небосвода АБВГ через проем в помещение, необходимо определить площадь участка АБВГ в лучах, для чего количество лучей по вертикали БВ (n1) умножается на количество лучей по горизонтали АБ(n2).Тогда освещенность в расчетной точке помещения определиться
Ев = n1 n2 лучей (или единиц),
где n1 - количество лучей, проходящих в расчетную точку через проем на разрезе помещения;
n2 - количество лучей, проходящих в расчетную точку через проем (или через проемы) на плане помещения.
Итак, имея освещенность в расчетной точке внутри помещения Ев и освещенность этой же точки под открытым небосводом Ен, можно определить геометрический коэффициент естественной освещенности, используя формулу (8):
|
Е |
В |
100 |
n1 n2 |
100 0.01 n1 n |
2 , %. |
(12) |
Е |
|
10000 |
|||||
|
Н |
|
|
|
|||
Поскольку Данилюк был архитектором, то он знал, что архитекторы постоянно работают с планами и разрезами. Поэтому разбитая на площадки полусфера была сначала спроецирована
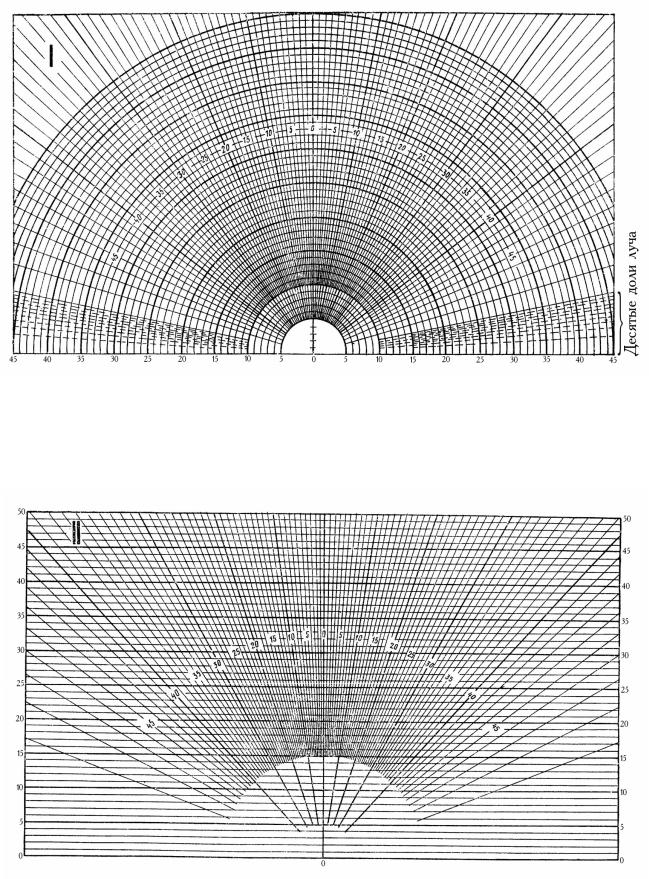
17
Рис. 10. График І А.М. Данилюка для подсчета количества лучей, проходящих через боковые светопроемы на поперечном разрезе помещения
Рис. 11. График ІІ А. М. Данилюка для подсчета количества лучей, проходящих через боковые светопроемы на плане помещения и через верхние светопроемы на продольном разрезе
18
на вертикальную плоскость, где первая группа плоскостей превратилась в радиальные линии (рис. 10), а вторая – в концентрические полуокружности. Таким образом получился график І.
Затем полусфера была спроецирована на горизонтальную плоскость, где радиальные линии остались, а вторая группа плоскостей превратилась в горизонтальные линии. Таким образом получился график ІІ (рис. 11).
Итак, чтобы получить значение геометрического КЕО, необходимо расчетную точку на разрезе помещения совместить с графиком І и подсчитать количество лучей n1, проходящих через светопроем. Затем совместить план помещения с графиком ІІ и подсчитать количество лучей n2, проходящих через проемы. По формуле (12) нетрудно определить величину геометрического КЕО.
19
Лекция № 4
Основные положения теории светового поля
Прогрессивным моментом при проектировании световой среды помещений является переход к оценке световой среды по пространственным характеристикам светового поля. Это прежде всего связано с тем, что существующий критерий оценки – коэффициент естественной освещенности (КЕО) – плоскостная характеристика, которая может оценивать освещение объектов, находящихся в плоскости. Однако он не может в достаточной степени оценить условия распределения световых потоков по объемным объектам с рельефной поверхностью.
Использование КЕО в качестве нормируемого параметра приводит к раздельному нормированию бокового и верхнего естественного освещения, естественного и искусственного освещения. Это приводит к значительным погрешностям при оценке систем естественного и совмещенного освещения и, как результат, к неоправданным энергетическим и экономическим затратам. Данное положение подтверждается некоторыми работами по приложению теории светового поля к проектированию систем естественного освещения зданий. Многие исследователи утверждают то, что оценка световой среды должна осуществляться при помощи комплекса количественных и качественных параметров светового поля.
Световое поле – это область пространства, из одной точки которого в другую осуществляется перенос световой энергии.
Эффективную оценку условий освещения можно осуществлять следующими основными пространственными характеристиками светового поля [15].
Количественные характеристики:
Средняя сферическая освещенность (Е4 ) – средняя плотность светового потока на поверхности сферы, радиус которой стремится к нулю. Эта величина является функцией точки, т.е. как сферу ни поворачивай вокруг своего центра, значение освещенности будет оставаться одним и тем же. Если при плоскостной характеристике, например, горизонтальной освещенности, боковые светопроемы имеют малую освещенность поскольку угол падения светового потока на плоскость мал, а верхние – имеют большую освещенность в связи с большим углом падения, то средняя сферическая освещенность однозначно оценивает как боковые, так и верхние проемы. В этом заключается преимущество средней сферической освещенности. Эту характеристику лучше всего использовать при оценке условий освещения объемных объектов наблюдения, расположенных над плоскостью, что наблюдается в большинстве промышленных предприятий.
Средняя полусферическая освещенность (Е2 ) – средняя плотность светового потока на поверхности полусферы, радиус которой стремится к нулю. Эта величина является функцией точки и направления, т.е. при вращении полусферы значение освещенности будет меняться. Среднюю полусферическую освещенность лучше всего использовать при оценке условий освещения объемных объектов наблюдения с рельефной поверхностью, расположенных на плоскости.
Средняя цилиндрическая освещенность (Ец) – средняя плотность светового потока
на боковой поверхности вертикально расположенного цилиндра, диаметр которого и вы-
сота стремятся к нулю. Эта величина также является функцией точки и направления, т.к. при отклонении оси цилиндра от вертикального ее положения значение освещенности будет меняться. Среднюю цилиндрическую освещенность лучше всего использовать в тех помещениях, где зрительные операции осуществляются при горизонтальной линии зрения, а объекты наблюдения располагаются на вертикальной плоскости (выставочные павильоны, музеи, картинные галереи и т.п.). Следует отметить то, что средняя цилиндрическая освещенность для некоторых помещений нормируется в действующем в настоящее время СНиП ІІ-4-79.
Световой вектор определяет в любой точке поля модуль и направление вектора переноса световой энергии в единицу времени через единицу площади, перпендикулярной направлению переноса.
