
Начертательная геометрия
.pdf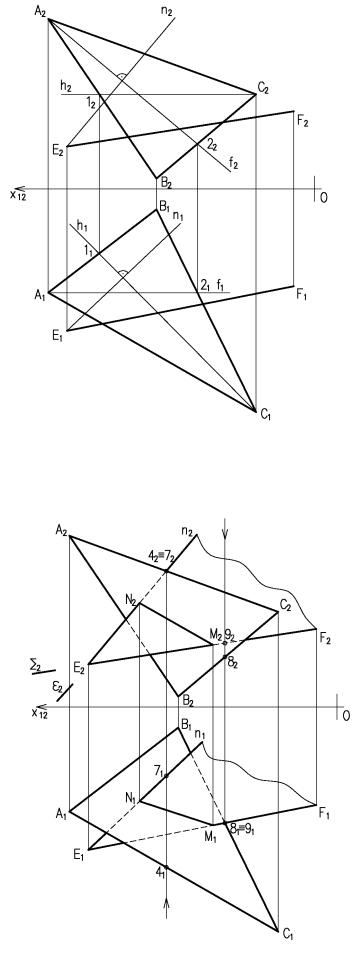
Две плоскости взаимно перпендикулярны, если одна из них содержит в себе перпендикуляр к другой плоскости. Поэтому наша задача заключается в том, чтобы из точки Е опустить перпендикуляр на пл.
∆АВС. Для этого воспользуемся следующим утверждением:
- прямая перпендикулярна плоскости, если она перпенди-
кулярна двум прямым, которые принадлежат этой плоскости
- в проекциях прямой угол
не изменяется только с прямыми,
которые параллельны плоскостям проекций, т.е. с горизонталью и фронталью.
Выходя из этого, проводим горизонталь h(h1;h2) и фронталь f(f1;f2) треугольника АВС. Затем из точки Е2 проводим прямую n2
перпендикулярно f2, а из точки Е1
прямую n1 перпендикулярно к h1.
Решение этого этапа даны на рисунке 5.
Плоскость β (ЕF × n )
перпендикулярна пл. ά (∆АВС).
Рисунок 5 – Построение линии пересечения (начало)
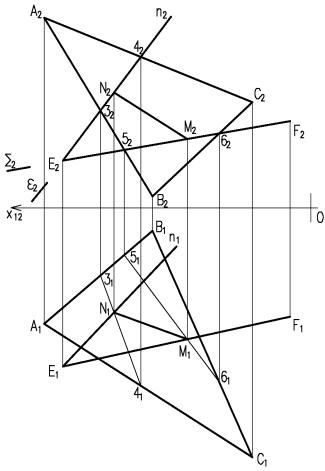
Рисунок 6 – Построение линии пересечения (продолжение)
20
|
Теперь приступим к постро- |
|
|||
ению линии пересечения этих |
|
||||
плоскостей. Для этого найдем |
|
||||
точки пересечения прямых n и ЕF |
|
||||
с плоскостью ά (∆АВС), соответ- |
|
||||
ственно т. N и M. Искомая ли- |
|
||||
ния - линия пересечения плоскостей- |
|
||||
будет проходить через эти две точки. |
|
||||
На |
рисунке |
6 |
выполнены |
|
|
построения |
|
|
|
||
по нахождению этой линии. |
|
||||
|
Для установления видимости |
|
|||
плоскостей на фронтальной проек- |
|
||||
ции возьмем на прямых АС и n пару |
|
||||
конкурирующих точек 4 и 7 (ри- |
Рисунок 7– Построение линии |
||||
сунок 7). На фронтальной проекции |
|||||
пересечения (окончание) |
|||||
т. 4 закрывает точку 7, т.к. у нее коор-
дината Y больше (см. на горизонтальные проекции этих точек), поэтому сторона АС видимая, а прямая n – невидимая.
Для установления видимости на горизонтальной проекции возьмем конкурирующие точки 8 и 9 на прямых ВС и ЕF, точка 8 имеет координату Z
большую (см. фронтальные проекции этих точек), т.е. она выше точки 9,
следовательно прямая ЕF – видимая, ВС – невидимая.
Задача 2.
Условие задачи 2 выбирается согласно варианта из таблицы 4. Следует начертить проекции произвольных размеров, сохраняя пропорции изображений.
21
Если треугольная пирамида пересекается плоскостью, то в общем случае (если плоскость не пересекает основание пирамиды) в сечении будет треугольник.
Для построения сечения необходимо найти точки пересечения ребер
АS, BC, CS в секущей плоскостью ά (m//n). Задачу определения точки пересечения прямой с плоскостью мы решали неоднократно.
Видимость ребер и прямых, которыми задана секущая плоскость определяется с помощью конкурирующих точек, см. задачу 2 на рисунке 8.
22

23
Рисунок 8 - Пример выполнения эпюра №1 (лист 3)
Таблица 3 - Варианты координат для выполнения задачи 1 графической
работы эпюр №1 (лист 3)
Вар/т |
|
A |
|
|
B |
|
|
C |
|
|
E |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коорд. |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
15 |
6 |
27 |
73 |
0 |
124 |
117 |
78 |
55 |
31 |
76 |
92 |
60 |
0 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
31 |
12 |
10 |
82 |
0 |
75 |
145 |
66 |
46 |
125 |
5 |
30 |
40 |
35 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
17 |
20 |
22 |
102 |
23 |
84 |
130 |
75 |
50 |
27 |
90 |
90 |
120 |
35 |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
50 |
28 |
22 |
143 |
60 |
100 |
95 |
80 |
13 |
47 |
90 |
73 |
135 |
45 |
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
12 |
107 |
14 |
88 |
125 |
64 |
68 |
0 |
25 |
108 |
120 |
0 |
35 |
30 |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
34 |
33 |
14 |
10 |
90 |
45 |
110 |
115 |
90 |
20 |
40 |
68 |
100 |
97 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
21 |
9 |
23 |
100 |
92 |
0 |
146 |
35 |
95 |
48 |
65 |
75 |
140 |
50 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
20 |
0 |
66 |
138 |
53 |
105 |
48 |
53 |
0 |
26 |
80 |
86 |
120 |
35 |
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
51 |
105 |
85 |
145 |
0 |
85 |
70 |
30 |
0 |
140 |
60 |
45 |
40 |
35 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
43 |
102 |
55 |
150 |
20 |
18 |
98 |
20 |
0 |
125 |
65 |
0 |
50 |
10 |
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
36 |
20 |
9 |
149 |
10 |
95 |
100 |
90 |
0 |
30 |
65 |
72 |
140 |
35 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
40 |
0 |
100 |
150 |
20 |
21 |
98 |
95 |
21 |
140 |
60 |
90 |
45 |
35 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
132 |
95 |
18 |
51 |
11 |
60 |
150 |
45 |
85 |
75 |
65 |
90 |
155 |
30 |
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
102 |
75 |
50 |
27 |
10 |
103 |
87 |
15 |
18 |
115 |
25 |
90 |
15 |
20 |
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
148 |
32 |
13 |
42 |
0 |
75 |
95 |
85 |
95 |
30 |
65 |
15 |
135 |
20 |
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
10 |
82 |
43 |
35 |
35 |
77 |
150 |
13 |
13 |
130 |
82 |
80 |
20 |
15 |
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
15 |
6 |
27 |
73 |
0 |
124 |
117 |
78 |
55 |
31 |
76 |
92 |
60 |
0 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
Продолжение таблицы 3
18 |
31 |
12 |
10 |
82 |
0 |
75 |
145 |
66 |
46 |
125 |
5 |
30 |
40 |
35 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
17 |
20 |
22 |
102 |
23 |
84 |
130 |
75 |
50 |
27 |
90 |
90 |
120 |
35 |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
50 |
28 |
22 |
143 |
60 |
100 |
95 |
80 |
13 |
47 |
90 |
73 |
135 |
45 |
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
12 |
107 |
14 |
88 |
125 |
64 |
68 |
0 |
25 |
108 |
120 |
0 |
35 |
30 |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
34 |
33 |
14 |
10 |
90 |
45 |
110 |
115 |
90 |
20 |
40 |
68 |
100 |
97 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
21 |
9 |
23 |
100 |
92 |
0 |
146 |
35 |
95 |
48 |
65 |
75 |
140 |
50 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
20 |
0 |
66 |
138 |
53 |
105 |
48 |
53 |
0 |
26 |
80 |
86 |
120 |
35 |
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
51 |
105 |
85 |
145 |
0 |
85 |
70 |
30 |
0 |
140 |
60 |
45 |
40 |
35 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
43 |
102 |
55 |
150 |
20 |
18 |
98 |
20 |
0 |
125 |
65 |
0 |
50 |
10 |
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
36 |
20 |
9 |
149 |
10 |
95 |
100 |
90 |
0 |
30 |
65 |
72 |
140 |
35 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
40 |
0 |
100 |
150 |
20 |
21 |
98 |
95 |
21 |
140 |
60 |
90 |
45 |
35 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
132 |
95 |
18 |
51 |
11 |
60 |
150 |
45 |
85 |
75 |
65 |
90 |
155 |
30 |
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
102 |
75 |
50 |
27 |
10 |
103 |
87 |
15 |
18 |
115 |
25 |
90 |
15 |
20 |
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25
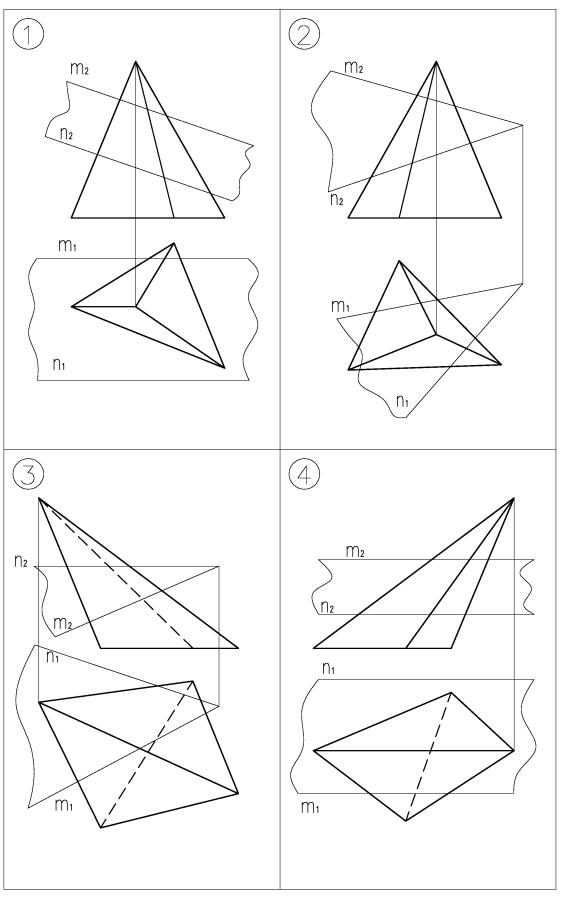
Таблица 4 - Варианты заданий для выполнения задачи 2 графической
работы эпюр №1 (лист 3)
26
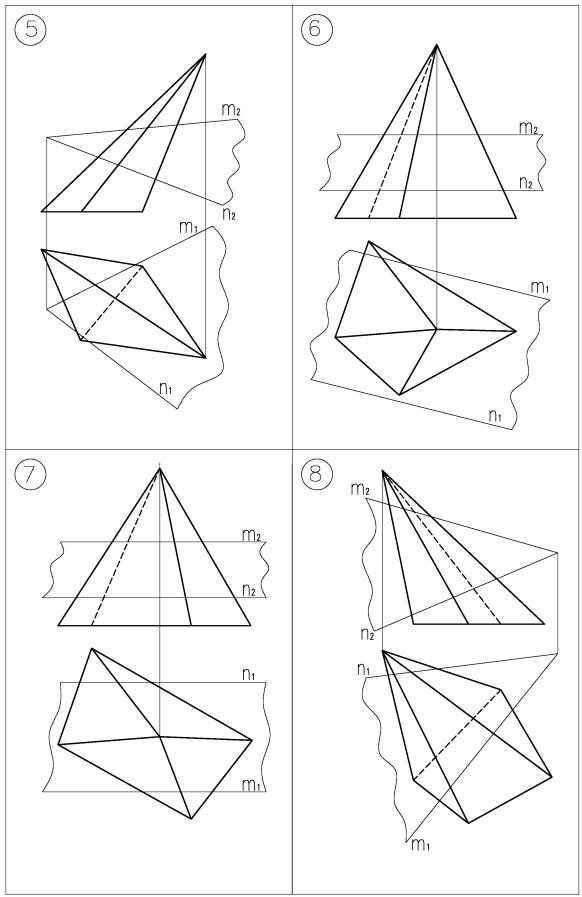
Продолжение таблицы 4
27
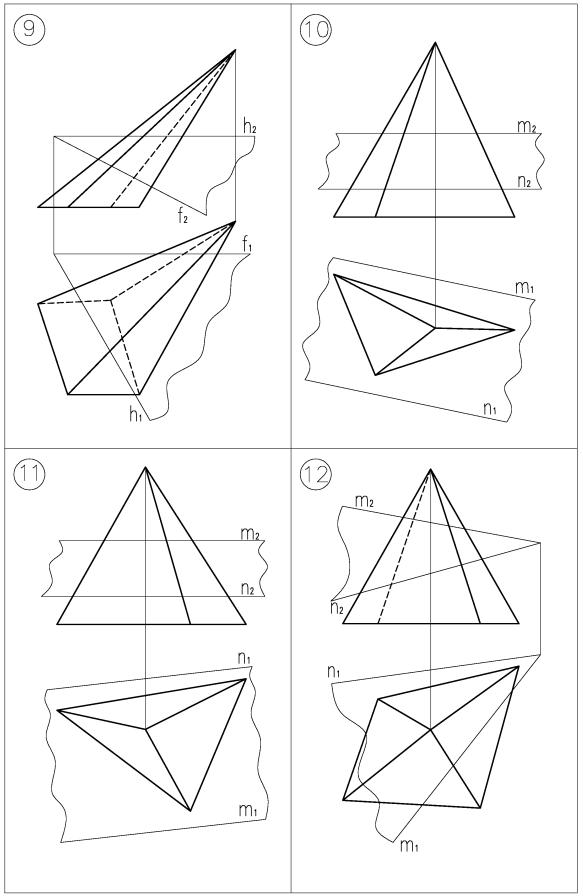
Продолжение таблицы 4
28
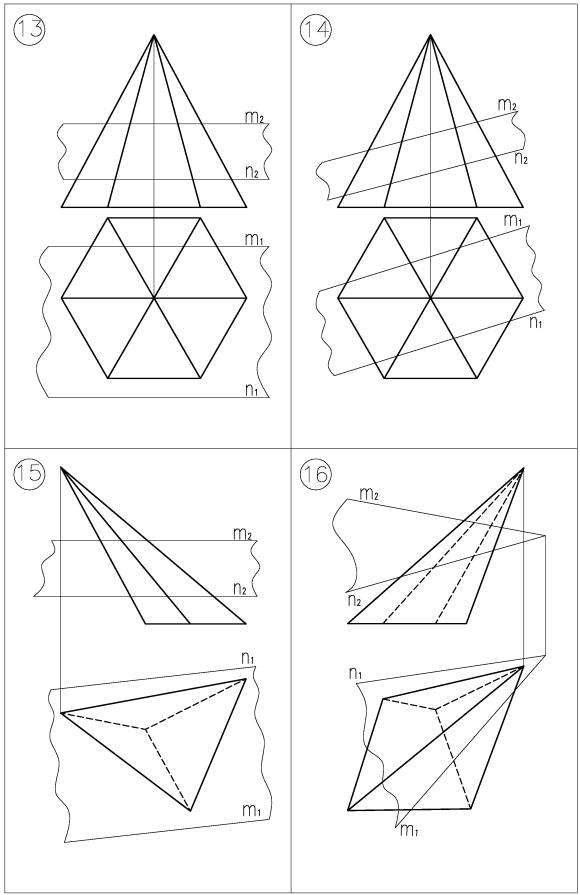
Продолжение таблицы 4
29
