konsp_lektsiy_1ch

31

В формуле (5.3) неизвестен закон распределения нормальных напряжений по площади поперечного сечения. Для ответа на этот вопрос на боковую поверхность элемента нанесем систему линий, перпендикулярных продольной оси элемента. После приложения нагрузки отмечаем, что эти линии не деформируются, а перемещаются поступательно. Это возможно в том случае, когда напряжения по площади поперечного сечения распределены равномерно.

Это предположение впервые высказал голландский ученый Д. Бернулли.

Гипотеза Бернулли – сечения плоские до деформации, остаются плоскими и после деформации.

Тогда, в случае равномерного распределения напряжений выражение (5.3) приобретает вид:

Nz z dF z F , откуда

F

Полученное выражение (5.4) совместно с условием прочности (5.2) дает возможность осуществить расчет на прочность. Так, например, пусть требуется определить площадь поперечного сечения для стержня на рис. 5.2, если он выполнен из стали с расчетным сопротивлением R=200МПа. На основании (5.4) и (5.2) запишем условие прочности

По длине стержня продольное усилие изменяется и принимает значения +2кН, -3кН и -6кН, что четко иллюстрирует эпюра продольных сил (рис. 5.2.б). Очевидно, что в последнее неравенство необходимо подставлять максимальное по модулю усилие Nz, тогда для всех остальных случает выполнение этого условия гарантировано. Максимальным по модулю в нашем случае является усилие Nz 6кН, которое и подставим в неравенство

Нужно заметить, что в связи с тем, что в расчетные формулы входят величины с различными производными единицами размерностей (МПа, см2, кН), рекомендуется при расчетах переводить все величины в систему СИ. Тогда конечный результат также будет иметь размерность единиц системы СИ.

Полученная величина площади позволяет подобрать сечение стержня. Например, для

Таким образом, для данного стержня подходит круглое сечение диаметром d=7мм.

Для определения деформаций рассмотрим стержень прямоугольного сечения длиной L с размерами поперечного сечения a и b. После приложения нагрузки стержень удлинился и длина его стала равной L1, а размеры поперечного сечения уменьшились и стали равными a1

и b1 (рис. 5.4).

32

На некотором расстоянии z выделим участок стержня длиной dz. После приложения нагрузки его длина станет равной dz+ dz. Относительная деформация, т.е. отношение величины деформации к первоначальной длине

dz , откуда dz

dz dz.

С учетом гипотезы Бернулли, если σ=const, следовательно, и ε=const, тогда получим:

l

L=ε dz =εL.

0

Продольная деформация при простом растяжении равна

Здесь L – абсолютная продольная деформация.

Рассуждая аналогично найдем поперечные деформации, которые берутся со знаком «-», так как сечение сужается:

Величины – a и b – абсолютные поперечные деформации. Для изотропных материалов

a b .

Французский ученый Пуассон установил, что отношение продольной деформации к поперечной есть величина постоянная, и равная коэффициенту Пуассона.

Коэффициент Пуассона μ меняется в пределах 0 0,5.

Многочисленные экспериментальные наблюдения за поведением деформируемых тел показывают, что в определенных диапазонах перемещения точек тела пропорциональны

33

действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Гуком и носит название закона Гука.

В соответствии с законом Гука перемещение произвольно взятой точки нагруженного тела по некоторому направлению, прямо пропорционально действующему в этом направлении усилию:

L kN.

Очевидно, что коэффициент k зависит от физико механических свойств материала, взаимного расположения расчетной точки и точки приложения и направления внешней нагрузки, а также от геометрических особенностей системы.

В современной трактовке закон Гука определяет линейную зависимость между напряжениями и деформациями, а не между силой и перемещением. Коэффициенты пропорциональности в этом случае представляют собой физико механические характеристики материала и уже не связаны с геометрическими особенностями системы в целом:

(5.7)

E ,

где Е – модуль упругости Юнга материала конструкции. Модуль упругости Юнга E является справочной величиной и характеризует упругие свойства материала конструкции. Измеряется модуль упругости в МПа, так же как и напряжения (5.4).

Формула (5.8) – закон Гука (5.7) для абсолютной деформации элемента.

EF – называют продольной жесткостью элемента или жесткостью при растяжении.

5.3. ПРИНЦИП СЕН-ВЕНАНА

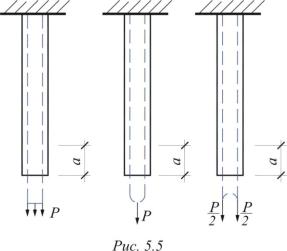
Формулы (5.4) и (5.8) получены для случая растяжения стержня распределенной нагрузкой, приложенной к его торцам. В том случае, когда нагрузка прикладывается другим способом (рис. 5.5), гипотеза Бернулли наблюдается только в тех сечениях, которые удалены от места приложения ее на расстояние, превышающее 1,5- 2 раза больший его поперечный размер.

Напряжения у мест приложения нагрузки распределены не равномерно, о чем свидетельствуют деформации у мест приложения нагрузки. Это явление по имени французского ученого называется принципом Сен-Венана.

Принцип Сен-Венана – при нагружении элемента статически эквивалентной нагрузкой, у которой главный вектор и главный момент системы сил одинаковы, в сечениях, достаточно удаленных от мест приложения нагрузки, напряжения мало зависят от способа приложения нагрузки.

34

5.4. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ ПРИ РАСТЯЖЕНИИ

Испытание на растяжение является основным видом исследования при определении механических свойств материала. Испытания производят на специальных машинах, создающих растягивающую нагрузку. Для испытания берут стандартные образцы: l0 = 10d0. Замеряют l0, d0 до испытания и l1, d1 после испытания Эскиз образца до испытания “а” и после испытания “б” представлен на рис. 5.6.

Рис.5.6.

В процессе испытаний на диаграммном аппарате разрывной машины автоматически записывается зависимость деформаций образца ∆li от величины действующей нагрузки Pi (рис. 5.7. Диаграмма растяжения стали).

Рис.5.7. Диаграмма растяжения стали

Характерными точками диаграммы являются:

А – соответствует наибольшей нагрузки Рпц, при которой соблюдается линейная зависимость между напряжениями и деформациями. На этом участке справедлив закон Гука σ = Е .

В – соответствует наибольшей нагрузке Рупр., при которой материал образца сохраняет упругие свойства.

CD – площадка текучести. Соответствует нагрузке Рт, при которой деформации растут без увеличения нагрузки.

Е – соответствует максимальной нагрузке, которую может выдержать образец Рвр. G – соответствует нагрузке Рразр, при которой происходит разрыв образца.

35

Используя указанные величины Рпц, Рупр., Рт, Рв, полученные в процессе испытаний, определяют характеристики прочности материала: σпц, σупр., σт, σв.

равен Е – модулю упругости I-рода (рис.5.7).

tgα = E = 2,1 105 МПа.

Вертикаль, проведенная через точку В диаграммы растяжения, делит её на две части: левая часть – зона упругих деформаций; правая часть – зона упругопластических деформаций (рис.5.7)

36

ЛЕКЦИЯ № 6. ПОПЕРЕЧНЫЙ ИЗГИБ БРУСА. ВНУТРЕННИЕ УСИЛИЯ, ПОНЯТИЕ ЧИСТОГО ИЗГИБА. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ ПРИ ПЛОСКОМ ИЗГИБЕ В БАЛКАХ.

6.1. ПОПЕРЕЧНЫЙ ИЗГИБ БРУСА

Одной из распространенных деформаций конструкций является изгиб. Изгибу подвержены стволы деревьев при действии ветровой нагрузки, балки мостов, перекрытий и пр. Такой вид деформации появляется при действии на брус поперечных сил и характеризуется изменением кривизны бруса. В том случае, когда все силы, действующие на брус, располагаются в плоскостях, проходящих через продольную ось стержня, изгиб называется поперечным.

Поперечный изгиб – такой вид деформации, при котором действующая нагрузка расположена в плоскостях, совпадающих с продольной осью стержня (рис. 6.1).

В том случае, когда действующая нагрузка расположена в одной плоскости, проходящей через одну из главных осей поперечного сечения, изгиб называется плоским поперечным или просто плоским.

Таким образом, плоский изгиб является частным случаем поперечного изгиба.

Изгиб стержня в вертикальной плоскости относительно главной центральной оси чаще всего называют просто изгибом. Стержни, подверженные деформации изгиба, называются балками.

Балки прикрепляются к неподвижным основаниям при помощи опорных устройств – внешних связей, среди которых выделяют четыре основных: шарнирно-подвижная опора, шарнирно-неподвижная опора, жесткая заделка и ползун.

Для расчета балки необходимо знать всю внешнюю нагрузку как активные силы так и реактивные силы. Поскольку опорные реакции чаще всего не задаются, то расчет балки нужно начинать с вычисления опорных реакций. Для этого используют условия равновесия тела. Для системы сил на плоскости могут быть составлены лишь три независимых уравнения равновесия тела. При этом для контроля правильности вычислений рекомендуется определение опорных реакций балок производить по следующему алгоритму.

Алгоритм определения реакций в балке:

37

1.ΣFz = 0 → Ha

2.ΣMa = 0 → Rb

3.ΣMb = 0 → Ra

4.Требуется доказать ΣFy = 0.

Проиллюстрируем действие алгоритма определения опорных реакций в балке на следующем примере.

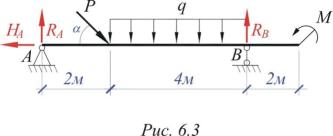
Пример 6.1. Определить опорные реакции балки при заданных значениях нагрузки

(рис. 6.3): q= 5 кН/м, Р = 20 кН, М=10 кНм, =450.

В точке А балка имеет внешнюю связь (1.14) в виде шарнирно-неподвижной опоры (2.4). В соответствии с аксиомой освобождаемости от связей (1.22) данную связь можно заменить силами реакций НА и RА. В точке В балка имеет внешнюю связь (1.14) в виде шарнирно-подвижной опоры (2.3). Аналогично данную связь

можно заменить силой реакции RВ. Определение реакций ведем в соответствии с алгоритмом определения опорных реакций в балке (6.4):

1.ΣFz = 0, Pcos -Ha = 0, → Ha= Pcos =20 0,707=14,14 (кН)

2.ΣMА = 0, -Psin 2-q 4 (2+2)+RB 6+M=0, →

4. Проверка: ΣFy = RB + RA –Psin –q 4=16,38+17,76 – 20 0,707 – 5 4=31,14 – 31,14 0.

Реакции определены верно.

6.2. ВНУТРЕННИЕ УСИЛИЯ, ПОНЯТИЕ ЧИСТОГО ИЗГИБА

Внутренние усилия в балке определяются при плоском поперечном изгибе общим методом сечений. Для этого балка разрезается поперечным сечением и рассматривается одна из отсеченных частей в равновесии под действием внешних и внутренних сил, приложенных к отсеченной части. На рис. 6.4 показана балка, загруженная сосредоточенной силой Р. Разрежем ее поперечным сечением m-m на некотором расстоянии z от левой опоры. Внешняя нагрузка на балку, представленная реакцией RA, может быть уравновешена потоком касательных усилий, направленных вниз. Равнодействующая потока касательных усилий в сечении называется поперечной силой.

Из условия равновесия получим: Fy 0, Qy RA .

Однако только поперечной силой Qy обеспечить равновесие левой части балки нельзя, поскольку поперечная сила Qy и реакция RA составляют пару силу, момент которой составит

RA z.

Для обеспечения равновесия в поперечном сечении появляются нормальные (перпендикулярные к плоскости сечения) усилия. Очевидно, что нормальные усилия должны

быть уравновешены, поскольку Fx 0, т.е. одна их часть направлена вправо, другая влево.

38

При этом, не рассматривая закон распределения этих усилий по площади сечения, можно заметить, что они образуют момент равный по величине и противоположный по направлению моменту, образованного силами Qy и RA. Момент внутренних нормальных усилий в сечении балки называется изгибающим моментом.

Из условия равновесия балки получим Mx RA z .

Аналогично рассмотрим правую часть балки. Из условия равновесия правой части балки следует, что поток касательных усилий в рассматриваемом сечении направлен вверх. Обозначив его также Qy, найдем, что Qy= P-RB.

Поскольку P- RB= RA, то получаем, что Qy – это та же самая поперечная сила, которая была приложена к левой части балки вниз, но теперь она приложена к правой части балки вверх.

Таким образом, направление поперечной силы зависит от того, какая из отсеченных частей в данный момент рассматривается. Если балку не разрезать, то нельзя ставить вопрос об изображение поперечной силы, поскольку поперечная сила является внутренней силой, которую можно показать только в месте разреза. Действительно, сложив две части балки, получим целую балку, и поперечные силы при этом будут уравновешены. Поэтому на расчетной схеме балки (не разрезанной) поперечные силы не показываются, а есть только внешняя нагрузка.

Таким же образом из условий равновесия правой части балки находим изгибающий момент:

Mx=RB(a+b-z)-P(a-z).

Подставив сюда значение реакции RB=P-RA, получим значение

Mx=P(a-z+b)-RА(a+b-z)-P(a-z)=[P b-RА(a+b)]+ RА z= RА z.

(Здесь выражение в квадратных скобках представляет собой момент всех внешних сил относительно точки B, который из условия равновесия равен нулю.)

Таким образом, поперечная сила равна сумме проекций всех внешних сил, расположенных по одну сторону от сечения, на направление перпендикулярное продольной оси стержня, и взятых с определенным знаком. Необходимо отметить, что при вычислении поперечной силы, нагрузка, направленная вверх слева от сечения, принимается положительной, а при рассмотрении правой части балки отрицательной. С помощью метода

39

сечений эти знаки получаются автоматически. Однако на практике при вычислении внутренних силовых факторов все этапы метода сечений, как правило, выполнять нет необходимости, просто учитывается вся нагрузка с одной стороны от сечения. При этом нужно строго придерживаться правила знаков. Положительные направления поперечных сил при различных расположениях сечения представлены на рис. 6.5а.

Изгибающий момент равен сумме моментов всех внешних нагрузок (сил и пар сил), расположенных по одну сторону от сечения и взятых с определенным знаком.

Изгибающий момент считается положительным, если он вызывает растяжение нижних волокон балки. Положительные направления изгибающих моментов при различных расположениях сечения представлены на рис. 6.5б.

Использование правила знаков (рис. 6.5) при определении внутренних силовых факторов в некотором сечении m-m, позволяет сразу (без записи уравнений равновесия) составить выражение суммы проекций сил или суммы моментов сил, расположенных на отсеченной части балки, с учетом их знака. Для этого при рассмотрении левой отсеченной части положительными считают направления поперечных сил и моментов, расположенных по левую сторону от сечения m-m правила знаков. При рассмотрении правой отсеченной части положительными считают направления поперечных сил и моментов, расположенных по правую сторону от сечения m-m правила знаков.

В случае, когда в поперечном сечении балки действует только изгибающий момент, а поперечная сила равна нулю, изгиб называется чистым.

6.3. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ

Рассмотрим некоторую консольную балку (рис. 6.6), к которой приложена нагрузка, изменяющаяся по произвольному закону. Вырежем из балки бесконечно малый элемент длиной dz, в пределах которого распределенную нагрузку можно считать равномерно распределенной.

На левой и правой грани рассматриваемого элемента действуют положительные внутренние силовые факторы. Под действием приложенной нагрузки и внутренних силовых факторов выделенный элемент должен находиться в равновесии. Запишем уравнения статики:

40

Знак «+» или «-» в формулах (6.1) и (6.2) зависят от направления оси z. Для правосторонней системы координат берется знак «+».

Первая зависимость (6.1) называется первой теоремой Журавского, вторая (6.2) – второй теоремой Журавского.

6.4. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ ПРИ ПЛОСКОМ ИЗГИБЕ В БАЛКАХ

Внутренние силовые факторы изменяются в зависимости от положения сечения. Характер изменения изгибающего момента и поперечной силы по длине балки представляют в виде эпюр.

Построение эпюр внутренних силовых факторов в балках выполняется в определенной последовательности.

1.Вычисляется и показывается на расчетной схеме вся внешняя нагрузка. Обычно активная нагрузка задается, а реакции опор следует определить.

2.Балка разбивается на отдельные участки. Участком балки называют часть балки между точками приложения сосредоточенных нагрузок, точками начала или окончания распределенной нагрузки.

3.На каждом участке вводится "плавающая" система координат, нуль которой совмещается с одной из границ участка балки и составляются аналитические выражения для изгибающего момента и поперечной силы.

4.По аналитическим функциям внутренних силовых факторов и их значениям на границах участков балки строятся эпюры. При этом на эпюре Qy положительная ордината откладывается вверх, а на эпюре Mx вниз. Это связано с принятым правилом знаков. Принято говорить, что эпюра Mx строится со стороны растянутого волокна балки.

5.Дифференциальные зависимости (6.1) и (6.2) используются для контроля правильности построения эпюр.

6.

Пример 6.2. Построить эпюры изгибающих моментов и поперечных сил для заданной балки (рис. 6.7).

1) Определяем опорные реакции

(см. пример 6.1): RA=17.76кН, HA=0, RB=16.38кН.

2) Разбиваем балку на участки: балка содержит 3 участка – АС, СВ и BD.

3) На участках АС и СВ в произвольном месте проводим сечение соответственно I-I и II-II и рассматриваем левую отсеченную часть балки. Для этого на каждом участке вводим систему координат z1 и z2, совмещая её начало с левой границей участка. На участке ВD проводим сечение III-III и рассматриваем отсеченную правую часть. Нуль системы координат z3 совмещаем с правой границей участка.