konsp_lektsiy_1ch

41

ЗАМЕЧАНИЕ 1. Каждый участок рассматривается независимо от других. Так, рассматривая, например, участок 2 рассеченный сечением II-II, все остальные сечения игнорируют. Т.е. каждое сечение разрезает балку только на две части – правую и левую.

ЗАМЕЧАНИЕ 2. Начало местной системы координат zi на участке совмещается с одной из границ участка балки (6.8). При этом, если рассматривается левая отсеченная часть, то начало координат совмещается с левой границей участка, при рассмотрении правой отсеченной части – с правой границей. Выбор между левой и правой частью осуществляется произвольно, как правило, по принципу наименьшей сложности анализа.

Составляем аналитические зависимости:

Участок 1 0≤z1≤2м.

Qy=RA=17.76 кН.

Получили постоянное значение, не зависящее от координаты z1.

Mx= RA z1=17.76 z1.

Получили прямолинейную зависимость момента Mx от координаты z1. Для построения этой прямой достаточно знать значение функции в 2-ух точках.

Mx(0)=17.76 0=0.

Mx(2)= 17.76 2= 35.52 кНм.

Получили квадратичную зависимость момента Mx от координаты z2. Для построения этой квадратной параболы определим значения функции на границах участка.

Mx(0)=35.52+3.62 0 – 2.5 02=35.52 кНм. Mx(4)= 35.52+3.62 4 – 2.5 42=10 кНм.

Для построения параболы выясним местоположение её вершины. Известно, что положение экстремума любой функции может быть найдено путем приравнивания первой производно к нулю:

участок Найдем значение момента в вершине параболы:

Mx,max = Mx(0.724)= 35.52+3.62 0.724 – 2.5 0.7242=36.83 кНм.

Определим направление выпуклости параболы. Для этого воспользуемся анализом второй производной функции по координате:

Однако, поскольку на эпюре моментов положительные ординаты откладывают снизу, то парабола имеет выпуклость вниз. Для уменьшения путаницы, связанной с системой

42

координат, при построении эпюры моментов, говорят, что парабола на эпюре моментов выпукла в направлении распределенной нагрузки на участке.

ЗАМЕЧАНИЕ 3. В том случае, когда вершина параболы не попадает на рассматриваемый участок, парабола может быть построена по граничным значениям и направлению выпуклости.

Участок 3 0≤z3≤2м.

Qy=0.

Mx= M=10кНм.

Очевидно, что последний участок балки является участком чистого изгиба .

4)По полученным аналитически точкам строим эпюры Mx и Qy (рис. 6.7). При этом на эпюре Qy положительная ордината откладывается вверх, а на эпюре Mx вниз. Значения ординат проставляются в начале и в конце каждого участка, а также в экстремальных точках

суказанием их местоположения. Знаки ординат указывают на эпюре в кружке. Эпюры подписывают и проставляют размерности ординат.

5)Контроль правильности построенных эпюр начинают обычно с проверки скачков.

Скачком называется разрыв функции второго рода, когда lim f (z) lim f (z). Такие скачки

z a 0 z a 0

появляются на эпюре поперечных сил в точках, где приложены на балке сосредоточенные силы, а на эпюре моментов в точках, где приложены сосредоточенные моменты. При этом, величина скачка должна быть равна величине сосредоточенной нагрузки в данной точке. Так, для нашего примера имеем скачки на эпюре Qy в точках А, С и В, которые соответственно равны – 17.76кН, 14.14 кН и 16.38кН. Скачки соответствуют приложенным в этих точках сосредоточенным нагрузкам. На эпюре моментов Mx скачок присутствует только в точке D, равный 10кНм, что соответствует приложенному в этой точке сосредоточенному моменту М=10кНм.

ЗАМЕЧАНИЕ 4. При отсутствии в точке сосредоточенной нагрузки никаких скачков на эпюрах балки быть не должно.

Также в качестве проверки используют следствие дифференциальных зависимостей (6.1) и (6.2). Так, при q=0, получим, что Qy =const, а Mx=f(z), т.е. на участке, где распределенная нагрузка отсутствует, поперечная сила постоянна и эпюра имеет вид горизонтальной линии, а эпюра моментов имеет вид произвольной прямой. Такими участками на балке являются участок 1 и 3. При q=const, получим, что Qy = f(z), а Mx=f(z2), т.е. на участке, где есть равномерно распределенная нагрузка, поперечная сила имеет вид произвольной прямой, а эпюра моментов имеет вид квадратной параболы. Таким участком на балке является участок 2.

ЛЕКЦИЯ № 7. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ. РАЦИОНАЛЬНОЕ СЕЧЕНИЕ БАЛОК. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ ИЗГИБЕ

7.1. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ

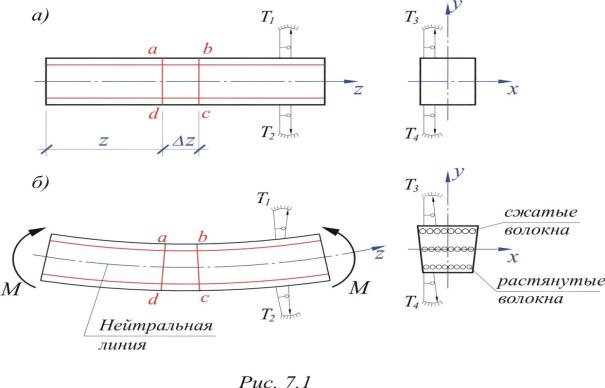
Поскольку изгибающий момент является моментом внутренних нормальных усилий в поперечном сечении, то для определения нормальных напряжений рассмотрим стержень в состоянии чистого изгиба, когда в сечениях возникают только изгибающие моменты. Это может быть балка, загруженная по торцам моментами (рис. 7.1). Задача определения

43

нормальных напряжений является статически неопределимой, так как не известен закон распределения нормальных напряжений по высоте сечения балки. Поэтому необходимы дополнительные условия, которые можно получить исходя из экспериментальной практики наблюдения за деформациями балки при чистом изгибе.

Для начала рассмотрим балку, имеющую ось симметрии в плоскости изгиба, например, балку прямоугольного сечения (рис. 7.1). На боковой поверхности балки нанесем продольные и поперечные линии (на рис. 7.1 по две таких линии). На нижней и верхней поверхности установим четыре тензометра, которые ориентируем попарно вдоль балки и поперек балки (рис. 7.1.а). (Тензометр – прибор рычажного типа, позволяющий измерить изменение расстояния между двумя точками.)

После загружения продольные линии искривляются и изменяются по длине. Верхние линии (a-b) становятся короче, а нижние (c-d) длиннее, о чем свидетельствует показания тензометров Т1 и Т2. При переходе от растяжения к сжатию можно выделить линии, длина которых не изменяется. Назовем такие линии нейтральными. Поперечные линии не искривляются, а лишь поворачиваются вокруг некоторых точек, лежащих на нейтральной линии.

В поперечном сечении торцы балки деформируются, сохраняя ось симметрии. Вверху балка становится шире, а внизу – уже, о чем свидетельствуют показания тензометров Т3 и Т4. Деформации продольные (по тензометрам Т1, Т2) в несколько раз превышают поперечные, и связь между ними такая же, как и при растяжении через коэффициент Пуассона.

На основании экспериментальных наблюдений вводятся некоторые гипотезы.

Гипотеза плоских сечений (гипотеза Бернулли). Сечения, плоские до загружения балки, остаются плоскими и после загружения, поворачиваясь вокруг некоторой линии.

Гипотеза о не надавливании волокон друг на друга. Волокна балки при чистом изгибе не давят друг на друга, а находятся в состоянии простого растяжения.

Волокна понятие условное, представляющее собой некоторую нить предельно малой толщины, параллельную продольной оси балки. Представим, что балка изготовлена из отдельных склеенных между собой проволок. После загружения верхние проволоки, испытывающие сжатие, становятся толще, но они не нажимают друг на друга, а просто балка

44

в этом месте становится шире. Нижние проволоки растягиваются и становятся тоньше, не отрываясь друг от друга, просто сечение в этом месте становится уже. Есть также волокна, которые не претерпевают удлинений, которые называют нейтральными. Нейтральные волокна формируют нейтральный слой.

Нейтральным слоем называют слой, который при деформации не изменяет своей длины. Нейтральной линией называется линия пересечения нейтрального слоя с поперечным сечением.

Деформация балки изменяется по высоте сечения, а по ширине остается постоянной. Следствием этого является сохранение оси симметрии при загружении. После загружения поперечные сечения имеют вид равнобокой трапеции.

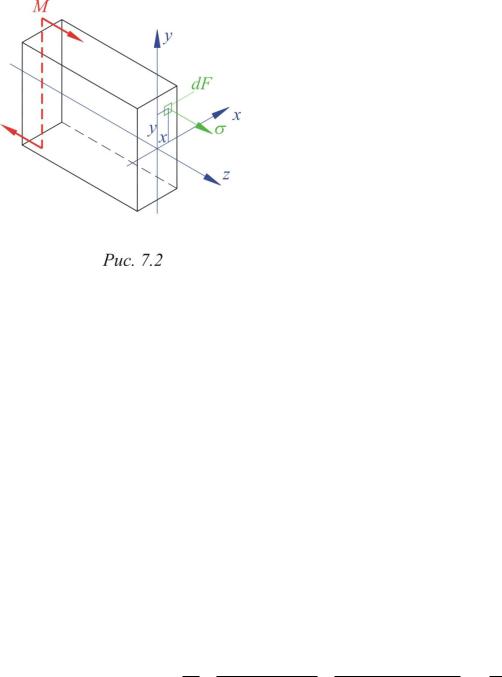
Разрежем балку на две части и рассмотрим одну из них в равновесии под действием внешних и внутренних сил (рис. 7.2).

Выберем систему координат:

z – продольная ось балки; y – ось симметрии, совпадающая с плоскостью загружения; х – нейтральная ось, положение которой пока не известно. Пусть в некоторой точке с координатами (x,y) расположена бесконечно малая площадка dF с напряжением . Система сил, приложенных к элементу, объемная. Из шести уравнений три тождественно равны нулю. Остальные три уравнения можно записать в виде:

Mx 0, dF y M , поскольку в данном случае Мx M , то

F

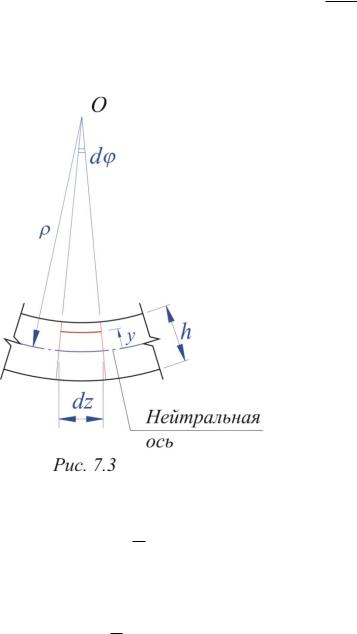
Для вычисления этих интегралов необходимо знать распределение напряжений по площади F. Для получения такого распределения вырежем на расстоянии z двумя сечениями, расположенными на расстоянии dz, элемент балки и рассмотрим его в деформированном состоянии (рис. 7.3). Нас интересует деформация волокна, взятого на произвольном расстоянии y от нейтральной оси. Первоначальная длина этого волокна, как и всех других, была равна dz. После деформации такая длина сохранилась лишь на нейтральной оси балки. При dz 0 будем полагать, что рассматриваемая часть балки искривляется по некоторой окружности с радиусом . Радиус будем называть радиусом кривизны изогнутой балки. По рис. 7.3 очевидно, что dz= d . Длина рассматриваемого волокна будет составит ( -y) d . Относительная деформация волокна

l ( y)d dz ( y)d d y . l dz d

Согласно второй гипотезе на основании закона Гука получим

46

Из формулы (7.6) очевидно, что нормальные напряжения по высоте сечения изменяются по линейному закон у. Максимальная величина напряжений возникает в наиболее удаленных волокнах от нейтральной оси:

Здесь Wх – момент сопротивления площади относительно оси х.

7.2. РАЦИОНАЛЬНОЕ СЕЧЕНИЕ БАЛОК

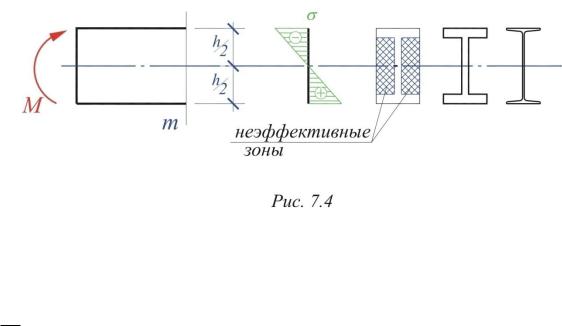
На рис. (7.4) показана эпюра распределения нормальных напряжений по высоте сечения балки. Учитывая, что напряжения по высоте сечения балки распределены не равномерно, материал, расположенный возле нейтрального слоя нагружен мало. Поэтому в целях экономии и снижения веса конструкции для элементов, работающих на изгиб, следует выбирать такую форму поперечного сечения, чтобы большая часть материала была удалена от нейтральной линии. Если из прямоугольного сечения удалить материал в непосредственной близости к нейтральной линии, то получим двутавровый профиль.

В соответствии с (7.6) геометрической характеристикой, которая регламентирует несущую способность балки при изгибе, является момент сопротивления Wx. Масса балки пропорциональна площади поперечного сечения F. Следовательно, чем больше величина этого соотношения момента сопротивления к площади сечения, тем более балка эффективна.

Wx - критерий оценки эффективности профиля.

F

7.3. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ

При поперечном изгибе бруса в сечениях балки действуют изгибающие моменты и поперечные силы. Изгибающие моменты вызывают действие нормальных напряжений, поперечные (перерезывающие) силы – касательные напряжения. Касательные напряжения возникают не только в поперечных, но и в продольных сечениях. При этом происходит сдвиг волокон относительно друг друга, что противоречит гипотезе плоских сечений. Однако, как сказано выше, влияние этого фактора на величину нормальных напряжений не велико.

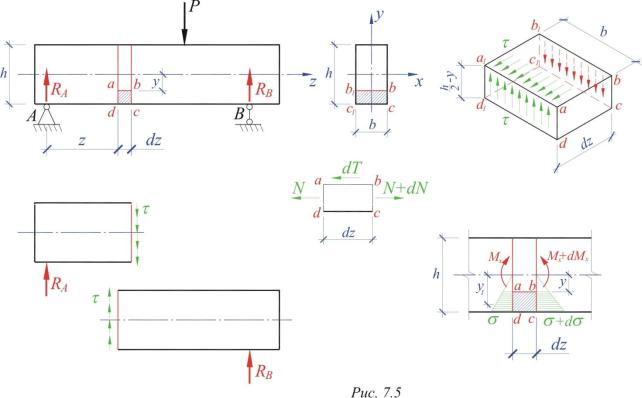
Рассмотрим балку прямоугольного поперечного сечения, загруженную сосредоточенной силой Р (рис. 7.5). Вырежем двумя поперечными сечениями на расстоянии dz друг от друга элемент балки. По граням этого элемента действуют касательные напряжения, направленные в разные стороны. Из этого элемента горизонтальной плоскостью на произвольном расстоянии y от нейтральной оси отрезаем параллелепипед и рассмотрим его в равновесии.

47

Введем гипотезу о распределении касательных напряжений по ширине сечения балки. Касательные напряжения в балке, на некотором расстоянии у от нейтральной оси, по ширине сечения постоянны и направлены в сторону действия поперечной силы.

Эти напряжения легко определяются из уравнения равновесия параллелепипеда:

dT=dN.

Здесь dT = b dz – равнодействующая касательных усилий на горизонтальной грани аbb1a1.

Равнодействующая нормальных усилий на левой вертикальной грани аdd1a1:

Здесь Sxотс - статический момент площади отсеченной части (грани аdd1a1) относительно

нейтральной оси х.

Аналогично можно найти равнодействующую нормальных усилий N+dN на правой грани параллелепипеда, где в отличие от левой грани действует изгибающий момент Mx+dMx. Следовательно,

получим расчетную формулу для определения касательных напряжений при изгибе:

48

В формуле (7.7) обозначено:

τ- касательные напряжения в поперечном сечении балки на расстоянии у от нейтрального слоя;

Qy – поперечная сила в сечении балки, в котором вычисляются касательные напряжения;

Sxотс – статический момент площади отсеченной части поперечного сечения, расположенного выше или ниже уровня у, относительно нейтральной оси х;

b – ширина сечения балки в том месте по высоте сечения, где определяются касательные напряжения,

Ix – осевой момент инерции площади всего поперечного сечения относительно оси х.

Формула (7.7) получена русским ученым Журавским и носит его имя.

7.4. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ ИЗГИБЕ НА ПРИМЕРЕ БАЛКИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ

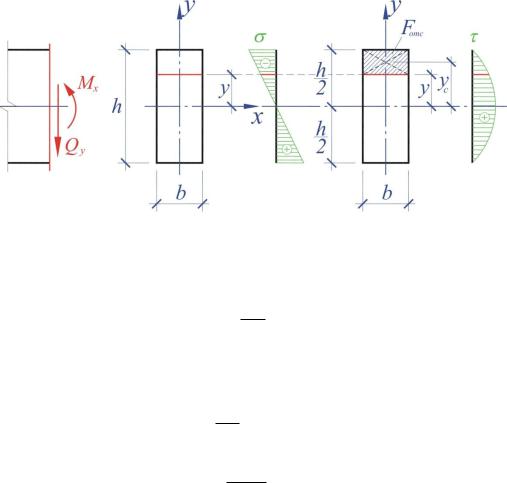
Рассмотрим балку прямоугольного поперечного сечения с размерами b и h (рис. 7.6). В произвольном сечении балки действует изгибающий момент Мх и поперечная сила Qy. Определим нормальные и касательные напряжения на уровне у от нейтральной оси х.

Рис. 7.6.

Нормальные напряжения определяем по формуле (7.6):

Mx y .

Ix

Момент инерции прямоугольного поперечного сечения:

bh3

Ix 12 , тогда

12Mx y. bh3

49

Очевидно, что нормальные напряжения линейно зависят от координаты y в сечении. Максимальные нормальные напряжения возникают в точках наиболее удаленных от нейтральной оси x и составляют:

max 6M2x .

bh

Эпюра распределения нормальных напряжений в сечении приведена на рис. 7.6. Касательные напряжения определяем по формуле (7.7):

Qy Sxотс .

Ixb

Статический момент площади отсеченной части поперечного сечения, лежащей выше уровня у, можно определить как

Из полученной зависимости следует, что касательные напряжения по высоте сечения балки изменяются по параболическому закону.

Эпюра распределения касательных напряжений в сечении приведена на рис. 7.6.

Анализируя эпюры касательных и нормальных напряжений, можно сделать вывод о том, что в точках максимальных нормальных напряжений касательные равны нулю, и, наоборот, в точках максимальных касательных напряжений нулю равны нормальные. В

этих точках условие прочности может быть записано в виде:

Здесь Rср – расчетные сопротивления срезу.

Как было показано ранее, условие прочности заключается в сравнении величины

действующих напряжений с максимально допустимой величиной – расчетным сопротивлением. Однако в нашем случае существуют точки, в которых действует не одно, а два напряжения различного направления. В этом случае для расчетов на прочность

50

используются так называемые теории прочности. Полное изучение теорий прочности выходит за рамки настоящего курса, поэтому остановимся лишь на расчетных формулах, применяющихся при расчетах металлических и бетонных конструкций. Расчетные напряжения по третьей теории прочности определяются как:

σIIIр 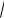σ2 4τ2 R .

Третья теория хорошо согласуется с опытными данными по испытанию материалов как хрупких, так и пластичных, одинаково работающих на растяжение и сжатие.

Расчетные напряжения по четвертой теории прочности определяются как

σIVр σ2 3τ2 R.

Четвертая теория применяется обычно для материалов пластичных и положена в основу современных норм расчета стальных конструкций.