
konsp_lektsiy_1ch
.pdf
21
С помощью этой аксиомы устанавливается, в частности, связь между условиями равновесия сил, приложенных к абсолютно твердому телу и деформируемому телу. Из аксиомы следует, что условия равновесия сил, приложенных к абсолютно твердому телу, необходимы и для равновесия деформируемого тела.
Аксиома освобождаемости от связей: состояние тела не изменится, если отбросить |
|
||||||||
какие-либо из наложенных связей, заменив их действие силами реакций. |
|
|
|
||||||
à) |
|
á) |
|
Пусть некоторое тело находится в состоянии |
|||||
F1 |
F2 |
F1 |
|
равновесия |
и |
имеет внешнюю |
связь в |
точке |
K |
RK |
F2 (рис. 3.9.а). |
Тогда, в соответствии с |
аксиомой |
||||||
|
|
|
освобождаемости от связей, тело может быть |
||||||
K |
|
|
K |
представлено освобожденным от связи, но с |
|||||
|
|
приложением |
дополнительной |
внешней |
силы |
– |
|||
|
Рис.3.9. |
|
реакции RK |
в точке K (рис. 3.9.б). |
|
|
|
||
Величина реакции в этом случае определяется из условия равновесия исходного тела. Направление силы реакции связи принимается совпадающим с направлением запрещенного перемещения точки K тела в месте наложения внешней связи.
ЛЕКЦИЯ № 4. ВИДЫ СВЯЗЕЙ И РЕАКЦИИ СВЯЗЕЙ. ПОНЯТИЕ МОМЕНТА СИЛЫ, МОМЕНТ ПАРЫ СИЛ. УСЛОВИЕ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ. СИСТЕМА СХОДЯЩИХСЯ И ПАРАЛЛЕЛЬНЫХ СИЛ.
4.1.ВИДЫ СВЯЗЕЙ И РЕАКЦИИ СВЯЗЕЙ
Вокружающем нас реальном мире в пределах поверхности земли все твердые тела являются трехмерными, т.е. они имеют три линейных независимых друг от друга измерения.
Вевклидовой геометрии независимость линейных измерений обеспечивается их взаимным перпендикулярным друг к другу направлением, т.е. иначе: осями декартовой системы координат.
Каждое абсолютно твердое тело состоит из континуума материальных точек, представляющих собой неизменную совокупность. Перемещение тела в пространстве может быть выполнено тремя одновременными прямолинейными перемещениями всех его точек вдоль координатных осей и тремя независимыми вращениями всего тела вокруг каждой из них.
Вмеханике каждое независимое перемещение абсолютно твердого тела называется его степенью свободы.
Свободное абсолютно твердое тело в пространстве имеет шесть степеней свободы: три прямолинейных перемещения вдоль трех взаимно перпендикулярных направлений и три поворота (по одному вокруг каждого из этих направлений). Если абсолютно твердое тело движется так, что все его точки перемещаются в параллельных плоскостях, то можно рассматривать перемещение одного из его характерных сечений в плоскости, совпадающей с плоскостью самого сечения тела. В этом случае перемещение тела называется плоским, при котором оно имеет три независимых перемещения, т.е. три степени свободы (1.2): два линейных перемещения вдоль двух взаимно перпендикулярных направлений, лежащих в плоскости сечения, и один поворот сечения тела вокруг любой точки, которая лежит в плоскости сечения.
Таким образом, свободное абсолютно твердое тело при перемещении в пространстве имеет шесть степеней свободы, а при перемещении в плоскости – три степени свободы.
Тем не менее, при решении задач, связанных с расчетом и анализом сооружений, практически всегда приходится иметь дело с рассмотрением несвободных абсолютно
22
твердых тел. В своем естественном состоянии каждое из них обязательно взаимодействует некоторым образом с другими телами, т.е. их перемещение в пространстве всегда ограничено внешними связями.
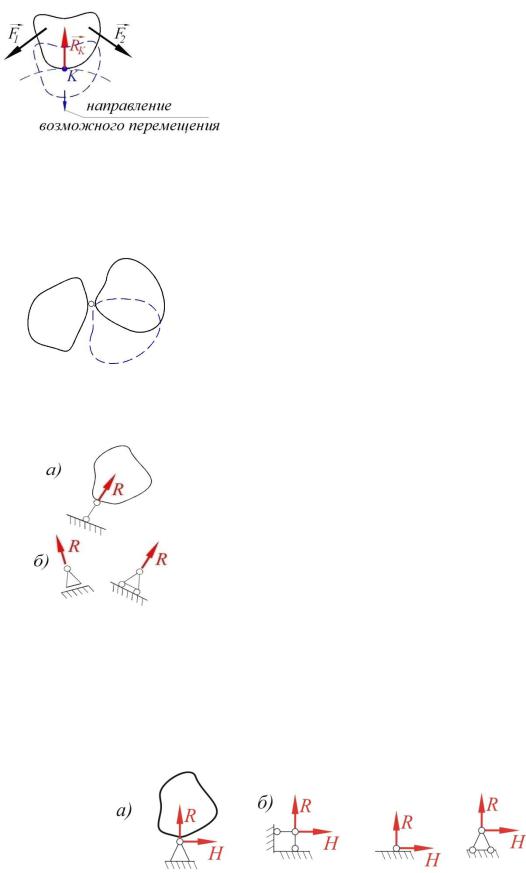
Аксиома освобождаемости от связей позволяет рассматривать несвободное твердое тело как свободное. Но при этом обязательно выполняется операция замены связей силами реакций связей (или замены связей их реакциями). Направление реакции связи всегда противоположно направлению, в котором связь препятствует движению тела (рис. 4.1).
Рис. 4.1.
Для понимания сути взаимодействия тел необходимо ввести понятие шарнирного соединения. Шарнирным соединением называется такой вид соединения тел между собой, при котором возможен беспрепятственный поворот одного тела относительно другого вокруг точки соединения.
Упрощенно шарнирное соединение изображают в виде окружности, к точкам которой примыкают соединяемые тела (рис. 4.2).
Для плоских задач различают следующие основные типы внешних связей: шарнирно-подвижная опора, шарнирно-неподвижная опора, жесткая заделка.
Рис. 4.2.
1. Шарнирно–подвижной опорой называется такой вид связи, который запрещает перемещение тела на плоскости только в одном из возможных линейных направлений.
Шарнирно-подвижную опору обычно условно изображают в виде абсолютно жесткого стержня, который при помощи двух шарниров соединяется с внешней средой и рассматриваемой конструкцией (рис. 4.3.а). Запрещенное линейное перемещение при этом совпадает с линией абсолютно жесткого стержня. При замене связи реакцией линия ее действия совпадает с направлением запрещенного перемещения. Также встречаются и другие изображения данной опоры (рис. 4.3.б).
Рис. 4.3.
2. Шарнирно–неподвижной опорой называется такой вид связи, который запрещает перемещение тела на плоскости во всех возможных линейных направлениях.
Шарнирно-неподвижную опору обычно условно изображают в виде двух абсолютно жестких стержней, которые жестко соединяется с внешней средой, и шарнирно соединяются с рассматриваемой конструкцией (рис. 4.4.а). В качестве запрещенных направлений линейных перемещений могут быть выбраны любые два взаимо-перпендикулярных направления. Также встречаются и другие изображения данной опоры (рис. 4.4.б).
Рис. 4.4.

23
3. Жесткой заделкой называется такой вид связи, который запрещает все возможные перемещения тела на плоскости.
|
Условное изображение жесткой заделки приведено на |
|
рис.4.5. В качестве запрещенных перемещений могут быть |
|
выбраны любые два взаимо-перпендикулярных направления |
|
линейных перемещений и поворот вокруг точки с |
Рис. 4.5. |
наложенной связью. |
|
Помимо указанных основных видов связей |
|
существуют и другие типы связей. В частности |
|
распространенным видом связи в механических системах |
Рис. 4.6. |
являются ползуны (рис. 4.6). |
|
4.2. ПОНЯТИЕ МОМЕНТА СИЛЫ, МОМЕНТ ПАРЫ СИЛ
Одним из важнейших понятий статики является момент силы, который характеризует вращательное воздействие силы на твердое тело.
Моментом силы относительно точки называют произведение модуля силы на плечо этой силы относительно данной точки.
Плечом силы является кратчайшее расстояние (длина перпендикуляра) от данной точки до линии действия силы.
Точка, относительно которой определяется момент, называется моментной. Момент силы имеет направление, которое определяется направлением поворота тела
относительно моментной точки по часовой или против часовой стрелки (рис. 4.7). Обычно знак плюс принято принимать в том случае, когда сила стремится повернуть тело вокруг точки против часовой стрелки.
Пусть твердое тело, к которому приложена сила Р (рис. 4.7) имеет одну закрепленную точку А, вокруг которой в плоскости чертежа оно может поворачиваться. В результате воздействия силы тело будет поворачиваться, т.е. сила создает в данном случае только вращательное воздействие, которое измеряется её моментом относительно центра А и согласно определению он равен произведению модуля силы
Р на плечо h, т.е MА(P) P h.
Рис. 4.7.
При этом вращение тела происходит по часовой стрелке и, следовательно, момент имеет алгебраический знак минус (-).
Математическая символика "МА(P)" читается следующим образом: момент силы Р относительно точки А (наименование точки указывается обязательно).
Если на тело действуют силы, лежащие в одной плоскости с центром, вокруг которого создается вращательный эффект, то моменты этих сил относительно центра могут выражаться алгебраическими их значениями.
Момент силы имеет три параметра: скалярную величину, плоскость поворота и направление поворота.
Единицей измерения скалярной величины момента силы, является «ньютонометр» (Н·м) или «килоньютонометр» (кН·м).
Моменты силы относительно центра, имеющие единую плоскость поворота, могут алгебраически складываться.

24
Рассматривая математическое значение вращательного эффекта силы, несложно сделать следующее утверждение: если линия действия силы проходит через центр, то момент этой силы относительно центра равен нулю, так как плечо силы относительно центра равно нулю.
Рассмотрим систему двух сил параллельных друг другу и направленных в противоположные стороны – антипараллельных сил (рис. 4.8).
Очевидно, что сумма проекций сил Р на произвольную ось будет равна нулю, т.е. представленная система сил не имеет равнодействующей. Величина суммарного момента сил относительно
точки Аопределится как: MА P a P (a b) P b.
Таким образом, суммарный момент двух сил Р не зависит от расстояния до моментной точки. Следовательно, суммарный момент для данной системы сил относительно любой точки на плоскости является постоянной величиной, равной произведению силы Р на расстояние между силами.Такая система сил называется парой сил.
Кратчайшее расстояние b (рис.4.8) между линиями действия сил, составляющих пару, называется плечом пары сил.
Действие пары сил на твердое тело характеризуется её моментом. Момент пары сил определяется произведением модуля одной из сил пары на её плечо: M P b .
На расчетных схемах приложенные к твердому телу пары сил изображаются условными знаками, которые указывают на направление поворота в плоскости расчетной схемы. При этом величина момента пары сил или указывается в условии задачи или её необходимо определить.
Момент пары сил (2.1) считают положительным, если пара сил стремится вращать плоскость чертежа в сторону, противоположную вращению часовой стрелки, и отрицательным – в сторону вращения часовой стрелки.
4.3. УСЛОВИЕ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ
Понятие момента силы дает возможность осуществлять перенос силы на плоскости не только по линии ее действия, но и параллельно самой себе. В этом случае при переносе силы P из точки А в точку B необходимо в точку B также добавить момент силы P относительно точки B (лемма о параллельном переносе).

25
Пусть на тело действует система сил, в которой силы расположены на плоскости произвольным образом (рис.4.9).
Выберем произвольную точку О, которую назовём центром приведения и, используя лемму о параллельном переносе силы, перенесем последовательно каждую силу системы параллельно самой себе в центр приведения. При этом каждый раз прибавляем момент переносимой силы относительно центра приведения. В результате выполнения таких операций мы получаем две системы сходящихся векторов. Одна из них состоит из совокупности векторов сил, которые по величине и направлению равны и параллельны соответствующим силам первоначальной системы, а вторая представляет собой совокупность добавленных векторных моментов переносимых сил относительно центра приведения.
(В целях упрощения на рис. 4.9 вторая система векторов изображена в виде системы моментов пар сил.)
Используя возможность замены системы сходящихся векторов одной равнодействующей и учитывая, что силы и моменты сил имеют разное физическое содержание, для системы сил получаем:
|
|
|
|
|
|
||||
R |
|
|
|
(4.1) |
P1 ... Pi ... Pn Pi |
||||
Для системы сходящихся векторных моментов равнодействующая равна:
|
|
|
|
|
|
|
|
|
(4.2) |
||||||
M o Mo (P1) ... Mo (Pi ) ... Mo (Pn ) Mo (Pi ) |
|||||||
|
|||||||
Таким образом, первоначальная система произвольно расположенных сил получила эквивалентную замену в виде одной результирующей силы и одного результирующего
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Pi ; |
M o |
|
M |
|
|
||
момента, т.е.: P1 |
... Pi ... Pn |
R |
(M i ) |
||||||||||
|
|
|
|
|
|
|
|
|
o |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следует заметить, что вектор силы, который входит составной частью в эквивалент, всегда приложен в центре приведения, а векторный момент как вторая часть эквивалента может быть представлен моментом пары сил и поэтому он является свободным вектором.
Главным вектором системы сил при приведении её к одному центру является векторная сумма всех сил системы.
Таким образом, можно утверждать, что главный вектор системы сил всегда приложен в центре приведения и его величина определяется через проекции всех сил системы на координатные оси, как модуль вектора равнодействующей системы сходящихся сил.
R*x Pix; |
R*y Piy. |
Главный момент системы сил при приведении её к одному центру представляет собой векторную суму моментов всех сил системы относительно выбранного центра приведения:
|
|
|
|
M o M o (Pi ).
Рассмотрим случай, при котором и главный вектор и главный момент системы сил равны нулю, т.е.: R* 0; MO* 0.

26
В этом случае твердое тело, на которое действует такая система сил, будет находиться в состоянии равновесия.
Исходя из значений главного вектора и главного момента системы сил, можно сформулировать условия равновесия твердого тела, на которое она действует: для того, чтобы абсолютно твердое тело под действием плоской системы произвольно расположенных сил находилось в состоянии равновесия, необходимо и достаточно, чтобы главный вектор и
|
n |
0; |
|
n |
|
Pi |
0. |
главный момент системы сил были равны нулю. R* Pi |
MO* |
mO |
|||||
|
i 1 |
|
|
i 1 |
|
|
|
Аналитически условия равновесия тела на плоскости можно сформулировать в виде
|
|
|
0; |
|
P |
|
|
||
|
ix |
|
0; |
(4.3) |
системы уравнений: Piy |
|
|||
|
|
|
(P ) 0. |
|
M |
0 |
|
||
|
|
i |
|
|
Следует отметить, что моментная точка для 3-го уравнения системы может выбираться произвольно.
4.4. СИСТЕМА СХОДЯЩИХСЯ И ПАРАЛЛЕЛЬНЫХ СИЛ
Рассмотрим два частных случая системы произвольно расположенных сил на плоскости в виде системы сходящихся сил и системы параллельных сил.
Пусть к некоторому абсолютно твердому телу приложена система сил, линии действия которых пересекаются в одной произвольной точке О (рис. 4.10). Приведем данную систему сил в точку О аналогично случаю для произвольной системы сил. В этом случае получим, что момент каждой силы системы относительно точки О равен нулю. Таким образом,
главный момент системы сил M o 0. Для соблюдения условия равновесия в этом случае необходимо приравнять главный вектор системы сил к нулю
|
n |
0. |
R* Pi |
||
Рис. 4.10. |
i 1 |
|
|
|
|
Очевидно, что в этом случае момент, создаваемый главным вектором системы сил, относительно любой точки на плоскости также будет равен нулю. Таким образом, условие равновесия абсолютно твердого тела при действии на него системы сходящихся сил может быть сформулировано следующим образом: для того, чтобы абсолютно твердое тело под действием плоской системы сходящихся сил находилось в состоянии равновесия, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси плоской системы координат, в которой лежит система, были бы равными нулю Pix 0; Piy 0.
Рассмотрим теперь систему параллельных сил. Пусть к некоторому абсолютно твердому телу приложена система сил, линии действия которых параллельны между собой (рис. 4.11). Рассуждая аналогично предыдущим случаям, приведем систему сил в произвольную точку О. В этом случае получим некоторый главный момент системы сил
|
|
|
|
n |
M o M o |
(Pi ) и главный вектор системы сил R* Pi . |
|||
i 1

27
Однако, поскольку силы параллельны для определения главного вектора системы сил выберем систему координат, в которой ось y параллельна силам Р, а ось х – перпендикулярна. Очевидно, что в этом случае сумма проекций все сил системы на ось х равна нулю
Pix 0.
Тогда условие равновесия абсолютно твердого тела при действии на него системы параллельных сил может быть сформулировано следующим образом: для того, чтобы абсолютно твердое тело под действием плоской системы параллельных сил находилось в состоянии равновесия,
Рис. 4.11. необходимо и достаточно, чтобы алгебраическая сумма
проекций всех сил на параллельную ось была бы равной нулю и алгебраическая сумма моментов всех сил системы относительно любой точки, лежащей в плоскости действия сил, была бы также равной нулю Piy 0; MO Pi 0.
Условия равновесия (2.4) могут быть использованы при определении опорных реакций. При решении системы уравнений равновесия некоторые неизвестные силы могут оказаться отрицательными. Это означает, что направление этой силы противоположно тому, которое было изображено на рисунке расчетной схемы.
Также следует учитывать, что для частных случаев плоской системы количество расчетных уравнений различно: для системы сходящихся сил – 2 расчетных уравнения, определяемых условием равновесия тела при действии системы сходящихся си; для системы параллельных сил – 2 расчетных уравнения, определяемых условием равновесия тела при действии системы параллельных сил;
Оси декартовых координат целесообразно направлять так, чтобы одна из них оказалась параллельной всем силам, приложенным к твердому телу. Уравнение моментов рекомендуется составлять относительно точки, лежащей на линии действия неизвестной силы. Это даёт возможность, минуя решение системы уравнений равновесия, определить одну из неизвестных величин непосредственно из уравнения моментов.
Правильность решения задачи можно проверить, составив уравнение моментов всех сил (включая и те, которые определены решением задачи) относительно любой точки, которая лежит в плоскости действия сил и не лежит на линии действия тех сил, которые определяются. Если такое уравнение обращается в тождество типа «0=0», то задача решена верно.
ЛЕКЦИЯ № 5. ВНУТРЕННИЕ УСИЛИЯ В БРУСЕ, МЕТОД СЕЧЕНИЙ, ЭПЮРЫ ПРОДОЛЬНЫХ СИЛ В СТЕРЖНЕ. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ, ЗАКОН ГУКА.
5.1. ВНУТРЕННИЕ УСИЛИЯ В БРУСЕ, МЕТОД СЕЧЕНИЙ, ЭПЮРЫ ПРОДОЛЬНЫХ СИЛ В СТЕРЖНЕ.
Анализируя окружающие нас предметы, мы замечаем, что струна гитары и канат лифта растянуты. Колонны зданий, ножки стула, на котором мы сидим, сжаты. Это самые простые и очевидные виды деформаций растяжения и сжатия.
Связность тела в недеформированном состоянии обусловливается тем, что между его атомами существуют силы взаимодействия, и каждый атом находится в равновесии под действием приложенных к нему сил. Внешние силы вызывают деформацию тела, следовательно, меняются расстояния между атомами, меняется взаимное расположение

28
атомов, меняются и силы взаимодействия между атомами. Изменение сил взаимодействия между атомами вследствие деформации мы будем называть внутренними усилиями, сопровождающими деформацию. Однако одного понятия внутренних усилий в этом случае будет мало, поскольку эти усилия могут иметь совершенно различные направления, а также создавать моменты сил, учет которых необходим при рассмотрении состояния равновесия тела. Поэтому, говоря о внутренних усилиях, будем употреблять понятие внутреннего силового фактора. Внутренний силовой фактор – есть некоторая обобщенная сила или момент силы, возникающие в сечении бруса, обусловленные силами взаимодействия элементов кристаллической решетки при ее деформации.
Изучая деформации растяжения и сжатия, будем для начала рассматривать такие загружения стержней, при которых равнодействующие всех сил и реакций лежат на одной прямой, совпадающей с продольной осью элемента. В этом случае в поперечном сечении элемента возникает один внутренний силовой фактор – продольное усилие N (продольная сила).
Для определения внутренних усилий (продольных сил) используется метод сечений, сущность которого заключается в следующем (рис. 5.1).
Алгоритм метода сечений:
1.мысленно рассекаем стержень плоскостью, перпендикулярной продольной оси (m-n) стержня на две части и одну из частей заменяем действующими внутренними усилиями;
2.рассматриваем в равновесии одну из частей: верхнюю или нижнюю, правую или левую (в данном случае нижнюю); возникающее в сечении неизвестное усилие N, считаем положительным и направляем в сторону от сечения (в сторону отброшенной части);
3.записываем уравнение равновесия для рассматриваемой части элемента:
ΣFz = 0 Nz– P = 0, откуда Nz= P;
4.Полученный в результате решения знак «+» свидетельствует о том, что усилие растягивающее,
знак минус – сжимающее.
Следовательно, метод сечений – алгоритм последовательных действий, с помощью которых определяют внутренние усилия.
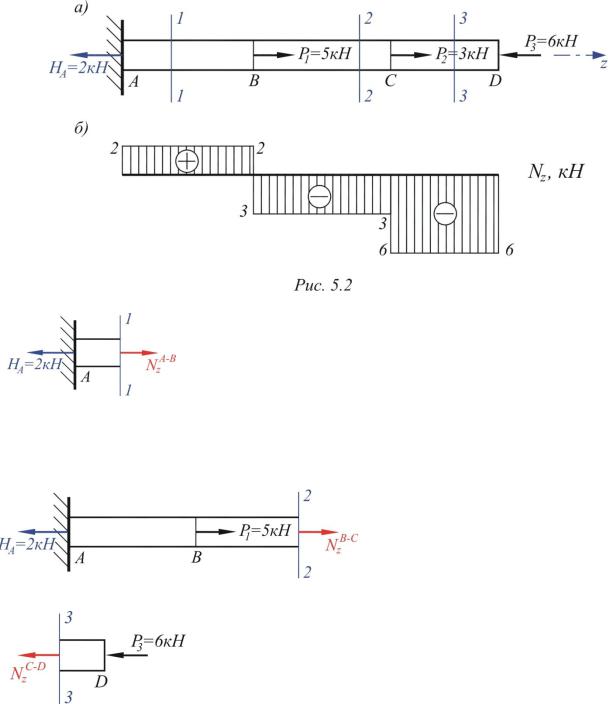
При приложении к стержню нескольких внешних сил, величина продольного усилия в стержне может изменяться в зависимости от расположения расчетного сечения. Рассмотрим стержень, представленный на рис. 5.2.а. К стержню приложены три силы Р1, Р2, Р3, находящиеся на одной прямой. Очевидно, что для такой системы сил условия равновесия имеют вид Fz 0. Запишем это уравнение и определим реакцию опоры в точке А:
Fz P1 P2 P3 HA 0, откуда HA P1 P2 P3 5 3 6 2кН.
Определив опорные реакции, можно приступить к определению внутренних усилий в стержне. Разделим стержень на отдельные участки в точках приложения внешних нагрузок, т.е. получаем три участка – А-В, В-С, С-D.
29
В соответствии с методом сечений рассечем стержень на две части сечение 1-1 и рассмотрим в равновесии левую отсеченную часть. Неизвестную продольную силу в сечении направляем в сторону растяжения (в сторону отброшенной части). Из условия равновесия получим
Fz NzA B HA 0, откуда
NzA B HA 2кН
Аналогично в сечении 2-2, получимFz NzB C P1 HA 0, откуда
NzB C HA P1 2 5 3кН
При рассечении сечением 3-3 на участке С-D, рассмотрим в равновесии правую отсечную часть:Fz NzC D P3 0, откуда
NzC D P3 6кН.
Очевидно, что на расчетные уравнения, а равно и на величину продольного усилия в элементе, место расположения сечения на каждом участке влияния не оказывает. Следовательно, величина продольного усилия на каждом участке постоянна. Построим диаграмму изменения продольного усилия по длине стержня (рис. 5.2.б). Такая диаграмма называется эпюрой продольной силы.
Эпюра – это диаграмма изменения какой-либо величины (усилия, напряжения, деформации и т. д.) по длине элемента или по высоте (ширине) поперечного сечения.
Ордината эпюры в определенном масштабе равна численному значению продольного усилия в рассматриваемом сечении элемента.
Положительные значения продольных усилий откладываются вверх от оси, отрицательные – вниз в определенном масштабе или, как правило, соразмерно значениям величин усилий. На эпюрах обязательно ставят знаки, обозначая положительную и отрицательную область эпюры. При этом сами значения ординат могут быть записаны по

30
модулю. Также следует помнить, что обязательно должна быть указана величина, для которой построена эпюра, на участках с постоянной величиной значения указывают в начале и в конце участка, штриховка эпюры производится сплошными линиями, перпендикулярно оси элемента.
5.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ. ЗАКОН ГУКА
Определение внутренних силовых факторов в элементах конструкций еще не дает возможности судить о прочности конструкции. Известно, что один и тот же груз может с легкостью порвать тонкий канат и удерживаться на более толстом. Поэтому для расчетов на прочность необходимо иметь удельное внутреннее усилие, т.е. усилие, действующее на единицу площади поперечного сечения. Эта величина получила название напряжений. Напряжения – это усилие, действующее на единицу площади.
Если напряжения определяются в поперечном сечении стержня в направлении продольной оси, то такие напряжения имеют название нормальные напряжения, поскольку направлены по нормали к плоскости сечения. По поверхности поперечного сечения напряжения могут распределяться равномерно и неравномерно (по какому-то закону). На основании определения можно записать
z |
|
dNz |
, |
(5.1) |
|
dF |
|||||
|
|
|
|
где dNz – величина усилия (элементарное усилие), приходящееся на некоторую бесконечно малую (элементарную) площадку dF.
Единицами измерения напряжений являются мегапаскаль МПа . Напомним, что
1МПа 1 Н . |
|
|
м2 |
|
|
В основе расчета на прочность (3.1) стержней в случае сжатия растяжения лежит |
||
условие: |
|
|
z |
R, где |
(5.2) |
R – расчетное сопротивление – величина максимально допустимых напряжений в элементе, при которых прочность считается обеспеченной.
ЗАМЕЧАНИЕ. В настоящем курсе величина расчетного сопротивления R будет задана для каждого конкретного материала конструкции. Однако следует знать, что в курсах строительных конструкций (железобетонных, металлических и пр. расчетное сопротивление будет также зависеть от вида расчетной схемы, ответственности конструкции и пр., иными словами от необходимого уровня надежности полученных результатов расчета.
Рассмотрим стержень с постоянной площадью поперечного сечения F, к концам которого приложена распределенная нагрузка (рис. 5.3). На некоторую бесконечно малую (элементарную) площадку dF действует некоторое усилие dNz. Просуммировав все такие площадки по всему сечению, получим результирующую величину продольной силы Nz в стержне:
Nz dNz |
z dF |
(5.3) |
F F
