
konsp_lektsiy_1ch
.pdf
11
|
|
|
Труба |
|
прямоугольная |
||
|
|
|
характеризуется |
размерами |
|||
|
|
|
внешних граней h, b и |
||||
|
|
|
толщиной стенки t. В |
||||
Труба |
|
|
условном |
|
обозначении |
||
|
Тр.80х60х8 |
указываются три эти размера |
|||||
прямоугольная |
|
||||||
|
сечения |
в |
миллиметрах. |
В |
|||
(квадратная) |
|
|
случае |
квадратной трубы, |
|||
|
|
|
|||||
|
|
|
когда h=b, в условном |
||||
|
|
|
обозначении |
также приводят |
|||
|
|
|
три размера, два из которых |
||||
|
|
|
одинаковы. |
|
|
|
|
|
|
|
Круглое сечение характеризу- |
||||
|
|
|
ется |
только |
внешним |
||
Круг |
|
30 |
диаметром D. В условном |
||||
|
обозначении |
|
указывают |
||||
|
|
|
внешний |
|
диаметр |
в |
|
|
|
|
миллиметрах. |
|
|
||
|
|
|
Квадратное |
|
сечение |
||
|
|
|
характеризуется |
размером |
|||
|
|
20 |
грани квадрата b. В условном |
||||
Квадрат |
|
обозначении |
указывают этот |
||||
|
размер в миллиметрах. |
|
|||||
|
|
|
|
|
|
|
|
ЛЕКЦИЯ № 2. ЗАВИСИМОСТЬ МЕЖДУ ГЕОМЕТРИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ПРИ ПРЕОБРАЗОВАНИИ СИСТЕМЫ КООРДИНАТ. ПОНЯТИЕ ЦЕНТРА ТЯЖЕСТИ И ГЛАВНЫХ ОСЕЙ ИНЕРЦИИ СЕЧЕНИЯ
2.1. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ОСЕЙ. ПОНЯТИЕ ЦЕНТРА ТЯЖЕСТИ
Геометрические характеристики сложных составных сечений непосредственным интегрированием вычислять затруднительно. Можно разбить составную фигуру на отдельные простейшие, для которых геометрические характеристики уже известны, и интегрирование заменить суммированием. При этом возникает необходимость знать зависимости между геометрическими характеристиками плоских сечений при параллельном переносе и повороте системы координат вокруг ее начала.
Рассмотрим случай параллельного переноса координатных осей. Вычислим статический момент площади относительно оси х1, смещенной параллельно на расстояние a от прежней оси x, относительно которой статический момент площади Sx известен:
Sx1 y1dF (y a)dF ydF a dF Sx aF . |
|
|||
F |
F |
F |
F |
|
При некотором расстоянии между осями ac статический |
Рис.2.1 |
|||
момент площади окажется равным нулю. Положив Sx1=0, |
||||
найдем |
|
|
|
|
ac |
Sx |
(2.1) |
|
F |
|||
|
12
Ось, относительно которой статический момент равен нулю, называется центральной. Пересечение центральных осей определяет точку называемую центром тяжести.
Из (2.1) следует, что при известном положении центра тяжести фигуры, статический момент площади можно вычислить не прибегая к интегрированию, т.е.
Sx ycF , |
Sy xcF , |
(2.2) |
где xc, yc – координаты центра тяжести фигуры.
Для составной фигуры: Sx yi Fi |
yc Fi , |
Sy xi Fi |
xc Fi , откуда |
xiFi xc Fi ;
(2.3)
yiFi yc Fi .
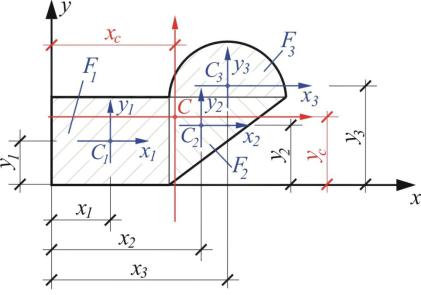
Рассмотрим порядок определения центра тяжести (2.2) на примере произвольной фигуры, показанной на рис. 2.2.
1.Фигура разбивается на простейшие, для которых просто определяются площади (F1, F2, F3) и центры тяжести (C1, C2, C3).
2.Вводится некоторая
вспомогательная |
система |
|
||
координат (произвольно). |
|
|
||
3. Определяются координаты |
|
|||
центров |
тяжести |
каждой |
|
|
простой |
фигуры |
в |
|
|
вспомогательной |
системе |
|
||
координат (xi, yi). |
|
|
|
|
4. Вычисляются координаты |
|
|||
центра |
тяжести |
фигуры |
|
|
(xc, yc) по формулам (2.3). |
|
|
||
5. По полученным координа- |
Рис.2.2 |
|||
там определяется |
точка |
|
||
центра тяжести на чертеже.
Заметим, что если фигура имеет ось симметрии, то центр тяжести всегда находится на этой оси. Если таких осей две, например прямоугольник, двутавр и пр., то центром тяжести является точка пересечения этих осей. Также следует отметить, что любая ось, проходящая через центр тяжести является центральной осью. Таким образом, количество центральных осей для сечений бесконечно.
В дальнейшем за исходную систему координат будем принимать систему центральных осей. Пусть в некоторой системе центральных осей Xc, Yc осевые моменты инерции известны (рис. 2.3). Требуется вычислить моменты инерции в системе координат, поступательно смещенных на расстояние a и b относительно прежней системы.

|
|
|
13 |
|
Осевые моменты инерции определяются по формуле |
|
|||
(1.2): |
|
|
|
|
Ix y2dF a y1 2dF a2F 2a y1dF y12dF |
|
|||
F |
F |
F |
F |
|
a2F 2aSx |
Ix . |
|
|
|
|
c |
c |
|
|
Поскольку ось xc – центральная, то Sx |
0. Тогда |
|
||
|
|
c |
|
|
Ix Ix |
a2F. |
|
(2.4) |
|
c |
|
|
|
|
Аналогично рассуждая, нетрудно почить остальные |
Рис.2.3 |
|||
зависимости между моментами инерции: |
|
|||
Iy Iy |
b2F; |
|
|
|
c |
|
|
|
(2.5) |
|
|
|
|
|
Ixy Ixcyc abF.
Выражения (2.4) и (2.5) представляют собой зависимости между моментами инерции при параллельном переносе системы координат. Следует отметить, что расстояния a и b являются координатами точки начала координат, и, как и любые координаты, могут принимать как положительные, так и отрицательные значения.
Например, определим моменты инерции прямоугольника относительно системы координат, проходящей через его стороны (рис. 2.4).
Как известно из предыдущей темы, моменты инерции прямоугольника относительно центральных осей имеют вид:
Ix |
|
bh3 |
; Iy |
|
hb3 |
; Ix y |
0. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
c |
12 |
c |
|
12 |
|
c |
c |
|
|
|
|
|
|
|
|
|
|||
Тогда в соответствии с (2.4) и (2.5) получим |
|
|
|||||||||||||||||
|
|
|
2 |
|
|
|
bh3 |
|
|
|
h 2 |
bh3 |
bh3 |
bh3 |
|||||
Ix Ix |
a |
F |
|
|
|
|
|
|
bh |
|
|
|
|
|
, |
||||
|
|
12 |
4 |
3 |
|||||||||||||||
|
|
c |
|
|
12 |
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
hb3 |
|
|
|
b 2 |
|
hb3 |
|
hb3 |
|
hb3 |
||||||||
Iy |
Iyc |
b |
F |
|
|
|
|
|
bh |
|
|
|
|
|
|
|
||||||
12 |
2 |
12 |
|
4 |
3 |
|
||||||||||||||||
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.4 |
|
|
|
|
|
|
|
h |
|
|
|
b |
|
h2b2 |
|
|
|
|
||||||
Ixy |
Ix y |
abF 0 |
|
|
|
|
|
|
|
|
bh |
|
|
|
. |
|
|
|
|
|||
|
|
2 |
|
|
4 |
|
|
|
|
|
||||||||||||
|
c c |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.2. ПОВОРОТ КООРДИНАТНЫХ ОСЕЙ
Пусть для некоторой фигуры в системе координат x, y моменты инерции площади Ix, Iy, Ixy известны. Вычислим моменты инерции площади этой фигуры в системе координат x1, y1, повернутой на положительный угол по отношению к исходной системе координат (рис. 2.5). При этом угол будем считать положительным, если поворот системы координат производится против часовой стрелки.

14
Очевидно, что AOB= CAD= , как углы между взаимно перпендикулярными прямыми. Тогда
y1 CB CA AB ADcos OAsin ,
откуда получим
y1 ycos xsin .
Аналогично для другой координаты
x1 OB CD OAcos ADsin ,
откуда
x1 xcos ysin .
Согласно определению осевой момент инерции определится как:
Рис.2.5
Ix1 y12dF ycos xsin 2 dF cos2 y2dF sin2 x2dF 2sin cos xydF .
F F F F F
Подставив уже известные интегральные зависимости, получим
Ix |
Ix |
cos2 Iy sin2 |
Ixy sin 2 . |
(2.6) |
1 |
|
|
|
|
Аналогично определится значение осевого момента инерции относительно оси y1: |
|
|||
Iy |
Iy |
cos2 Ix sin2 |
Ixy sin 2 . |
(2.7) |
1 |
|
|
|
|
Найдем сумму полученных осевых моментов инерции, сложив выражения (2.6) и (2.7):
Ix1 Iy1 Ix cos2 Iy sin2 Ixy sin 2 Iy cos2 Ix sin2 Ixy sin 2Ix cos2 sin2 Iy cos2 sin2 Ix Iy.
Очевидно, что как бы ни была повернута система координат x1, y1 по отношению к исходной системе координат x, y сумма осевых моментов инерции не изменяется. Это утверждение также согласуется определением полярного момента инерции площади, который согласно равен сумме осевых моментов инерции площади, т.е.
Ix |
Iy |
Ix Iy |
I |
const. |
(2.8) |
1 |
1 |
|
|
|
|
Центробежный момент инерции площади в системе координат x1, y1 определится как:
Ix1y1 x1y1dF xcos ysin ycos xsin dF cos sin y2dF
F F F
cos sin |
|
x2dF cos2 sin2 |
xydF cos sin I |
x |
I |
y |
|
|
|
|
|
|
|||
|
F |
F |
|
|
|
|
|
cos2 sin2 Ixy.
Откуда получим
Ix y |
|
Ix |
Iy |
sin2 Ixy cos2 . |
(2.9) |
|
|
2 |
|||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||
Полученные формулы (2.4)-(2.8) в принципе решают поставленную задачу вначале настоящей темы: определить геометрические характеристики относительно любой системы координат, если известны эти характеристики относительно какой-то системы координат. Однако на практике при решении инженерных задач, как правило, нужно знать, как нужно расположить систему координат, чтобы, например, получить максимальный осевой момент инерции площади или нулевой центробежный момент инерции площади. В этом случае используется понятие главных осей инерции.

15
Главными осями инерции называется пара осей, относительно которой
центробежный момент инерции площади равен нулю.
Действительно, осевые моменты инерции площади Ix, Iy всегда положительны как суммы положительных слагаемых, а центробежный момент инерции площади Ixy может быть и положительным, и отрицательным, и, как следствие, нулевым. Таким образом, система осей x, y, относительно которой Ixy=0 называется главной, а оси главными осями инерции.
Главные оси инерции, проходящие через центр тяжести сечения, называют главными центральными осями инерции.
Найти положение главных осей инерции не сложно. Для этого достаточно воспользоваться выражением (2.9). Итак, пусть имеется некоторая система координат x, y, в которой все моменты инерции площади известны (рис. 2.5). Найдем угол 0, на который необходимо повернуть исходную систему координат, чтобы получить систему координат u, v, относительно которой Iuv=0. На основании (2.9)
Iuv |
|
Ix |
Iy |
sin2 |
0 Ixy cos2 0 |
0, |
||
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
tg2 0 |
|
2Ixy |
. |
(2.10) |
|
|
|
|
|
|||||
|
|
|
|
|
|
Iy Ix |
|
|
Уравнению (2.10) удовлетворяют два значения 2 0, отличающиеся на 1800 или два значения 0, отличающиеся на 900. Таким образом, уравнение (2.10) дает нам положение двух осей, составляющих между собой прямой угол. Это и будут главные оси инерции u и v.
Главные оси инерции обладают очень важным качеством – осевые моменты инерции площади относительно этих осей имеют экстремальные значения. Убедится в этом не
сложно. Достаточно исследовать на экстремум функцию Ix1 , приведенную в (2.6),
dIx1 Ix 2cos sin Iy 2sin cos Ixy 2cos2 0, d
Ix Iy sin 2 Ixy 2cos2 0,
tg2 2Ixy . Iy Ix
Очевидно, что экстремальные значения будут при угле = 0, определяемое по (2.10). Значит осевые моменты инерции Iu и Iv – экстремальные, т.е. Iu > Ix, Iy > Iv.
Следует отметить, что если за исходную систему координат принять систему главных осей инерции u, v, то выражения (2.6)-(2.8) преобразуются к виду.
Ix |
Iu cos2 Iv |
sin2 , |
(2.11) |
|||
Iy |
Iu sin2 |
Iv |
cos2 , |
(2.12) |
||
|
Ixy |
Iu |
Iv |
sin2 . |
(2.13) |
|
|
|
2 |
||||
|
|
|
|
|
|
|
Величины осевых моментов инерции площади можно вычислить по формулам (2.6), (2.7) предварительно определив угол поворота систему координат по формуле (2.10). Однако можно обойтись и без вычислений угла. С этой целью используем зависимости (2.10)-(2.12). Вычтем из (2.11) выражение (2.12)
Ix Iy Iu Iv cos2 . |
(2.14) |
Используя (2.10), имеем

|
|
|
|
|
16 |
|
|
|
|
cos2 |
1 |
|
|
|
Ix Iy |
||||
|
|
|
|
|
|
|
|
||
1 tg2 2 |
|
Ix Iy |
2 4Ixy2 . |
||||||
|
|
|
|
||||||
Поставляя полученное выражение в (2.14), получим
Ix Iy |
Iu Iv |
|
Ix Iy |
|
, |
||
|
|
|
|
||||
|
Ix Iy 2 4Ixy2 |
||||||
|
|
|
|
|
|
||
Iu |
Iv |
Ix |
Iy 2 4Ixy2 |
. |
(2.15) |
||
На основании (2.8) запишем условие инвариантности суммы осевых моментов инерции площади:
Ix Iy Iu Iv .
Суммируя и вычитая последнее равенство с (2.15) получим
|
|
|
Ix |
Iy |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|||||
Iu |
|
|
|
|
|
|
|
|
Ix Iy |
4Ixy |
, |
|
|
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
(2.16) |
||
|
|
|
Ix |
Iy |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||||
Iv |
|
|
|
|
|
|
|
|
Ix Iy |
4Ixy . |
||
|
2 |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
Иногда, для сокращения записей формулы (2.16) записывают в виде:
|
Ix Iy |
|
1 |
|
|
|
|
|
|
2 |
2 |
|
|||
Iu,v |
|
|
|
|
Ix Iy |
4Ixy . |
|
|
2 |
||||||
2 |
|
|
|
|
|
||
Имея значения осевых моментов инерции относительно главных осей Iu, Iv можно найти угол наклона каждой из главных осей к оси x исходной системы координат:
|
|
|
|
|
|
|
|
|
tg2 |
|
2tg |
|
|
2Ixy |
|
, откуда |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Iy |
Ix |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 tg |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Iy |
Ix |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
|
|
|
tg 1 0. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ixy |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Корни этого уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
Ix |
Iy |
|
|
Ix |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
tg 1,2 |
|
|
|
Iy |
|
4 |
|
Iy |
|
Iy |
Ix 2 4Ixy2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
Ixy |
|
Ixy |
|
|
|
|
|
|
2Ixy |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.17) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
Ix Iy |
|
|
|
|
|
Iu,v Iy |
. |
|
|
|
|
||||||||||||||||||
|
Iy Ix 2 4Ixy2 |
|
|
2Iy |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2Ixy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ixy |
|
|
|
|
|
|
|
|
Однако, корень 1, полученный подстановкой в выражение (2.17) Iu дает положение оси v, и наоборот, корень 2, полученный подстановкой в выражение (2.17) Iv дает положение оси u. Дабы избежать путаницы используем условие 1- /2= 2, и углы до соответствующих осей обозначим u и v. Тогда
|
|
|
|
|
|
|
|
Ixy |
|
|
|||
tg u |
tg 2 |
tg( 1 |
|
|
|
) ctg 1 |
|
|
|
. |
(2.18) |
||
2 |
|
Iy |
Iu |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Ixy |
|
|
||||
tg v |
tg 1 |
tg( 2 |
|
|
) ctg |
2 |
|
|
|
. |
(2.19) |
||
2 |
Iy |
Iv |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
Формулы (2.18), (2.19) наиболее удобны в плане практического использования, поскольку четко отражают какой угол, к какой из осей необходимо откладывать. Как и в формуле (2.10) положительный угол откладывается от оси x в направлении против часовой

17
стрелки. Однако формулы (2.18), (2.19) возможно использовать только при условии, что осевые моменты инерции площади относительно главных осей известны, либо они должны быть предварительно вычислены по (2.16). Формула (2.10) позволяет вычислить угол до одной из главных осей инерции (причем какая это ось формула не указывает) без определения осевых моменты инерции площади относительно главных осей инерции.
В заключении следует отметить, что если хотя бы одна из координатных осей сечения является осью симметрии, то центробежный момент инерции площади будет равен нулю, и, как следствие, такие оси будут главными осями инерции. Очевидно, что для фигур, имеющих много осей симметрии (круг, квадрат, правильные многоугольники и пр.) количество главных осей может быть больше двух.
ЛЕКЦИЯ № 3. ОБЩИЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ. ОСНОВНЫЕ ПОНЯТИЯ СТАТИКИ. АКСИОМЫ СТАТИКИ. СИСТЕМА СИЛ.
Теоретическая механика изучает равновесие и движение твердого тела; состоит из трех частей: статики, кинематики, динамики. Сопротивление материалов и строительная механика изучают методы расчетов на прочность, жесткость и устойчивость соответствующих конструкций.
3.1. ОСНОВНЫЕ ПОНЯТИЯ СТАТИКИ ТВЕРДОГО ТЕЛА
Статика - это учение о равновесии тел под действием приложенных к ним сил. Равновесию тела соответствует равновесие сил, поэтому статика есть одновременно учением о равновесии сил, действующих на тело.
Сила – это мера механического взаимодействия между материальными объектами. Сила определяет интенсивность взаимодействия (некоторое её количественное
значение), его пространственную направленность и то место в пространстве, в котором взаимодействие происходит. Таким образом, сила имеет три основных параметра, - величину, направление и место (точку) действия, - и поэтому ее математически можно обозначить некоторой векторной величиной, которая имеет скалярное значение, направление и точку приложения. Количественное значение силы в системе СИ имеет размерность «Ньютон» («Н»). При решении задач, связанных со строительными конструкциями, как правило, силы имеют значения тысяч Ньютон, поэтому наиболее удобно использовать производную единицу - «килоНьютон» («кН»).
 P3
P3 



 P1
P1
 P2
P2
На расчетных схемах при решении инженерных задач сила показывается в виде вектора (рис. 1.1), который обязательно характеризуется точкой приложения.
Силы, являясь мерой механического воздействия между материальными объектами, по характеру его проявления и по условиям решения какой-либо задачи классифицируются как сосредоточенные и распределенные, внешние и внутренние, активные и реактивные.
Рис.3.1
Сосредоточенная сила – это характеристика механического взаимодействия между двумя телами, которое происходит в одной конкретной точке рассматриваемого тела. Она изображается на схемах как вектор, приложенный к конкретной точке тела (рис.3.1).

18
Распределенная сила – это характеристика механического взаимодействия между двумя телами, которое происходит по линии или по поверхности.
Для распределенной силы должна быть обязательно известна ее интенсивность – некоторая сила, отнесенная к единице длины или площади поверхности распределения.
q1 f (L); |
q2 f (S). |
||||||||
где: |
q |
|
H |
; q |
H |
– интенсивность силы; при этом L и S – длина и площадь |
|||
|
|
|
|
|
|||||
|
2 |
|
2 |
||||||
|
1 |
|
|
|
|||||
|
|
м |
м |
|
|
|
|||
распределения силы.
При решении инженерных задач методами статики распределенную силу заменяют сосредоточенной. При этом модуль сосредоточенной силы определяется как площадь или объем фигуры распределения силы, а ее точка приложения лежит в центре тяжести фигуры или объема фигуры распределенной силы (рис. 3.2).
à) |
|
á) |
Q= |
q1xL |
â) |
Q=q2xS |
12 L |
Q=q1xL |
23L |
2 |
q |
|
|
|
q |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
L |
|
L |
|
|
q2 |
|
|
|
|
|
Рис.3.2. Распределенная сила: а) равномерно по длине; б) неравномерно по длине; в) равномерно по площади
Внешней силой называется такая сила, которая проявляется в результате взаимодействия рассматриваемого тела с другими телами, которые в данный момент не рассматриваются.
Внутренняя сила характеризует взаимодействие между собой отдельных материальных частиц, принадлежащих рассматриваемому телу. Если рассматривается не одно материальное тело, а их система, то в этом случае взаимодействие между телами системы также относится к понятию внутренних сил.
Активными силами называются такие силы, которые проявляются в результате воздействия на рассматриваемое тело со стороны других тел и которые стремятся изменить состояние рассматриваемого тела.
Реактивные силы проявляются со стороны тех тел и материальных объектов, которые стремятся удержать рассматриваемое тело в прежнем состоянии.
На одно и то же твердое тело могут действовать сразу несколько других тел и тогда механическое взаимодействие каждого из них, определяемое силой, создает систему сил. Так на рис. 3.1 показано, как к некоторому абсолютно твердому телу приложено несколько сосредоточенных сил. Совокупность этих сил определяет систему сил. Однако если две силы приложены к разным телам, то они не являются системой сил.
Система сил – это совокупность сил, приложенных к одному телу.
Система сил, которая не изменяет состояния тела, называется уравновешенной системой
сил.
Одним из ключевых понятий теоретической механики является понятие внешних связей. Внешней связью называется тело, ограничивающее движение данного, рассматриваемого нами тела. Примеры связей: стол, поддерживающий книгу; рельсы, на которые опирается железнодорожный вагон; трос, на котором висит груз; подшипник, в котором вращается вал и т.д. В машинах и конструкциях для любой детали связями являются все другие детали, которые с ней взаимодействуют.
В качестве примера рассмотрим фонарь, закрепленный при помощи двух тросов в точках А и В (рис. 3.3).

19

 Â
Â
S2 
Ðèñ. 1.3
S |
Фонарь обладает некоторым собственным весом G, который |
|
можно представить в виде сосредоточенной силы, приложенной |
À |
в центре тяжести фонаря. Сила G является внешней силой по |
|
отношению к рассматриваемой системе, поскольку она |
|
обусловлена взаимодействием рассматриваемого тела – фонаря, с |
|
другим телом – Землей, которое в данный момент не |
|
рассматривается. Сила G является активной силой, так как |
|
стремится изменить положение фонаря. Однако в результате |
|
наличия тросов, закрепленных в точках А и В к некоторой |
|
внешней конструкции, положение фонаря не изменяется. Таким |
G |
образом, тросы в точках А и В имеют внешние связи. |
Рис.3.3.
Отсутствие изменения состояния фонаря во времени позволяет также говорить о том, что к фонарю приложена уравновешенная система сил. При этом силы S1 и S2, позволяющие уравновесить вес фонаря G, появляются в связях и носят название реакций связей.
Реакцией связи называется механическое взаимодействие рассматриваемого тела с тем телом, которое ограничивает его перемещение. Направление реакции связи противоположно направлению, в котором внешняя связь препятствует движению тела. Если в месте соприкосновения тела и связи отсутствует трение, то связь называется идеальной связью.
3.2. АКСИОМЫ СТАТИКИ
Все основные положения статики выводятся на основании нескольких аксиом, которые сформулированы на основе наблюдения и изучения явлений окружающего нас реального мира.
Аксиома инерции: под действием уравновешенной системы сил тело находится в состоянии покоя или движется прямолинейно и равномерно.
Аксиома равновесия двух сил: тело находится в состоянии равновесия, если к нему приложены две равные по величине и противоположные по направлению силы, имеющие общую линию действия.
|
|
Прямая A-B, вдоль которой действуют |
|
 |
P |
силы P, называется линией действия |
|
силы. |
|||
|


 À
À
P 









Рис.3.4.
Аксиома присоединения или исключения уравновешенных систем сил: состояние абсолютно твердого тела не изменится, если к нему присоединить или отбросить уравновешенную систему сил.
Проиллюстрировать суть аксиомы присоединения или исключения уравновешенных систем сил можно на основе рис. 3.5. Пусть некоторому абсолютно твердому телу была приложена уравновешенная система сил P. Добавим к этому телу дополнительную систему сил F. Тогда, если система сил F является уравновешенной, то состояние абсолютно твердого тела не изменится.

20
F
Ð1 








 Ð2
Ð2
 Ð2
Ð2
Рис.3.5.
|
На основании этой аксиомы можно доказать |
|
справедливость утверждения о том, что силу можно |
Ð |
переносить вдоль линии ее действия в любую точку. |
1 |
Такое действие не изменит состояние тела, на которое |
F |
она действует. При этом следует отметить, что |
|
подобное действие, а также и сама аксиома |
|
присоединения или исключения уравновешенных |
|
систем сил, имеет место только для абсолютно |
|
твердого тела. |
Аксиома параллелограмма сил: если линии действия двух сил пересекаются, то их равнодействующая есть диагональ параллелограмма, построенного на этих силах, как на сторонах.
Величина равнодействующей при этом определяется по теореме косинусов:
R F1 F2
R 
 F12 F22 2F1F2 cos(1800 )
F12 F22 2F1F2 cos(1800 )

 F12 F22 2F1F2 cos ;
F12 F22 2F1F2 cos ;
Рис.3.6.
Направление равнодействующей может быть определено по теореме синусов:
F1 F2 |
R |
|
|
|
|
|
sin |
sin |
sin . |
Аксиома параллелограмма сил |
|||
|
|
F3 |
||||
|
F1 |
дает |
возможность |
найти |
||
|
R |
|||||
|
|
равнодействующую |
нескольких сил, |
|||
|
|
|
приложенных к телу. Для этого |
|||
|
|
R=F1+F2+F3 |
необходимо сложить последовательно |
|||
|
|
вектора |
сил |
по |
правилу |
|
|
F2 |
|
параллелограмма (рис. 3.7). |
|
||
|
Рис.3.7. |
|
|
|
|
|
|
|
|
|
|
|
|
Аксиома равенства действия и противодействия (рис. 3.8): всякому механическому |
||||||
действию всегда есть равное и противоположно направленное противодействие. |
|
|||||
|
|
Эту аксиому следует понимать в такой трактовке: если |
||||
|
F |
тело A действует на тело B с некоторой силой FA B , то тело B |
||||
A |
B-A |
в свою очередь действует на тело A с силой FВ А FA B . По |
||||
|
||||||
|
|
|||||
B |
FB-A=-FA-B сути, аксиома |
равенства действия и |
противодействия |
|||
|
представляет собой 3-й закон Ньютона. |
|
|
|||
|
FA-B |
Следует |
заметить, что |
сила действия FA B |
и сила |
|
|
противодействия FВ А не являются системой сил, поскольку |
|||||
|
|
они приложены к разным телам. |
|
|
|
|
Рис.3.8.
Аксиома затвердевания: если деформируемое тело под действием системы сил находится в равновесии, то последнее не изменится, если тело затвердеет.
